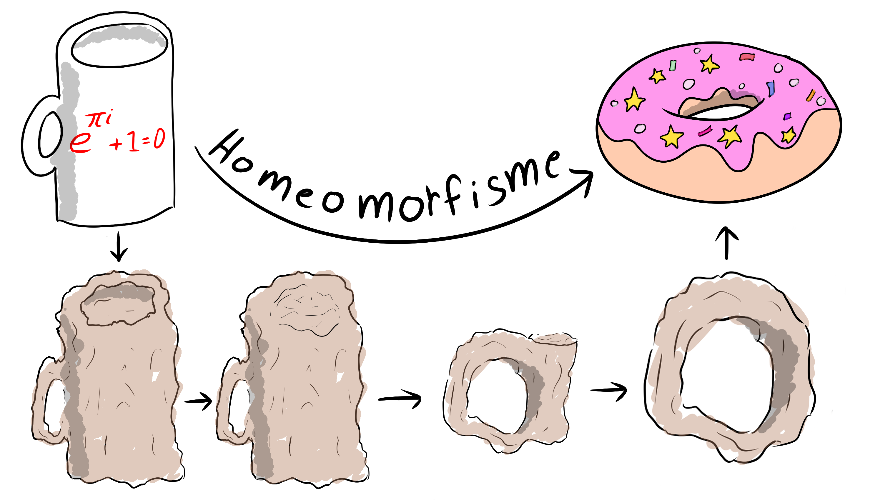
Mok = donut
Misschien heb je het wel eens gehoord, dat een mok en donut 'hetzelfde' zijn. Maar wat is dat voor iets geks? Zelf zou ik nooit mijn koffie uit een donut drinken of een hap nemen van een koffiemok. Volgens de topologie, een deelgebied van de wiskunde, is het toch zo. In dit artikel gaan we daar eens naar kijken, wanneer zijn objecten nou precies gelijk en waarom?
Stel dat een mok van deeg is gemaakt, dan kunnen we de koffiemok wel omkneden tot een donut. Dit omvormen van objecten en kijken of ze gelijk zijn is wat veel wordt bestudeerd binnen het deelgebied van wiskunde genaamd topologie, de studie van ruimten en vormen. Allereerst gaan we in op solide (vaste) objecten met inhoud, zoals de koffiemok en de donut. Als we willen weten waarom een koffiemok en een donut 'gelijk' zijn, moeten we eerst weten wanneer we solide objecten als gelijk beschouwen. Binnen de topologie hebben we zelf een naam voor het gelijk zijn van objecten: homeomorf, homeo voor 'gelijk' en morf voor 'vorm'. Topologen beschouwen twee solide objecten als gelijk indien er een zogenaamd homeomorfisme tussen de objecten bestaan. Vanaf nu schrijven we 'gelijk' als we deze topologische versie bedoelen. Maar wat is dan een homeomorfisme? Een formele definitie gaat hier te ver, maar we kunnen hier wel intuïtief een begrip over krijgen en dat zal grof gezegd overeenkomen met de formele definitie. Voor onze intuïtieve definitie is het zelfs genoeg om objecten na te maken van klei en om vervolgens te kijken of ze ' netjes' in elkaar om te kneden zijn. Voor het netjes kneden zijn afspraken nodig over wat wel en wat niet mag tijdens het kneden. De regels van het kneden luiden als volgt:
- Tijdens het kneden mogen er geen gaten worden toegevoegd.
- Tijdens het kneden mogen er geen gaten worden verwijderd.
- Het object moet tijdens het kneden één geheel blijven.
Een homeomorfisme is nu intuïtief te begrijpen als een kneding volgens de bovenstaande regels. Zo zou een voorbeeld kunnen zijn dat je een bol van klei op zes vlakken platdrukt om een kubus te vormen. Die kneding is volgens de regels omdat er geen gaten worden toegevoegd of verwijderd en het object één geheel blijft. Dan spreken we over een homeomorfisme tussen een bol en een kubus en dus zijn ze homeomorf of gelijk. (Je zou dan ook kunnen beargumenteren dat wiskundigen geen onderscheid kunnen maken tussen dobbelstenen en biljartballen, test dat maar eens op de biljarttafel!) Een homeomorfisme tussen twee objecten kunnen we dus zien als een continue vervorming tussen die twee objecten.
Hoe kunnen we nu zien dat een mok en een donut gelijk zijn? Wel, laten we die objecten eens namaken van klei en zien of ze in elkaar om te kneden zijn, zie figuur 1. Wellicht denk je dat deze kneding niet volgens de bovenstaande regels is, immers vullen we de ruimte op waar normaal koffie in zit. Deze ruimte is echter geen gat omdat het slechts één opening heeft. We kunnen de bodem van de mok zo dik maken dat deze tot de rand van de mok komt en dan is er niet eens een holle ruimte. Als er aan de onderkant van de mok wel een opening had gezeten, dan was deze opvulling niet mogelijk omdat de openingen aan de boven- en onderkant van de mok nu samen een gat door de mok vormen, en die mag volgens de regels niet worden verwijderd.
Oppervlakken
Laten we nu eens kijken naar een ander soort object: oppervlakken. Anders dan solide objecten met inhoud, hebben deze objecten geen inhoud. In de wiskunde zijn ze zelfs oneindig dun, maar een goede voorstelling uit het echte leven kan een ballon zijn. Ze zijn ook wel voor te stellen als de 'buitenkanten' van solide objecten.
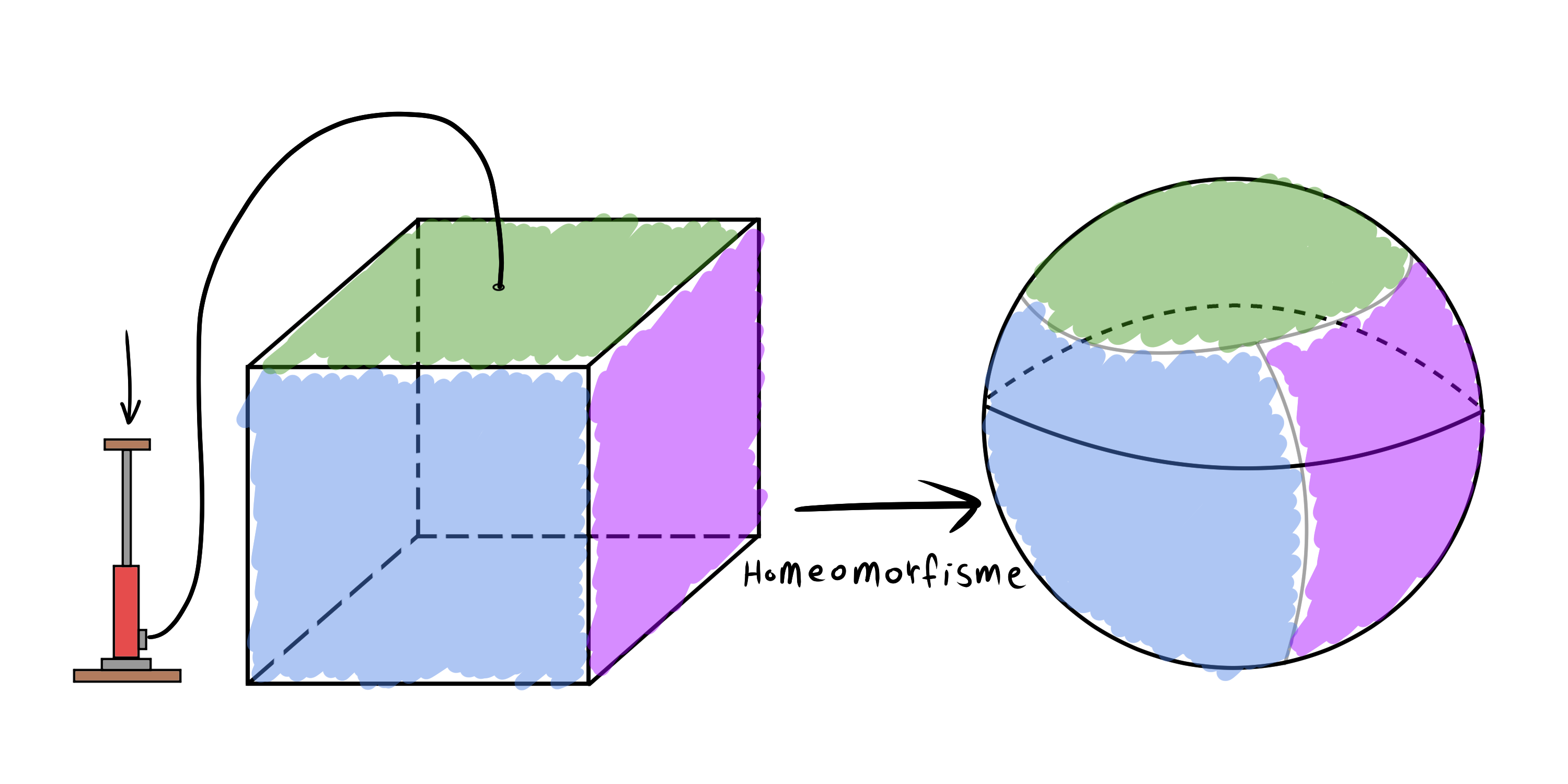
Zoals bij de solide objecten met inhoud is het interessant om te zien wanneer oppervlakken gelijk zijn. Hier is kneden natuurlijk een stuk moeilijker, maar het begrip blijft min of meer hetzelfde: als we twee oppervlakken op continue wijze in elkaar kunnen omvormen, dan zijn ze grof gezegd homeomorf. Een voorbeeld kan zijn dat we de buitenkant van een kubus hebben. Als we die nu extra opblazen zoals een ballon, dan kunnen we voorstellen dat de vlakken van de kubus zo bol krommen dat we uiteindelijk een sfeer krijgen (een sfeer is de buitenkant van een bol, dus zoals de schil van een mandarijn, maar dan oneindig dun), zie figuur 2. En inderdaad,
ook formeel zijn de buitenkant van een kubus en een sfeer homeomorf!
Maar voor oppervlakken is er ook een andere manier om ze te vergelijken. We kunnen namelijk voor oppervlakken een zeker getal berekenen, de zogenaamde Eulerkarakteristiek. Dat is een getal dat een zekere essentie van het oppervlak weergeeft en later zullen we ook zien dat dit getal in relatie staat met een aantal belangrijke eigenschappen van oppervlakken, zoals het aantal gaten van een oppervlak. Oppervlakken vergelijken op basis van de Eulerkarakteristiek is wel iets zwakker dan het homeomorf zijn van twee oppervlakken: twee oppervlakken kunnen dezelfde Eulerkarakteristiek hebben maar hoeven dan niet per se homeomorf te zijn. Omgekeerd geldt wel dat homeomorfe oppervlakken dezelfde Eulerkarakteristiek hebben. Maar hoe berekenen we de Eulerkarakteristiek van een oppervlak? Wederom kunnen we gebruikmaken van onze handvaardigheid, we kunnen de Eulerkarakteristiek namelijk berekenen door driehoeken op een oppervlak te tekenen. Dit heet ook wel het trianguleren van een oppervlak. Maar ook hier moeten we werken volgens een aantal regels: Verschillende zijden van driehoeken mogen elkaar enkel snijden op de hoekpunten van de driehoeken. Wel kunnen verschillende driehoeken overeenkomstige zijden hebben. De driehoeken moeten het gehele oppervlak overdekken.
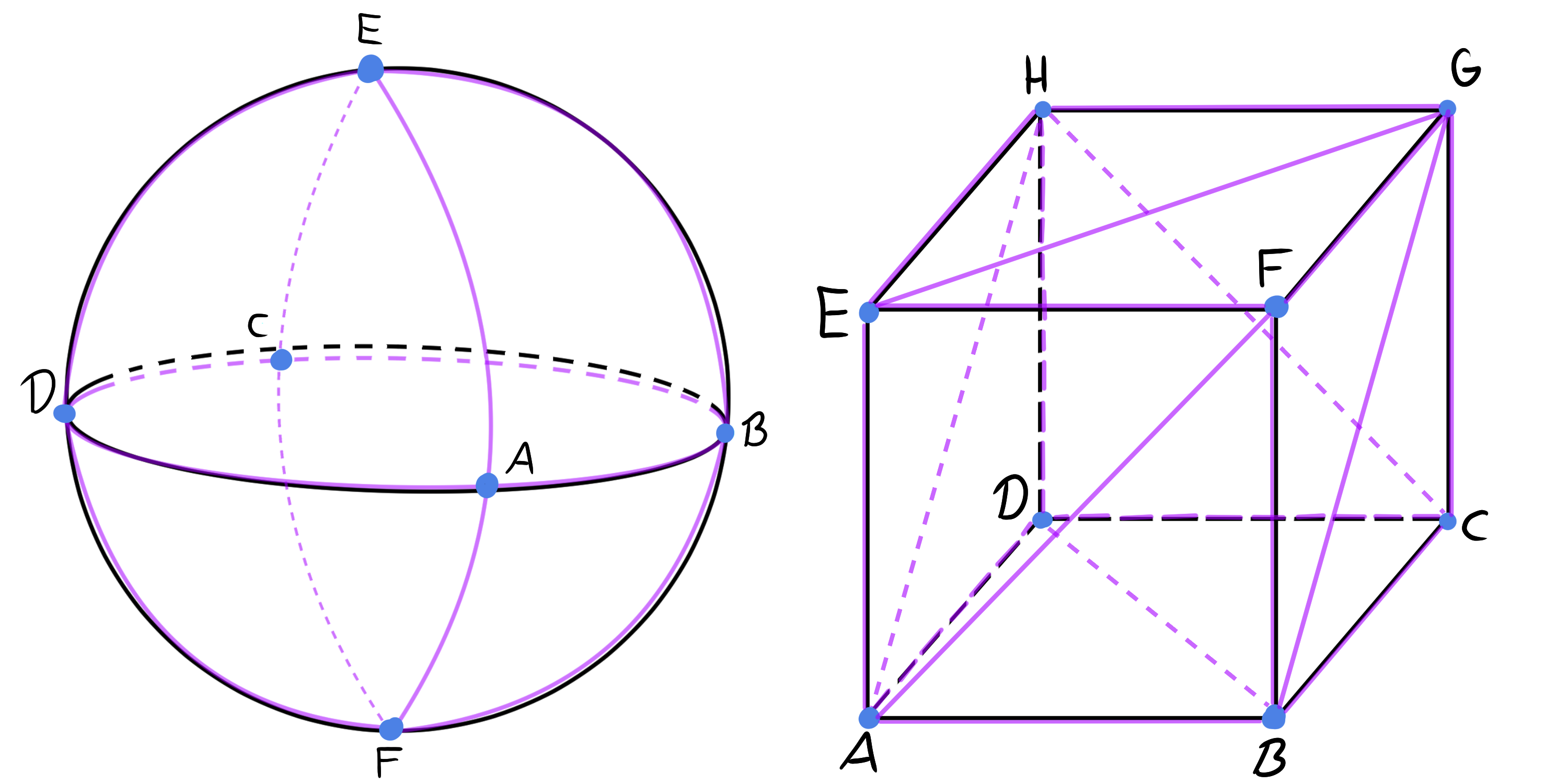
Zie figuur 3 voor een voorbeeld van triangulaties op de buitenkant van een kubus en op een sfeer.
Nadat we klaar zijn met tekenen is het tellen geslagen. We moeten het aantal hoekpunten, het aantal zijden en het aantal vlakken van de triangulatie tellen. Algemeen zullen we de verzameling hoekpunten noteren als $P$, de verzameling zijden als $Z$ en de verzameling vlakken als $V$. Het aantal elementen in de verzameling hoekpunten zullen we noteren als $|P|$ en evenzo noteren we $|Z|$ en $|V|$ voor het aantal zijden en vlakken respectievelijk. Als we een oppervlak algemeen de naam $M$ geven, dan noteren we de Eulerkarakteristiek van $M$ als $\chi(M)$. De Eulerkarakteristiek $M$ kunnen we dan berekenen als
$$\chi(M) = |P| - |Z| + |V|.$$
Nu komt wellicht nog de vraag naar boven: welke triangulatie moet ik tekenen? Mag ik gewoon volgens de regels maar wat driehoeken op een oppervlak tekenen en dan op de bovenstaande manier de Eulerkarakteristiek berekenen? Het antwoord: ja dat mag! De Eulerkarakteristiek is onafhankelijk van de triangulatie. Dus zolang je op een gegeven oppervlak een triangulatie tekent volgens de regels, zal je uiteindelijk altijd uitkomen op dezelfde Eulerkarakteristiek. Probeer dit zelf eens na te gaan door in een triangulatie een driehoek toe te voegen (deel bijvoorbeeld een driehoek doormidden door op een zijde een punt toe te voegen en tussen dat punt en het tegenoverliggende punt in de driehoek een zijde toe te voegen, dan blijft de waarde van $|P| - |Z| + |V|$ gelijk.)
Laten we nu maar een voorbeeld bekijken waarin we de Eulerkarakteristiek van de buitenkant van een kubus en van een sfeer bepalen. Eerder hebben we gezien dat de buitenkant van een kubus en een sfeer homeomorf zijn, dus zoals eerder gezegd moet dan ook wel gelden dat ze dezelfde Eulerkarakteristiek hebben. Dat kunnen we direct controleren door de Eulerkarakteristiek van beide oppervlakken te berekenen. We gebruiken de triangulaties van figuur 3.
Voor beide oppervlakken moeten we de verzamelingen $P$, $Z$ en $V$ van hoekpunten, zijden en vlakken bepalen. Voor de sfeer hebben we
$$
\begin{align*}
P_{\rm sfeer} &= \{A,B,C,D,E,F\}\\
Z_{\rm sfeer} &= \{AB,BC,CD,AD,AE,BE,CE,DE,AF,BF,CF,DF\}\\
V_{\rm sfeer} &= \{\Delta ABE, \Delta BCD, \Delta CDE, \Delta ADE, \Delta ABF, \Delta BCF, \Delta CDF, \Delta ADF\}
\end{align*}
$$
en voor de buitenkant van de kubus hebben we
$$
\begin{align*}
P_{\rm kubus} &= \{A, B, C, D, E, F, G, H\}\\
Z_{\rm kubus} &= \{AB,BC,CD,AD,BF,CG,DH,AE,EF,FG,GH,HE,BD,AF,BG,CH,AH,EG\}\\
V_{\rm kubus} &= \{\Delta ABD, \Delta BCD, \Delta ABF, \Delta AEF, \Delta BCG, \Delta BFG, \Delta CDH, \Delta CGH, \Delta ADH, \Delta AEH, \Delta EFG, \Delta EGH\}
\end{align*}
$$
Nu kunnen we voor beide oppervlakken de Eulerkarakteristiek berekenen. Door simpelweg te tellen vinden we dat de verzameling $P_{\rm sfeer}$ van punten op de sfeer in totaal $6$ punten bevat, dus we hebben dat $|P_{\rm sfeer}| = 6$. Evenzo vinden we dat $|Z_{\rm sfeer}| = 12$ en $|V_{\rm sfeer}| = 8$ en dus krijgen we dat
$$\chi({\rm sfeer}) = |P_{\rm sfeer}| - |Z_{\rm sfeer}| + |V_{\rm sfeer}| = 6 - 12 + 8 = 2.$$
Bij de kubus vinden we na grondig tellen dat $|P_{\rm kubus}| = 8$, $|Z_{\rm kubus}| = 18$ en $|V_{\rm kubus}| = 12$ dus
$$\chi({\rm kubus}) = 8 - 18 + 12 = 2.$$
Zo zien we dat zowel de sfeer als de kubus Eulerkarakteristiek $2$ hebben. Ze hebben dus inderdaad dezelfde Eulerkarakteristiek!
Eulerkarakteristiek en aantal gaten
Zoals eerder gezegd zijn er een aantal belangrijke eigenschappen van oppervlakken gerelateerd aan de Eulerkarakteristiek. Laten we eens kijken hoe de Eulerkarakteristiek verbonden is met het aantal gaten in een oppervlak, ook wel het genus van een oppervlak. Om geen verwarring te creëren over wat 'gaten' precies zijn, zullen we enkel naar zogenaamde gesloten oppervlakken kijken. Dit zijn oppervlakken die een stuk lucht insluiten en waaruit de lucht dan niet kan ontsnappen, je mag ook wel denken aan ballonnen. Zoiets als een sfeer, de buitenkant van een kubus of de buitenkant van een donut mogen dus wel, maar zoiets als een vel papier niet.
Maar wat bedoelen we dan met 'gaten' in oppervlakken? Nou niet het soort gaten die zorgen dat je ballon leegloopt. Nee, we bedoelen gaten die worden 'omringd' door het oppervlak. Denk maar aan een ballon in de vorm van een donut: dit oppervlak omringt het gat van de donut. Zo'n donut ballon heeft slechts één gat dus dan zeggen we dat dit oppervlak genus $1$ heeft. Zie figuur 4 voor andere voorbeelden van gesloten oppervlakken met gaten.
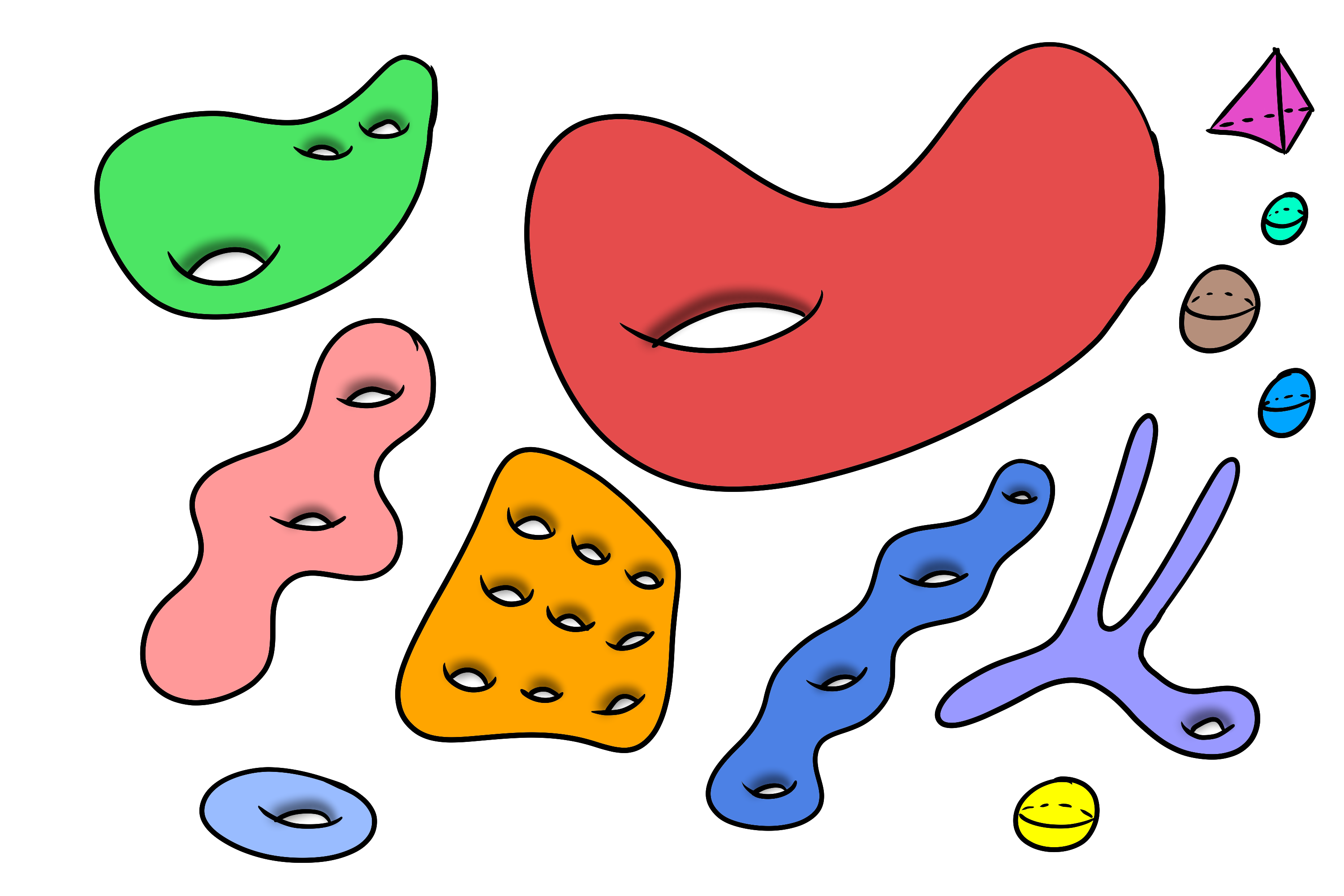
Hoe is het aantal gaten in een gesloten oppervlak, het genus dus, nu gerelateerd aan de Eulerkarakteristiek van een oppervlak? Als we het genus van een oppervlak $M$ noteren als $g(M)$, dan geeft de volgende formule de relatie tussen de genus $g(M)$ en de Eulerkarakteristiek $\chi(M)$:
$$\chi(M) = 2 - 2g(M).$$
Het handige aan deze formule is dat het veel makkelijker wordt om de Eulerkarakteristiek van een oppervlak te berekenen. We hoeven een oppervlak nu niet te trianguleren en vervolgens alle punten, zijden en vlakken tellen. We kunnen simpelweg het aantal gaten tellen. Zo heeft een sfeer $0$ gaten dus $g({\rm sfeer}) = 0$ en dat geeft $\chi({\rm sfeer}) = 2 - 2 \cdot 0 = 2$, precies zoals we eerder hebben gevonden. Andersom kunnen we voor een oppervlak waarbij we niet zeker zijn over de genus ook de Eulerkarakteristiek bepalen en vervolgens de genus berekenen met de formule. Laten we met deze formule eens controleren dat de buitenkant van een donut als oppervlak precies één gat heeft. Eerst trianguleren we de buitenkant van de donut (zie figuur 5).
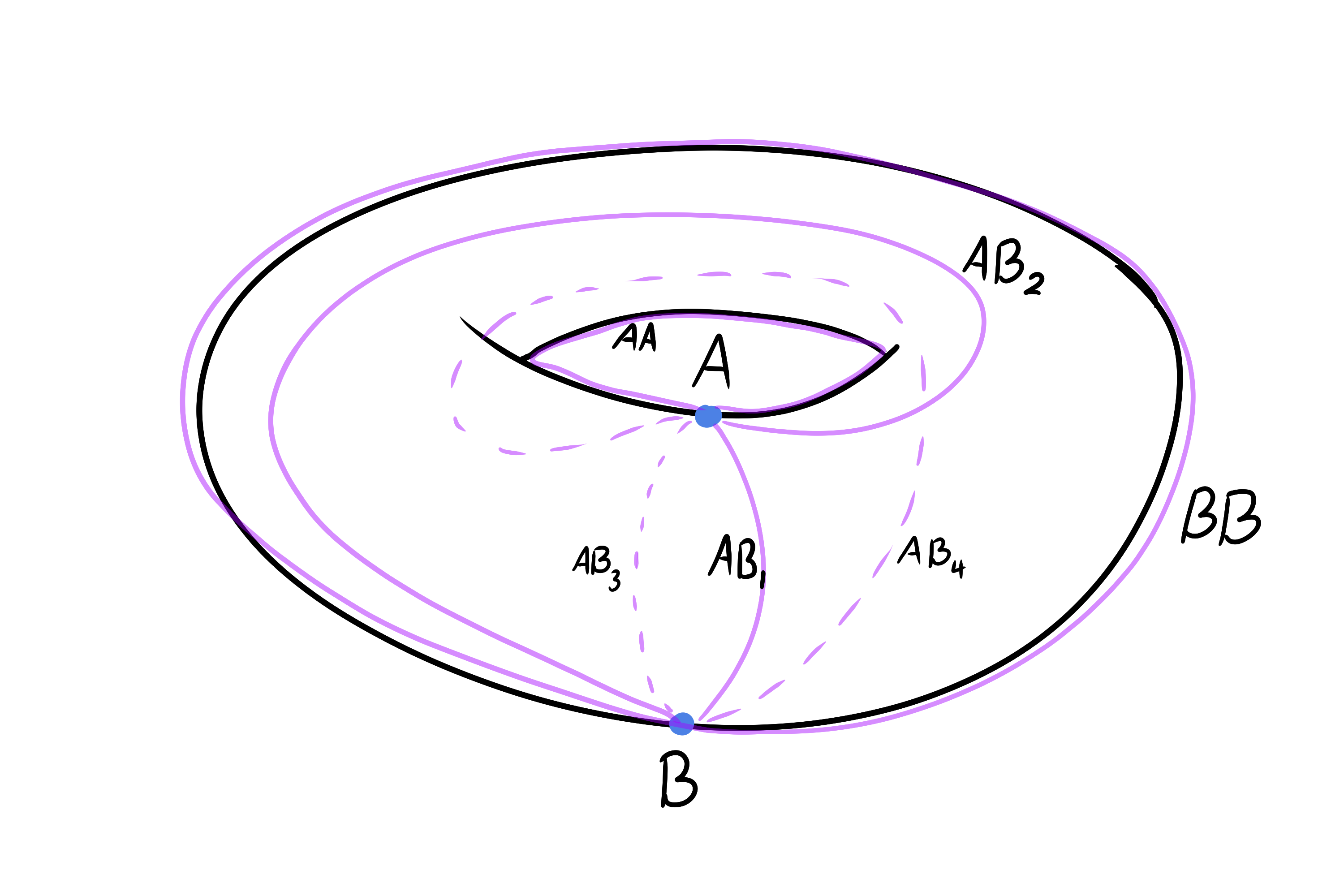
Wellicht lijkt dit een wat vreemde triangulatie omdat we geen standaard 'driehoeken' zien. Op zowel de bovenkant als de onderkant van de donut hebben we nu echter twee driehoeken, de zijden zijn gewoon zeer gekromd. Omdat we nu meerdere zijden tussen dezelfde punten hebben, moeten we verschillende zijden tussen hetzelfde paar punten nummeren en we kunnen driehoeken nu niet meer enkel noteren door aan te geven wat de hoekpunten zijn. We gebruiken voor bijvoorbeeld de driehoek met zijden $AB_1$, $AB_2$ en $AA$ de notatie $\Delta[AB_1, AB_2, AA]$. We hebben dan de volgende verzamelingen
$$
\begin{align*}
P &= \{A, B\}\\
Z &= \{AA,AB_1,AB_2,AB_3,AB_4,BB\}\\
D &= \{\Delta AB_1[AB_1, AB_2, AA], \Delta[AB_1, AB_2, BB], \Delta[AB_3, AB_4, AA], \Delta[AB_3, AB_4, BB]\}
\end{align*}
$$
Hier hebben we dus $2$ punten, $6$ zijden en $4$ driehoeken dus volgt nu
$$\chi({\rm donut}) = |P| - |Z| + |D| = 2 - 6 + 4 = 0.$$
Nu geeft de formule dat $0 = 2 - 2g({\rm donut})$ en oplossen voor $g({\rm donut})$ geeft dan $g({\rm donut}) = 1$. Mocht je dus nog niet zeker zijn dat de buitenkant van een donut als oppervlak één gat heeft, dan weet je nu in ieder geval hoe je dat wiskundig na kunt gaan.
