Op 14 juli overleed Maryam Mirzakhani, een van ’s werelds beste wiskundigen en vooralsnog de enige vrouwelijke winnaar van de Fieldsmedaille, een soort Oscar voor wiskundigen. Mirzakhani kwam uit Iran, maar woonde en werkte sinds haar promo-tietijd in de Verenigde Staten.

Als scholier in Teheran wilde ze aanvankelijk schrijver worden, maar gaandeweg genoot ze steeds meer van wiskunde, waar ze veel talent voor had. In 1994 en 1995 deed ze mee aan de Internationale Wiskunde Olympiade. In 1995 haalde ze de maximale score van 42 punten, in 1994 had ze maar één punt minder. Met twee gouden medailles op zak was duidelijk dat ze in dit vak verder wilde.

Sinds 2008 was Mirzakhani hoogleraar aan de universiteit van Stanford. Ze overleed deze zomer aan borstkanker, slechts veertig jaar oud. ‘Een schitterend brein, een schitterende ziel, een prachtige vrouw. Een boegbeeld voor Iran en voor vrouwen in de wetenschap’, twitterde de Franse wiskundige, Fields-winnaar én kersverse politicus Cédric Villani.

Mirzakhani’s onderzoek ging over het begrijpen van structuren op oppervlakken. Bijvoorbeeld: welk patroon maakt een eeuwig kaatsende biljartbal op het laken van een biljarttafel? Soms is het een repeterend patroon. Bijvoorbeeld als je de bal loodrecht tegen een van de zijkanten van de rechthoekige biljarttafel kaatst. 

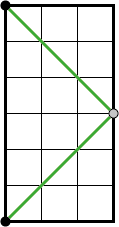
De bal beweegt dan eeuwig heen en weer in één rechte lijn. Maar als de bal onder een andere hoek tegen een zijkant wordt gekaatst, wat dan? Kan het resulterende patroon de hele tafel bedekken? In welke gevallen komt de bal na een zeker aantal weerkaatsingen weer terecht op het beginpunt? En hoe zit het als de tafel niet rechthoekig is, maar driehoekig, of vijfhoekig, of een of andere bizarre vorm heeft?

Samen met haar collega Alex Eskin van de universiteit van Chicago deed Mirzakhani baanbrekend onderzoek naar het patroon dat een biljartbal op gecompliceerde vormen tekent. Dat onderzoek is nog lang niet voltooid, want in zijn algemeenheid is dit nog altijd een open vraag. 

Mirzakhani’s wiskunde is veel te moeilijk voor dit tijdschrift (en voor de auteur van dit stukje), maar als eerbetoon geven we hier een biljartpuzzel waar elke wiskundeliefhebber plezier in kan hebben.

ReChthOekIg, 45 graden

Stel je een recht-hoekige biljarttafel voor, met een gat in elk van de vier hoeken. Vanuit de hoek linksonder stoot je een bal weg onder een hoek van 45°. Belandt de bal ooit in een gat? Zo ja, na hoeveel botsingen?

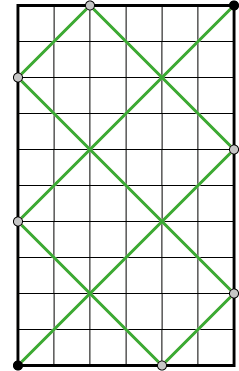
In figuur 1 en 2 zie je twee voorbeelden: biljarttafels van \(3 \times 6\) en van \(6 \times 10\). Het aantal botsingen totdat de bal in een gat belandt, is hier \(2\) respectievelijk \(7\). (Als de bal in een gat verdwijnt, tellen we dat mee als een botsing.) Omdat een tafel van \(1 \times 2\) niet wezenlijk anders is dan een tafel van \(3 \times 6\), en \(3 \times 5\) niet anders dan \(6 \times 10\), nemen we vanaf nu aan dat \(a\) en \(b\), de afmetingen van de tafel, geen gemeenschappelijke delers hebben. We gaan dus uit van een biljarttafel van \(a \times b\) waarbij \(a\) en \(b\) gehele getallen zijn waarvan de grootste gemeenschappelijke deler gelijk is aan \(1\). 

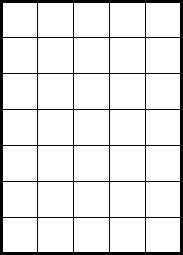
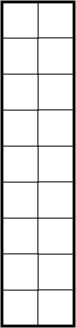
Teken zelf op de tafels van figuur 3 \((5 \times 7)\) en 4 \((2 \times 9)\) het patroon dat de biljartbal maakt. Na hoeveel botsingen belandt de bal in een gat? Kun je een algemene stelling formuleren (en bewijzen) voor het aantal botsingen totdat de bal in een gat verdwijnt? Als dat je lukt, kun je – zonder het patroon uit te tekenen – beantwoorden wat er gebeurt op een tafel van \(2017 \times 2018\). 

Het verhaal gaat verder onder de knop "Bekijk oplossing"

Bekijk oplossing