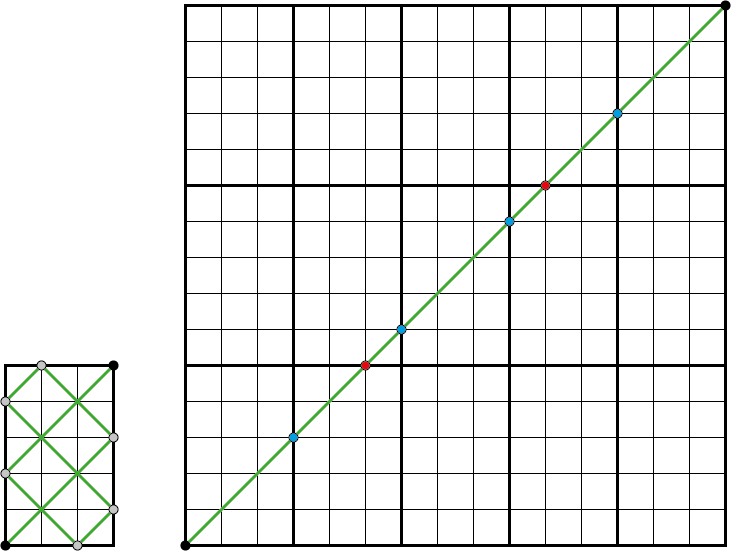
De truc is om \(a \cdot b\) kopieën van de biljarttafel zó tegen elkaar te leggen, dat een vierkant ontstaat. In figuur 5 zie je dit voor een tafel van \(3 \times 5\). De weg die de bal aflegt, is de diagonaal van het vierkant van linksonder naar rechtsboven. De bal passeert hierbij \(15\) (in het algemeen: \(a \cdot b\)) hokjes. De bal doorsnijdt \(2\) (algemeen: \(a - 1\)) keer een horizontale lijn (begin- en eindpunt niet meegerekend): dit zijn de rode punten. En de bal doorsnijdt \(4\) (algemeen: \(b - 1\)) keer een verticale lijn (begin- en eindpunt niet meegerekend): de blauwe punten. Het totale aantal botsingen komt hiermee op \(2 + 4 + 1 = 7\). De laatste ‘plus 1’ is nodig vanwege onze afspraak dat de laatste beweging van de bal, waarna die in een gat verdwijnt, ook als botsing meetelt.

We hebben nu de volgende stelling bewezen:

Gegeven is een biljarttafel van \(a \times b\), met \(\mbox{ggd}(a,b)=1\). Als je een bal vanuit de hoek linksonder weg stoot onder een hoek van 45°, dan belandt de bal bij botsing \(a+b-1\)in een gat.

De eis dat de grootste gemene deler van \(a\) en \(b\) gelijk is aan \(1\), is nodig, want anders komt de bal al eerder dan na \(a+b-1\)botsingen in een gat.

Met onze stelling is het een fluitje van een cent om te berekenen na hoeveel botsingen de bal zijn weg heeft voltooid als de tafel de afmeting \(2017 \times 2018\) heeft: \(2017+2018–1=4034\).

Tot slot: kun je zelf bedenken waarom de volgende drie beweringen waar zijn?

• Als \(a\) en \(b\) oneven zijn, eindigt de bal in de rechter bovenhoek.
• Als \(a\) even is en \(b\) oneven, eindigt de bal in de rechter benedenhoek.
• Als \(a\) oneven is en \(b\) even, eindigt de bal in de linker bovenhoek.

Het geval waarbij zowel \(a\) als \(b\) even is doet zich niet voor, want dan is de grootste gemene deler van \(a\) en \(b\) groter dan \(1\). Als \(a\) en \(b\) geen gehele getallen zijn, maar breuken, kun je de biljarttafel zodanig vergroten, dat de afmetingen geheel worden. En als \(a\) en \(b\) irrationaal zijn? Tja, dan wordt het in één klap ontzettend veel moeilijker. Om aan een tafel van \(\pi \times e\) te rekenen, moet je misschien wel Mirzakhani heten…