Milli en Mu hebben heerlijk Hex en Chomp gespeeld. Jij ook? Ze snapten echter nog niet hoe je bepaalt wie kan winnen en, belangrijker nog, hoe die persoon kan winnen. Maar het zat hen vooral dwars dat Phi en Pi het met elkaar oneens waren of die spellen nu waren opgelost of niet. De een zei dat Hex wel was opgelost en ander van niet. En bij Chomp was het net zo. Toen dat weer eens ter sprake kwam tijdens het avondeten, probeerden hun ouders het uit te leggen. Milli en Mu hadden nu beiden op school geleerd over wortels en machtsverheffen en dat een getal als $\sqrt{2} = 2\tfrac{1}{2}$ geen breuk is, dat wil zeggen niet geschreven kan worden als $\frac{p}{q}$ voor gehele getallen $p$ en $q$. Zulke getallen heten irrationaal: niet te schrijven als een ratio (verhouding).

		Voor de oude Grieken waren gehele getallen en rationale getallen bijna heilig. Zo klinken twee tonen mooi samen als hun snaarlengtes een verhouding van twee gehele getallen hebben: de verhouding $1:2$ geeft een octaaf en $2:3$ een reine kwint.

"Kijk," zei Phi, "laten we Hex en Chomp even vergeten. Hier is een klassiek probleempje: Bestaan er irrationale getallen $a$ en $b$ zodanig dat $a^b$ rationaal is, dus wel te schrijven is als een breuk?" Pi beweerde daarop dat dit probleem pas rond 1934 echt is opgelost, terwijl Phi zei dat het zelfs daarvoor al was opgelost. Dat moesten Milli en Mu even laten bezinken. Maar ze kwamen er niet uit. "Nou," vervolgde Phi, "je moet om te beginnen de vraag goed lezen. Er wordt alleen gevraagd of zulke irrationale getallen $a$ en $b$ bestaan en niet om zulke getallen ook daadwerkelijk te vinden. Beschouw het getal . Er zijn nu twee mogelijkheden: $c$ is rationaal of irrationaal. In het eerste geval is het probleem, per definitie, opgelost door $a = b = \sqrt{2}$, die beide irrationaal zijn, want dan geldt $a^b = c$ waarvan aangenomen was dat het een rationaal getal is. En in het tweede geval is het opgelost door $a = c$ en $b = \sqrt{2}$, die dan beide irrationaal zijn." We kunnen narekenen dat $a^b$ in dat geval rationaal is. Reken maar mee:

$$a^b=c^{\sqrt{2}}=\left(\sqrt{2}^{\sqrt{2}}\right)^{\sqrt{2}}=\sqrt{2}^{\sqrt{2}\cdot\sqrt{2}}=\sqrt{2}^2=2.$$

Dus inderdaad geldt nu dat $a^b$ rationaal is (zelfs geheel).

Daarmee is het probleem van het bestaan van zulke getallen opgelost. "Aha," zei Milli, "nu zie ik het." Maar Mu had daar nog wat moeite mee: "Wat zie je dan?" "Nou, dat er nog steeds iets niet is opgelost, namelijk voor welke getallen $a$ en $b$ nu geldt dat ab irrationaal is."

"Dat klopt," zei Pi, "en dat is pas in 1934 echt opgelost, namelijk met de Stelling van Gelfond–Schneider, waaruit volgt dat $c$ irrationaal is."

Tja, en wat heeft dat nou met Hex en Chomp te maken? Hier moeten Milli en Mu even over nadenken. Al snel valt het kwartje: of je kan winnen betekent dat er een zet bestaat waarmee je kan winnen.

Weten hoe je kan winnen vereist dat je die zet ook daadwerkelijk kunt vinden. Dus wat Phi en Pi beweren is dat we wel weten wie er in de beginsituatie kan winnen, maar in het algemeen niet hoe dat dan moet. Hoe zit dat met Hex? Hieronder zie je nogmaals een Hex bord. De twee spelers zetten om de beurt een steen van hun eigen kleur in een leeg vakje. Wie als eerste de twee (overliggende) eigen zijden verbindt met een ononderbroken pad, die wint. In Pythagoras 63-5 werd al vermeld dat er geen remise mogelijk is.

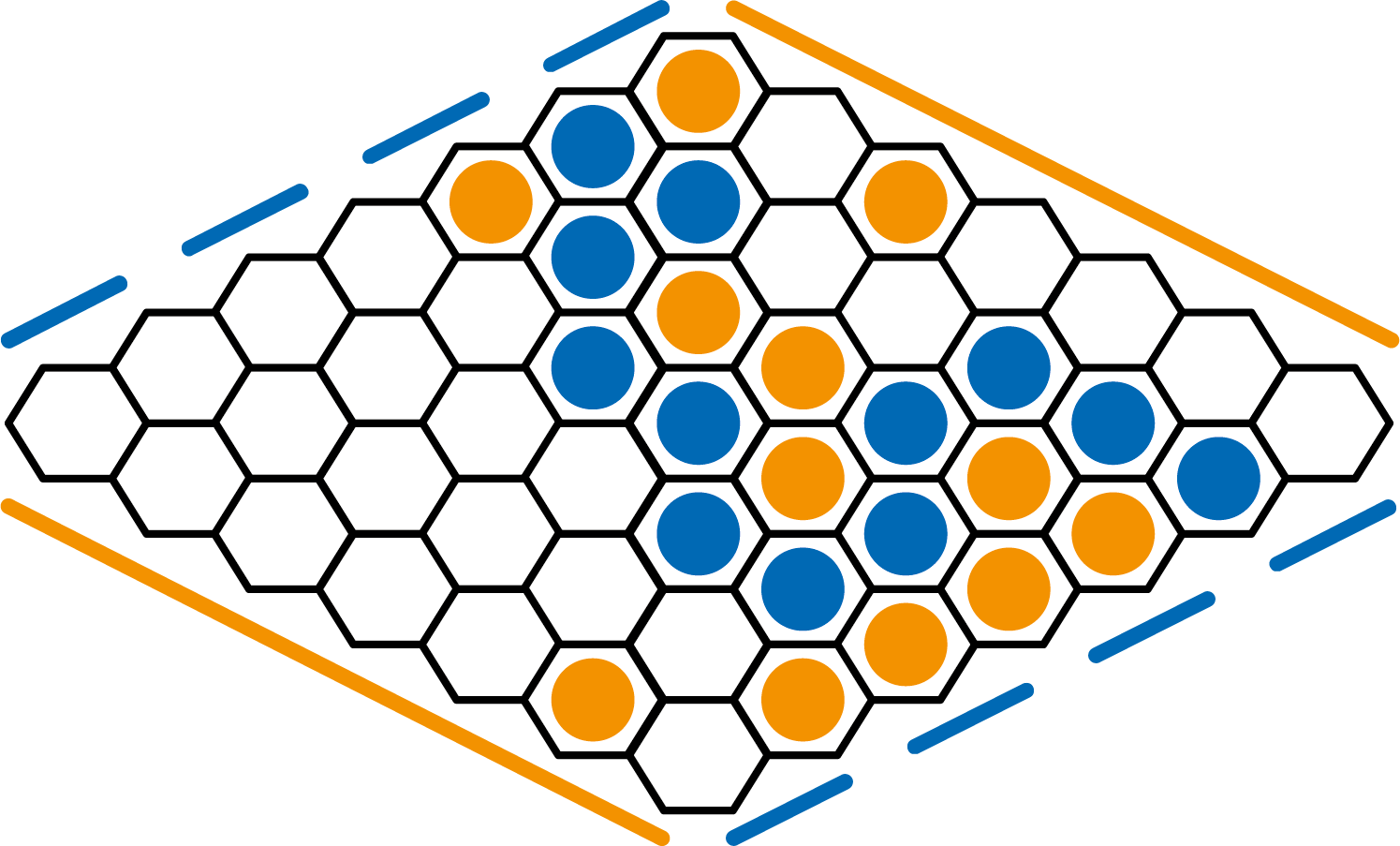
Stel dat de tweede speler, genaamd T, een winnende strategie heeft. We gaan laten zien dat dit tot een tegenspraak leidt. Daarmee hebben we dan aangetoond dat de eerste speler altijd kan winnen. De eerste speler, genaamd E, gaat als volgt te werk. In gedachte zet E ergens een steen van T op het bord; dat vakje, zeg V, blijft dus in werkelijkheid leeg. Vervolgens past E, in gedachte, de winnende strategie voor tweede spelers toe om een eigen (winnende) zet te bepalen en voert die uit. E blijft bij elke zet die winnende strategie volgen (met in gedachten dus een steen van T in vakje V). Daarbij zal E nooit in het vakje V spelen. Mocht T dat wel doen, dan is er niks aan de hand, want E deed toch al alsof daar een steen van T stond. Uiteindelijk wint E. Dit is in tegenspraak met de aanname dat T kon winnen. En als E niet wint, dan klopte de strategie die E volgde niet, wat ook in tegenspraak is met de aanname. Daarmee weten we de dus wel dat de eerste speler op elke bordgrootte kan winnen, maar we weten nog niet hoe.

Deze bewijstechniek heet in het Engels strategy stealing. Van Hex weten we ondertussen door middel van computeranalyses ook hoe de eerste speler kan winnen op borden tot en met $9\times9$. Er blijken vele winnende eerste zetten te zijn.

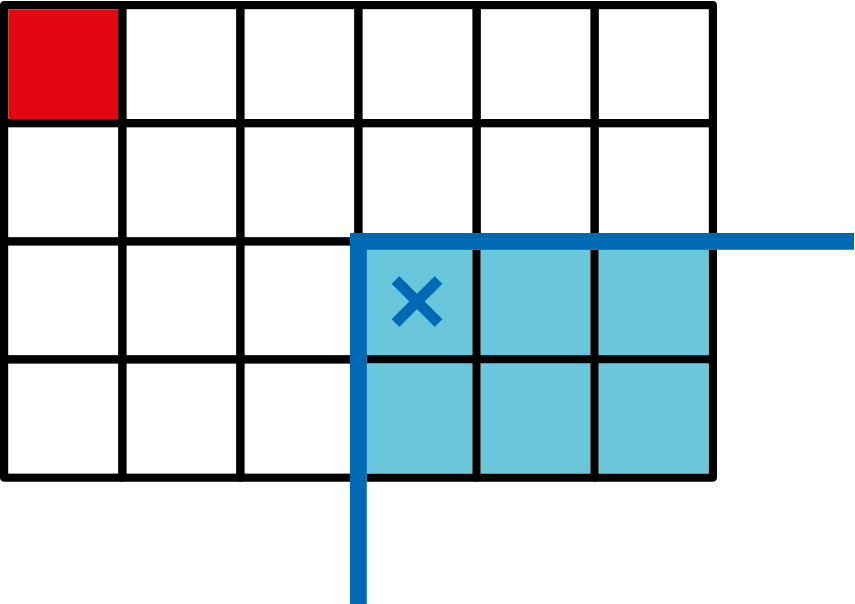
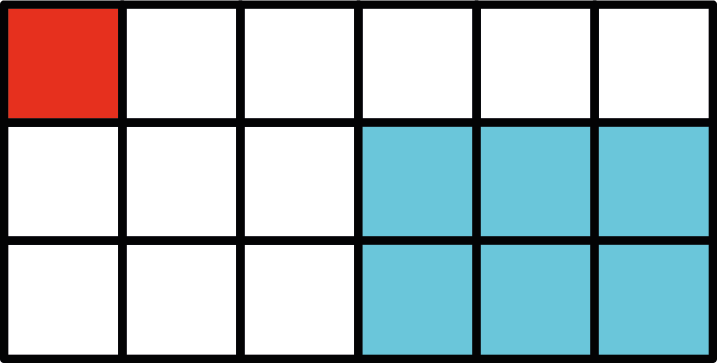
Voor Chomp is het zelfs nog makkelijker in te zien dat de eerste speler kan winnen. Hieronder staat de beginstand van Chomp met een $4\times6$ blok chocolade, waarbij de eerste zet wordt gedaan door blokje $\color{navy}{\times}$ met alles rechtsonder ervan weg te pakken. Spelers pakken zo om de beurt één of meer blokjes weg. Wie het rode blokje linksboven pakt, die verliest.

Stel dat de tweede speler (T) een winnende strategie heeft. Dat wil zeggen dat T op elke zet van de eerste speler (E) een winnend antwoord heeft. Wat E nu doet is het volgende. In gedachte pakt E als eerste zet alleen het ene blokje rechtsonder. Vervolgens past E de winnende strategie voor tweede spelers toe. Deze zet hapt een stuk weg dat je ook altijd meteen met de eerste zet had kunnen wegnemen. Dit is dan de zet waarmee E begint. Of E nu wint of verliest, in beide gevallen is dat in tegenspraak met de aanname dat de tweede speler een winnende strategie heeft. Merk op dat ook bij Chomp remise onmogelijk is.

Alweer werkt strategy stealing.

Uiteraard is met de computer uitgezocht hoe het zit met 'kleine' blokken, maar het aantal mogelijkheden loopt snel op. (Op pyth.eu kun je weer Python code vinden om er zelf mee te spelen.) Eigenlijk is er nog steeds verrassend weinig bekend over Chomp, hoewel het al meer dan 50 jaar oud is. Sommige beginsituaties zijn echter goed te analyseren zonder computer.

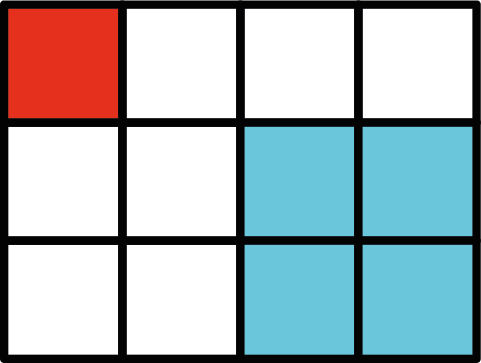
Kijk eens naar de situatie waarbij er nog maar twee stroken over zijn: één horizontale en één verticale strook van één blokje breed (zie figuur 4 hierboven). Als de stroken even lang zijn, dan is het een verloren situatie voor wie aan zet is. Dit geldt immers als alleen nog het rode blokje linksboven over is (de stroken hebben dan lengte nul). Bovendien, als de stroken niet even lang zijn, dan kan degene die aan de beurt is ze altijd even lang maken, door van de langere strook een stuk af te happen. Dit is dus net als Nim met twee hoopjes, maar dan met de regel dat degene die als laatste pakt verliest.

Een strook van breedte twee (zie figuur 5) is ook nog eenvoudig te doorgronden. Merk op dat de onderste rij nooit langer kan zijn dat de bovenste rij. Het is een verloren situatie voor de eerste speler als de rij zonder het rode blokje precies één blokje korter is dan de bovenste rij. Het losse rode blokje voldoet hier immers aan. Bovendien, als dit niet het geval is, dan kan degene die aan zet is er altijd voor zorgen dat de rijen maar één in lengte verschillen. Als ze namelijk even lang zijn, dan hap je één blokje rechts van de onderste rij. En als ze niet even lang zijn, dan hap je net genoeg van de bovenste rij om de ander met een verloren stand op te zadelen.

Een blok dat vierkant begint is dan ook makkelijk te winnen. Zie je hoe? Hint: Maak gebruik van de voorgaande kennis. En daar houdt de eenvoud zo'n beetje op. Er is een tijd geweest dan men dacht dat er maar één winnende zet is als je met een rechthoekig blok begint. Maar dat blijkt niet zo te zijn. Het kleinste tegenvoorbeeld begint met een $8\times10$ blok. Dat kun je met de Python code (te vinden via de knop [Bekijk oplossing] hieronder) mooi onderzoeken.

Zelfs blokken van de vorm $3\times N$ (zie figuur 6A t/m 6F) zijn nog niet in hun algemeenheid opgelost. Elke situatie is dan te kenmerken door drie getallen $p$, $q$, $r$ met $p \ge q \ge r \ge 1$, die de lengtes van de eerste, tweede en derde rij voorstellen (als $r = 0$ dan zijn er maar twee stroken). Men heeft dit vergaand met de computer onderzocht en er is wel wat structuur ontdekt, maar het spel is nog niet gekraakt. Wel heeft men kunnen vaststellen dat voor $N \le 130\,000$ de winnende beginzet uniek is. De tabel hieronder vertelt de afmeting van de winnende hap voor wat meer waarden van $N$. Mogelijk kunnen jullie in de zomervakantie hier nog wat over ontdekken. Al is het maar een patroon in het aantal rijen ($1$ of $2$) dat de winnende hap pakt.

$N$	hap	$N$	hap	$N$	hap	$N$	hap	$N$	hap	$N$	hap
$1$	$2\times1$	$6$	$2\times3$	$11$	$2\times5$	$16$	$2\times7$	$21$	$2\times9$	$26$	$1\times8$
$2$	$1\times1$	$7$	$1\times3$	$12$	$1\times4$	$17$	$1\times5$	$22$	$1\times7$	$27$	$2\times12$
$3$	$2\times2$	$8$	$2\times4$	$13$	$2\times6$	$18$	$2\times8$	$23$	$1\times7$	$28$	$2\times12$
$4$	$2\times2$	$9$	$1\times3$	$14$	$1\times4$	$19$	$1\times6$	$24$	$2\times11$	$29$	$1\times9$
$5$	$1\times2$	$10$	$2\times5$	$15$	$2\times7$	$20$	$2\times9$	$25$	$2\times11$	$30$	$2\times13$

 

$\color{navy}{Veel\ plezier\ met\ spelen.\\ Deze\ zomer\ krijgen\ Milli\ en\ Mu\ een\ computer\\ en\ gaan\ ze\ zelf\ wat\ programmeren.}$

 

Bekijk oplossing