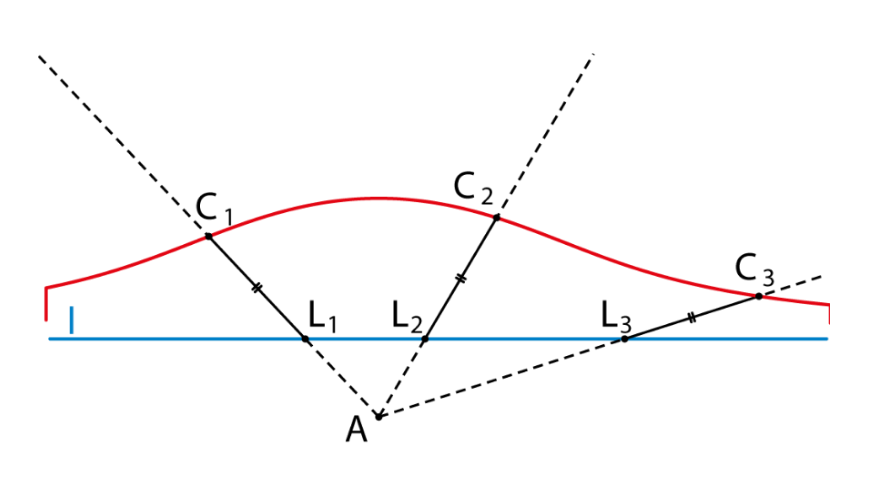
Stel, je hebt een punt $A$ en een rechte lijn $l$. Verder heb je een latje $m$ dat om punt $A$ kan draaien. Laat het latje snijden met lijn $l$: dat levert snijpunt $L$ op. Vervolgens bepaal je punt $C$ door op het latje een vaste afstand $d$ af te passen. Vervolgens draai je het latje om punt $A$ heen, zodat je verschillende punten $L$krijgt, en steeds pas je dezelfde afstand $d$ af, zodat je uiteindelijk ook een heleboel verschillende punten $C$ krijgt. Al die punten $C$ vormen samen een kromme, die conchoïde wordt genoemd. Althans, deze kromme is één tak van de conchoïde. In bovenstaande figuur zijn drie punten $C$ op de conchoïde getekend. Het punt $A$ heet de pool van de conchoïde.

Figuur 2

Figuur 3

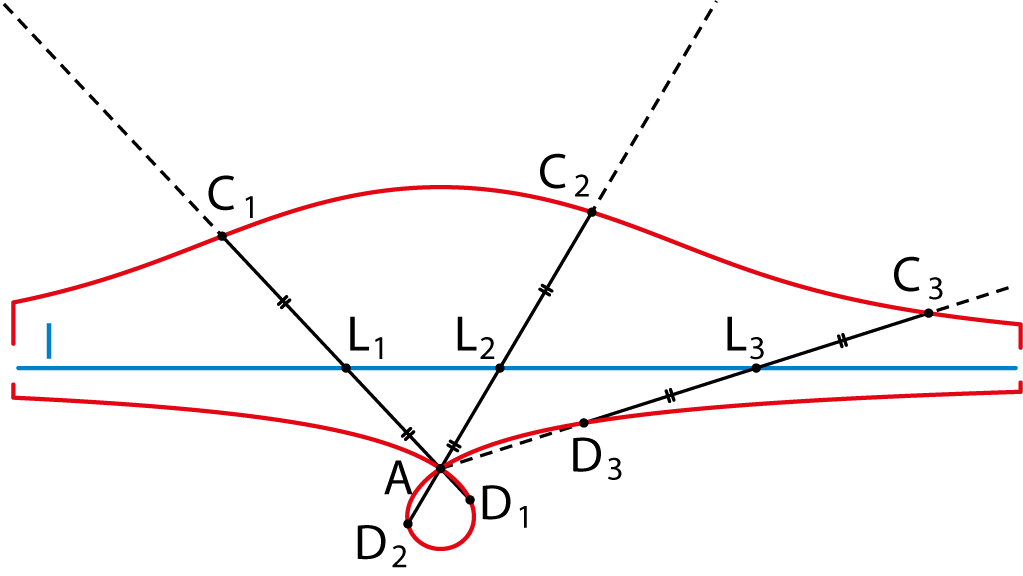
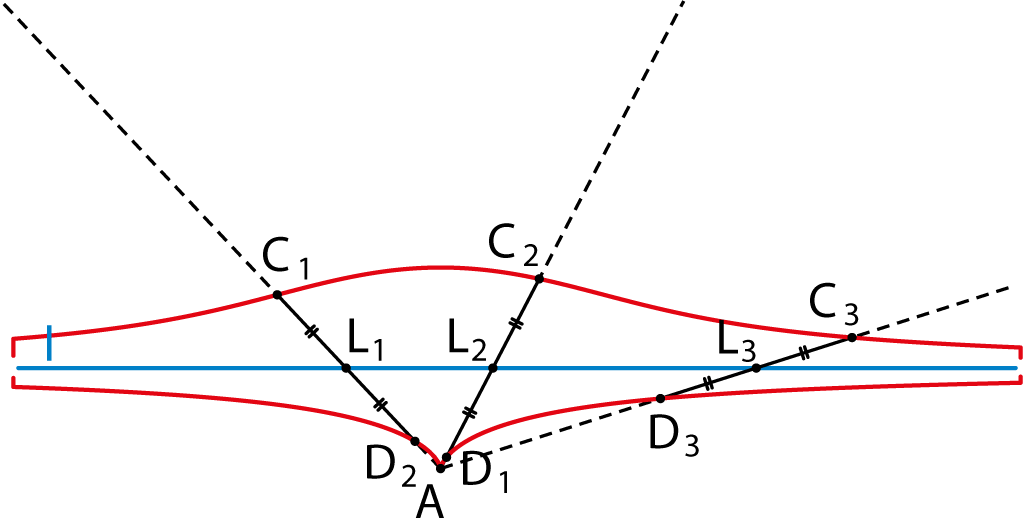
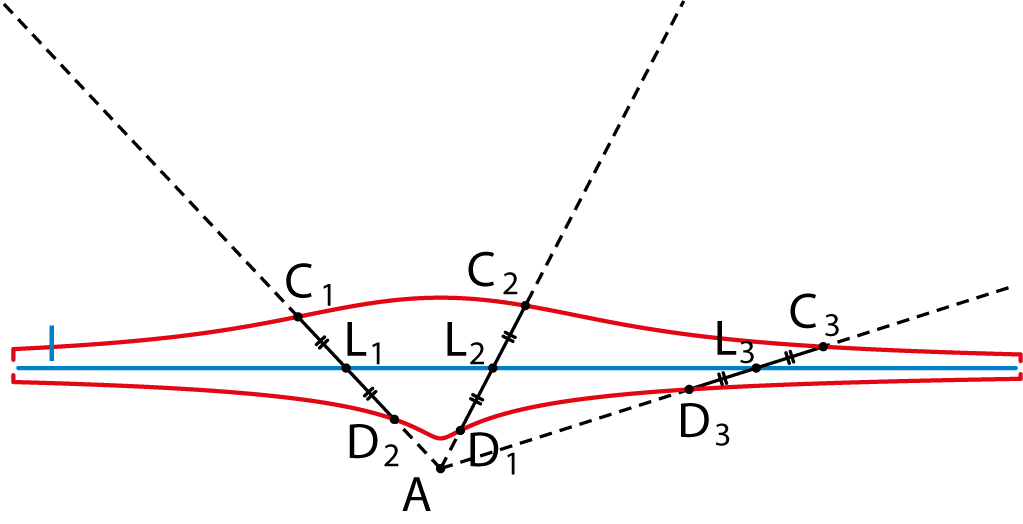
De andere tak van de conchoïde kun je tekenen door ook aan de andere kant van $L$  op dezelfde afstand een punt af te passen op lijn $AL$. Het resultaat zie je in figuur 1. In dit voorbeeld is de afstand $d=|CL|$ groter dan de afstand van $A$ tot lijn $l$, maar dat hoeft natuurlijk niet per se zo te zijn. Als die afstanden gelijk zijn, ziet de conchoïde er uit als in figuur 2. En als $d$ kleiner is dan de afstand tussen $A$ en $l$, krijg je een conchoïde als in figuur 3. In deze laatste gevallen is de ‘lus’ aan de onderkant dus verdwenen.

Geschiedenis

Aan de conchoïde is de naam van Nicomedes verbonden, een oude Griek die leefde in de derde eeuw voor Christus. Nicomedes gebruikte de kromme in zijn zoektocht naar een manier om een willekeurige hoek in drie gelijke delen te verdelen door middel van een passer-en-latje-constructie, één van de drie beroemde onmogelijke constructieproblemen uit de Griekse oudheid. De conchoïde is dan dus eigenlijk geen toegestaan hulpmiddel, maar daarmee lukt het wel.

In de zeventiende eeuw was de conchoïde ook in zwang. Descartes gebruikte hem in zijn beroemde werk La Géométrie (1637) als voorbeeldkromme om zijn methode uit te leggen. Descartes had een methode gevonden om een ‘normaal’ (loodlijn) te vinden op krommen. En als je een lijn kunt vinden die loodrecht op een kromme staat, is het vinden van de raaklijn natuurlijk eenvoudig: die staat dan weer loodrecht op de loodlijn in het punt op de kromme. Hiermee gaf Descartes een andere manier om raaklijnen te vinden dan bijvoorbeeld Fermat. Pas later werd door Newton en Leibniz onafhankelijk van elkaar de analyse uitgevonden zoals wij die nu kennen, waarbij raaklijnen bepaald worden met behulp van de afgeleide.

Driedeling van de hoek

Figuur 4

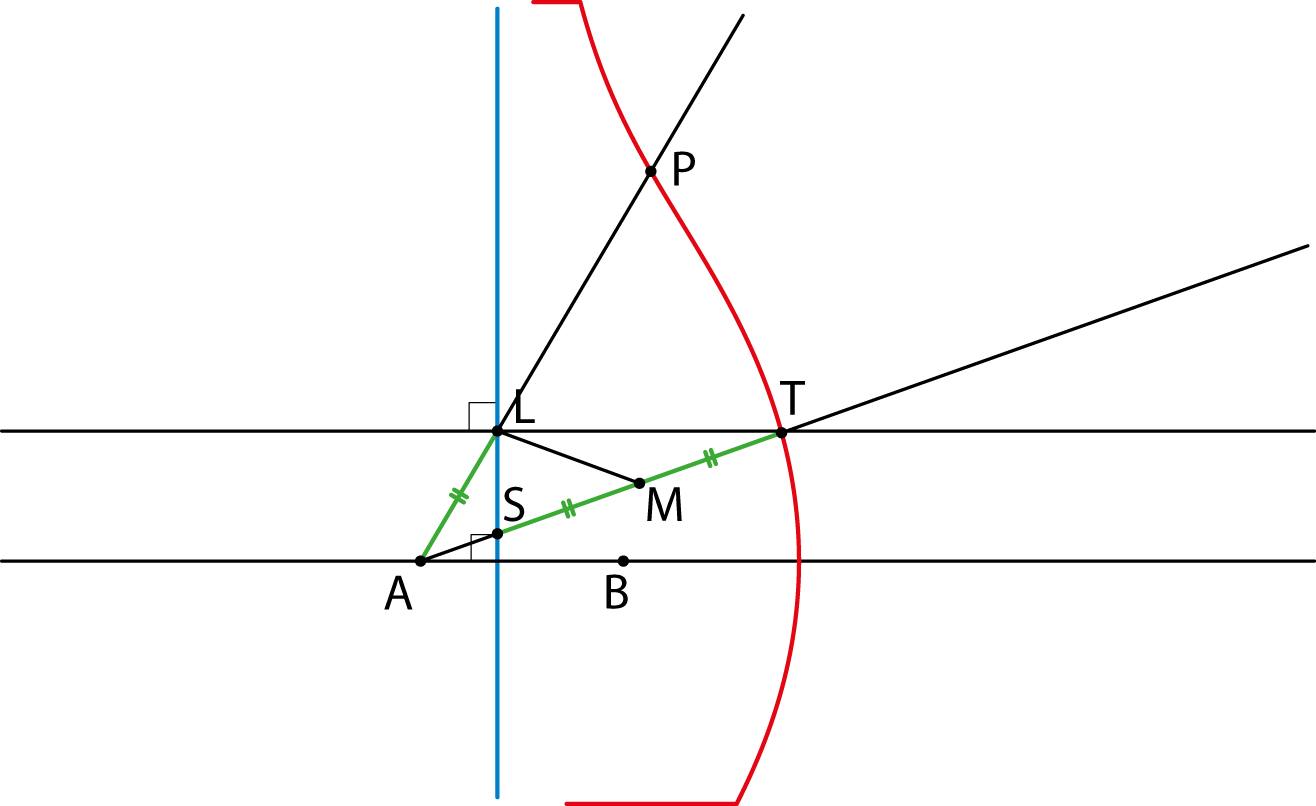
Hoe kun je de conchoïde gebruiken om een willekeurige hoek in drie gelijke delen te verdelen? We geven hier een methode, die overigens alleen voor scherpe hoeken werkt. De beschreven stappen zijn allemaal uitgevoerd in figuur 4. Noem het hoekpunt van de gegeven hoek $A$ en markeer op elk van de benen van de hoek een punt: $B$ en $L$. Teken de conchoïde met pool $A$ en neem voor lijn $l$ de loodlijn op $AB$  door $L$, waarbij de vaste afstand tussen $L$ en het bijbehorende punt $P$ op de conchoïde gelijk is aan 2$|AL|$.

Teken nu de loodlijn op lijn $l$ vanuit punt $L$. Die loodlijn snijdt de conchoïde in punt $T$. Het snijpunt van $AT$ en $l$ noemen we $S$. Omdat $T$ op de conchoïde ligt, geldt dus dat $|TS|=$2$|AL|$. Punt $M$ is het midden van $ST$.

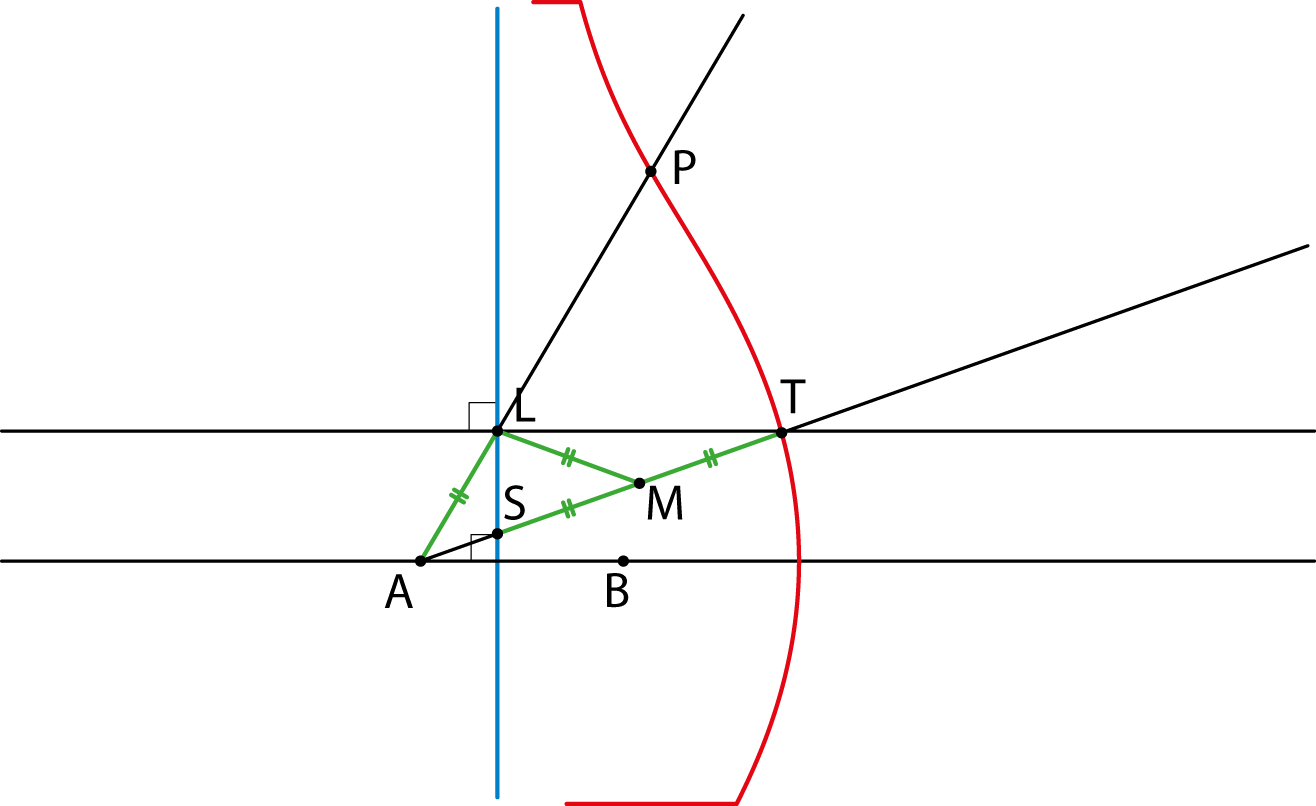
Figuur 5

De bewering is nu dat \(\angle BAT\) precies een derde is van \(\angle BAL\). Om dat te bewijzen, hebben we nog één ingrediënt nodig: de lengte van $LM$. Merk op dat \(\angle SLT\) een rechte hoek is. Uit de stelling van Thales volgt dan dat $L$ op de cirkel ligt met middellijn $LT$. Van die cirkel is $M$ uiteraard het middelpunt en de straal is dan $|MS|=|AL|$. Dan is $|ML$ dus ook gelijk aan $|AL|$ (zie figuur 5).

Nu volgt redelijk eenvoudig dat \(\angle BAS\) een derde is van \(\angle BAL\). Probeer dat eens zelf te bewijzen.

 

 

 

Bekijk oplossing