Doel

Het doel is op een horizontaal vlak de krommen te tekenen die worden gevolgd door de punt van de schaduw van een gnomon op bijzondere dagen: zonnewendes, nachteveningen, de verjaardag van een beroemd persoon, enzovoort. De aanleg van deze gnomon-datumwijzer vereist het gebruik van een complexe formule, die bijvoorbeeld in het programma Geogebra kan worden ingevoerd.

Voorbereiding

Het is raadzaam, na bestudering van onderstaande tekst, eerst een gnomon-datumwijzer op schaal te maken, zoals hieronder weergegeven.

Uitvoering

Voor de uitvoering is in de eerste plaats een zonnig horizontaal plein noodzakelijk. De afmetingen van het plein zijn afhankelijk van de uitkomst van je berekeningen, dus maak eerst een plan waar de berekeningen onderdeel van zijn.

Op het plein wordt een gnomon met hoogte $a$ perfect verticaal vastgezet. In de loop van de dag beschrijft de schaduw van de punt van de gnomon hyperbolische krommen op de grond - behalve bij de equinoxen, dan volgt de schaduw een rechte lijn.

Deze lijnen worden getekend met behulp van een assenstelsel. Teken het assenstelsel met de coördinatenlijnen bijvoorbeeld met krijt op een betegeld schoolplein.

Dit assenstelsel moet voldoen aan bepaalde eisen.

• De gnomon staat in de oorsprong van het assenstelsel.
• Is de gnomon geplaatst, dan is de volgende stap het tekenen van de meridiaan van de plaats waar de voet van de gnomon staat. Dit is een noord-zuid lijn. Zorg ervoor dat dat met grote precisie gebeurt. Daar is een eenvoudige methode voor. Zoek op internet (bijvoorbeeld www.suncalc.org) op welk tijdstip van de dag van aanleggen de zon precies in het zuiden staat. De schaduw van de gnomon wijst dan naar het noorden.
• Dan een loodrecht assenstelsel tekenen, met de voet van de gnomon als oorsprong. De $y$-as wijst naar het noorden (en ligt dus op de meridiaan van de plaats) en de $x$-as wijst naar het oosten.
• Voor een gegeven declinatie $\delta$ en breedte $\varphi$ is de formule met $x$ als variabele:
  $$y=\frac{-a\cdot \sin(\varphi)\cdot\cos(\varphi)+\sin(\delta)\cdot\sqrt{x^2\left(\cos^2(\varphi)-\sin^2(\delta)\right)+a^2\cdot\cos^2(\delta)}}{\sin^2(\delta)-\cos^2(\varphi)}.$$

Hierin is:

• $\alpha$: de hoogte van de gnomon
• $\varphi$: de breedtegraad van de gnomon
• $\delta$: de declinatie die hoort bij de kromme $=$ de breedgraad waar de zon loodrecht boven staat, op de dag die bij de kromme hoort; zommerzonnewende: $\delta = 23{,}44^{\rm o}$; winterzonnewende: $\delta = -23{,}44^{\rm o}$; equinox: $\delta = 0^{\rm o}$.

Het kan een overweging zijn om voor $a = 1$ meter te nemen. Daarmee krijgen we een iets eenvoudiger formule.

$$y=\frac{-\sin(\varphi)\cdot\cos(\varphi)+\sin(\delta)\cdot\sqrt{x^2\left(\cos^2(\varphi)-\sin^2(\delta)\right)+\cos^2(\delta)}}{\sin^2(\delta)-\cos^2(\varphi)}.$$

Gevalsonderscheiding:

1. Equinox (nachtevening: 21 maart en 23 september)
   Nemen we $\varphi = 52^{\rm o}$ en $\delta=0$ dan volgt voor 21 maart en 23 september:
   $$\begin{split}y&=\frac{-\sin(52^{\rm o})\cdot\cos(52^{\rm o})+\sin(0)\cdot\sqrt{\dots}}{\sin^2(0)-\cos^2(52^{\rm o})}\\ 
   &=\frac{-\sin(52^{\rm o})\cdot\cos(52^{\rm o})+0\cdot\sqrt{\dots}}{0-\cos^2(52^{\rm o})} \\
   &=\frac{-\sin(52^{\rm o})\cdot\cos(52^{\rm o})}{-\cos^2(52^{\rm o})} \\
   &=\frac{-\sin(52^{\rm o})}{-\cos(52^{\rm o})}=\tan(52^{\rm o})).
    \end{split}$$
   Dus: $y=\tan(52^{\rm o})$. Dat is van de vorm $y = $ constante en de grafiek is dus een lijn die evenwijdig is met de $x$-as.
2. Zomerzonnewende (zomersolstitium)
   Nemen we $\varphi = 52^{\rm o}$ en $\delta=23{,}44^{\rm o}$ dan volgt voor 21 juni:
   $$y=\frac{-\sin(52^{\rm o})\cdot\cos(52^{\rm o})+\sin(23{,}44^{\rm o})\cdot\sqrt{x^2\left(\cos^2(52^{\rm o})-\sin^2(23{,}44^{\rm o})\right)+\cos^2(23{,}44^{\rm o})}}{\sin^2(23{,}44^{\rm o})-\cos^2(52^{\rm o})}.$$
3. Winterzonnewende (wintersolstitium)
   Bij $\varphi=52^{\rm o}$ en $\delta=-23{,}44^{\rm o}$ dan volgt voor 21 december:
   $$y=\frac{-\sin(52^{\rm o})\cdot\cos(52^{\rm o})+\sin(-23{,}44^{\rm o})\cdot\sqrt{x^2\left(\cos^2(52^{\rm o})-\sin^2(-23{,}44^{\rm o})\right)+\cos^2(-23{,}44^{\rm o})}}{\sin^2(-23{,}44^{\rm o})-\cos^2(52^{\rm o})}.$$

Deze formules dienen met grote precisie te worden ingevoerd in Geogebra.

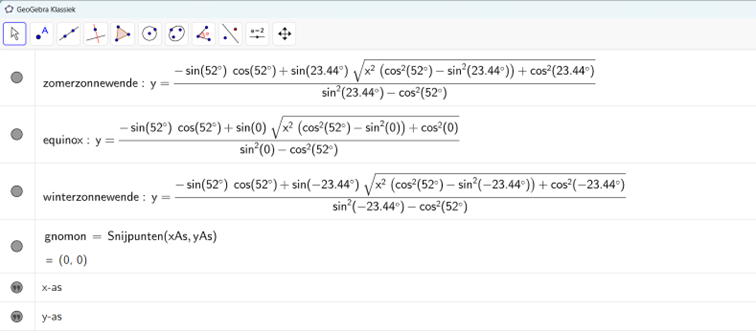
zomerzonnewende(x) = (-sin(52°) cos(52°) + sin(23.44°) sqrt(x² (cos²(52°) - sin²(23.44°)) + cos²(23.44°))) / (sin²(23.44°) - cos²(52°))
equinox: y = (-sin(52°) cos(52°) + sin(0°) sqrt(x² (cos²(52°) - sin²(0°)) + cos²(0°))) / (sin²(0°) - cos²(52°))
winterzonnewende(x) = (-sin(52°) cos(52°) + sin(-23.44°) sqrt(x² (cos²(52°) - sin²(-23.44°)) + cos²(-23.44°))) / (sin²(-23.44°) - cos²(52°))
gnomon : Snijpunten(xAs, yAs) 

Als je de formules goed hebt overgenomen krijg je de volgende grafieken:

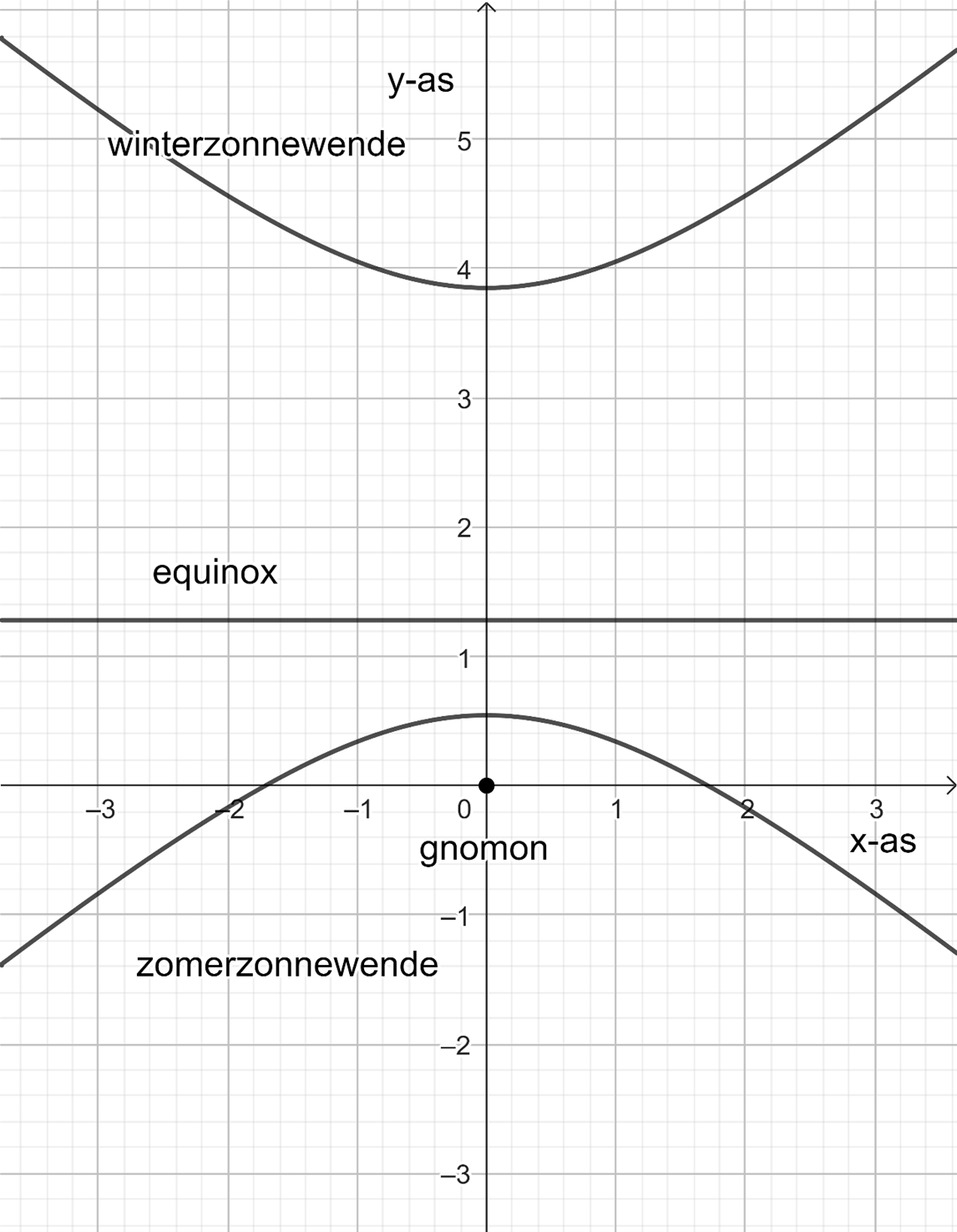
Aan deze figuur kan ook de hyperbool worden toegevoegd die hoort bij een beroemd persoon. Op bijvoorbeeld een Jacob Cats School kan de declinatie worden ingevoerd die hoort bij de geboortedatum van Jacob Cats (10 november 1577 $\Rightarrow \delta = -17,343^{\rm o}$; zie declinatietabel van de Zonnewijzerkring).

Bedenk dat in dit voorbeeld gekozen is voor breedtegraad $52^{\rm o}$, terwijl in Nederland de breedtegraad varieert van ongeveer $51^{\rm o}$ tot ongeveer $53^{\rm o}$. Waarschijnlijk moet je de breedtegraad dus aanpassen.

Is de belijning eenmaal met behulp van een assenstelsel getekend, dan kan de zonnewijzer verder worden verfraaid. Op bijvoorbeeld de Prinses Margriet school kunnen tussen de lijnen margrieten worden gesjabloneerd.

Maak er wat moois van!