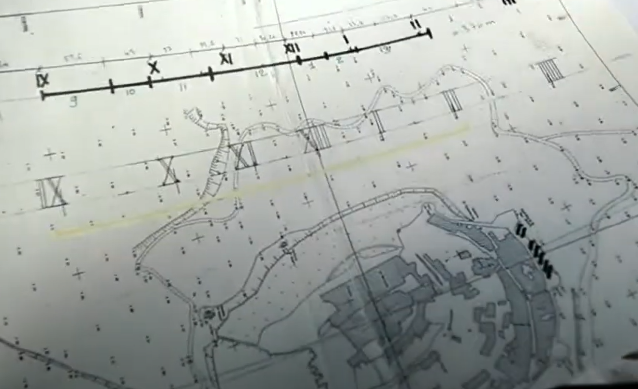
Het was in 1988 dat het eiland onder de naam Le Mont Solaire tijdelijk als zonnewijzer fungeerde. De torenspits met daarop het gouden beeld van Sint Michael deed dienst als schaduwwerper en dat geeft een idee van de afmetingen, want de heilige troont op meer dan 150 meter hoogte. Het installeren van een zonnewijzer op de Mont-Saint-Michel was het geesteskind van Fanchon en Laurent Maget. Dit, op zijn zachtst gezegd originele idee, ontstond tijdens het beklimmen van de klokkentoren van de abdij. De schaduw van de Mont was te zien op het wad (afbeelding 1). De vorm van de berg, en dus van zijn schaduw, vonden ze ideaal geschikt voor een zonnewijzersteel en bovendien vormde de lichte en homogene modder die de berg omgeeft een uitstekend projectievlak.

Om redenen die te maken hebben met zowel het weer als het aantal bezoekers van de Mont, was het in eerste instantie vanzelfsprekend om de Mont Solaire in de zomer te laten functioneren. Maar de ontwerpers werden al snel met de neus op de feiten gedrukt: de schaduw om 12:00 zonnetijd in de zomer (= 14:08 kloktijd) bereikt het strand niet.

Toen kwamen ze op het idee om de zonnewijzer niet op 21 juni (de zonnewende) maar op de lente-equinox (21 maart) of de herfstequinox (23 september) te installeren. Uiteindelijk is er vanwege het weer gekozen voor de herfst. Er was in september 44% kans op zonneschijn, vergeleken met 39% in maart. De lengte van de schaduw om 12:00 zonnetijd op 23 september 1988 is 171,87 meter.

Opgave 1 Open de site www.suncalc.org Vul als locatie in: Mont-Saint-Michel France. Zoek het eiland en schakel over op Esri Satellite modus (rechtsboven in beeld). Zoom zodanig in dat de namen van gebouwen te lezen zijn. Zet het rode oogje midden op de torenspits. Vul als datum in: 21 juni 1988. Eerst jaartal veranderen, dan op 21 juni zetten en vervolgens afsluiten met [DONE]. Bij culminatie (hoogste stand van de zon) staat: 14:08. Stel de tijd, m.b.v. de schuiver op de tijdbalk hierop in. Vul als hoogte van de schaduwwerper in: 150.  Controleer of de lengte om 12:00 op 23 september 1988 inderdaad bijna 172 is. Beweeg de schuiver op de tijdbalk en zie hoe de schaduw langer wordt naar links en naar rechts. De eindpunten van de schaduw liggen op een vloeiende curve. In dit artikel gaan we onderzoeken wat voor een curve het is. Opgave 2 Controleer met Suncalc dat rond 23 september de uurpunten redelijk op een rechte lijn liggen. Dat is ook echt zo en op het waarom daarvan wordt verderop in dit artikel ingegaan.

De uitvoering

De installatie vergde dagen van berekeningen en tests ter plaatse. Het werd al snel duidelijk dat een zeer sterke constructie moest worden gemaakt.

Vrijwilligers van het Franse leger werd ingezet om op een oost-west lijn ten noorden van het eiland honderden aluminium platen van 1 m2 zó te verankeren, dat een tijdschaal van Romeinse cijfers ontstond.

Voor deze verankering werden lange ijzeren buizen de bodem van de baai ingeslagen. Op deze buizen bevestigde men de aluminium platen. De opstelling moest kunnen standhouden tegen de altijd krachtige getijdenwerking (verschil tussen eb en vloed is 14 meter) en de soms forse golven in de baai.

De wijzerplaat mat 23 m × 1125 m. Hij bestond uit 7 Romeinse cijfers, van IX tot III en stippen bij de halve uren. Rond de herfstequinox van 1988 trok bij zonnig weer de schaduw van Saint Michel in een min of meer rechte lijn langs de Romeinse cijfers. De reflectie, samen met het schaduwspel van de wolken moet een prachtig gezicht geweest te zijn.

Met de uitvoering, die zo'n driekwart jaar duurde, hielpen bijna 80 vrijwilligers. Eind september was alles weer keurig opgeruimd en wat ons rest zijn de beschrijvingen en videofragmenten op internet.

Waarom ligt de tijdsChaal op zo'n keurige reChte?

Om deze vraag te beantwoorden biedt onderzoek uitkomst: we bekijken de beweging van de zon in de loop van een dag. We doen net of de zon beweegt over een grote bol met onbepaalde straal, de hemelbol. Een doorzichtig dopje op een Michelin atlas geeft een aardig beeld van een hemelbol, gezien vanuit Mont-Saint-Michel (afbeelding 2).

De beweging kan worden ontleed in twee bewegingen: een horizontale draaiing over een hoek die we azimut noemen en een verticale draaiing over een hoek die we zonshoogte noemen (zie afbeeldling 3).

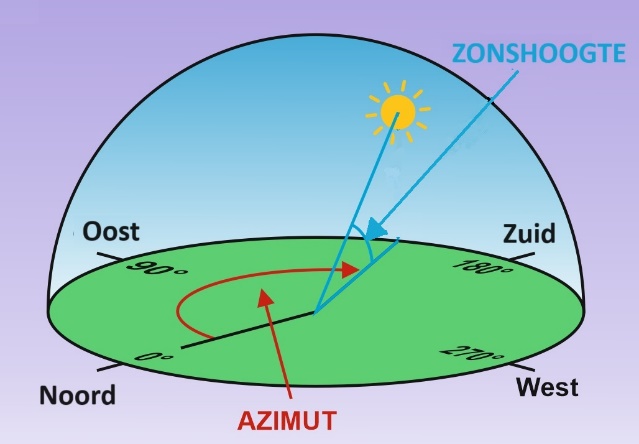
Opgave 3 Open www.suncalc.org.  Neem als datum de dag van vandaag. Verplaats het schuifje in de tijdbalk bovenin van links naar rechts. Herhaal dit enkele malen en zie hoe azimut en altitude (= zonshoogte) in de loop van een dag veranderen.

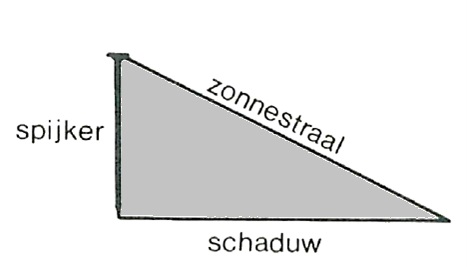
Om duidelijke tekeningen te kunnen maken, versimpelen we de Mont-Saint-Michel tot een grote spijker. (Laat ze het daar maar niet horen! ). Aan de niet-zonzijde van de spijker bevindt zich een driehoekig schaduwvlak dat met de zon meedraait en langer of korter wordt afhankelijk van de zonshoogte (afbeelding 4).

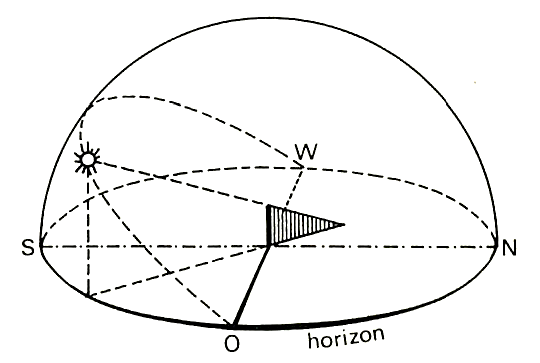
Dit combinerend met een plaatje van de hemelbol geeft afbeelding 5. 

Als je, verspreid over het jaar en met mooi weer, de beweging van de zon over de hemelbol zou volgen, zou je het volgende opvallen:

• de zon volgt elke dag een baan, die de vorm heeft van een cirkelboog (het gedeelte onder de horizon zien we niet!); alle zonnebanen zijn evenwijdig;
• de punten van opkomst en ondergang veranderen van dag tot dag;
• de hoogste stand van de zon verandert van dag tot dag. 

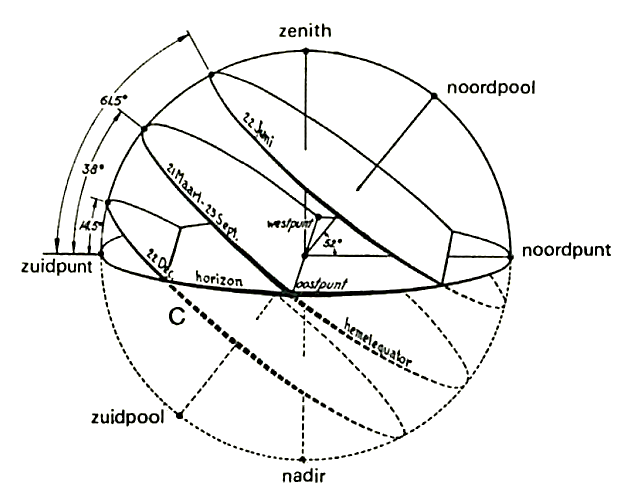
In afbeelding 6 zijn drie verschillende dagbanen van de zon over de hemelbol getekend. Als we deze afbeelding vanuit Mont-Saint-Michel bekijken, vinden we het verloop van de schaduw-eindpunten.

Uit afbeelding 6 lichten we een dagbaan $C$ en het horizontale vlak $H$. Loodrecht op dit horizontale vlak staat de spijker (met top $T$), die voor de nodige schaduwen zorgt.

$T$ blijkt de top van een kegel te zijn met $C$ als zogenaamde richtkromme (afbeelding 7). 

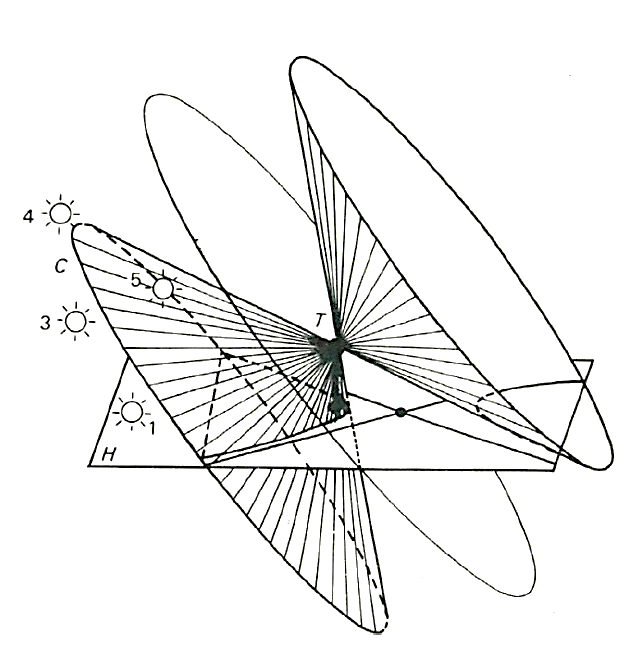
De mantel van de kegel wordt gevormd door die zonnestralen, die nog juist de spijker passeren (zie zonnestraal in afbeelding 4).

De kegel wordt gesneden door het horizontaal vlak H, dat is dus het wad bij Le Mont- Saint-Michel. De snijkromme blijkt een kegelsnede te zijn. Daarvan zijn vier hoofdtypen: (1) cirkel, (2) ellips, (3) parabool, (4) hyperbool (zie afbeelding 8).

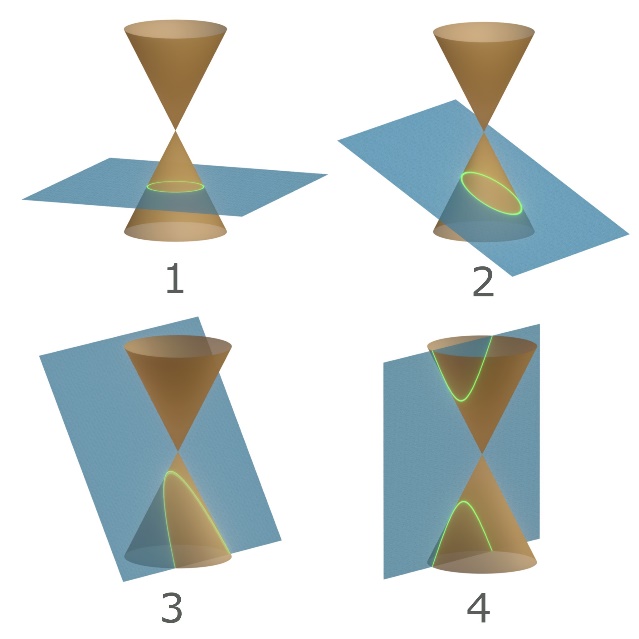
Op het wad voor de Mont-Saint-Michel vormen de eindpunten van de schaduwen zo'n snijkromme. 

Bij opkomst en ondergang van de zon zijn de zonnestralen die op het kegeloppervlak liggen, evenwijdig met het wad en veroorzaken op die momenten dus "oneindig" lange schaduwen. Dan moet er wel sprake zijn van een hyperbool. Dat is bijna het hele jaar zo. Maar er is (theoretisch gesproken) tweemaal per jaar een uitzondering. Dat is het geval wanneer de dagbaan van de zon samenvalt met de hemelequator (de middelste cirkel in afbeelding 7). Deze equinox doet zich steeds opnieuw voor op 21 maart en 23 september. Het topje van Saint-Michel ligt dan namelijk in het vlak van de 'zonnebaan'. Er is dan geen sprake meer van een kegel, maar van een cirkel waarvan de muts van Saint Michel het middelpunt is. De schaduweindpunten liggen dan min of meer evenwijdig met de middellijn van die cirkel (afbeelding 7). Daarmee is de vraag beantwoord. 

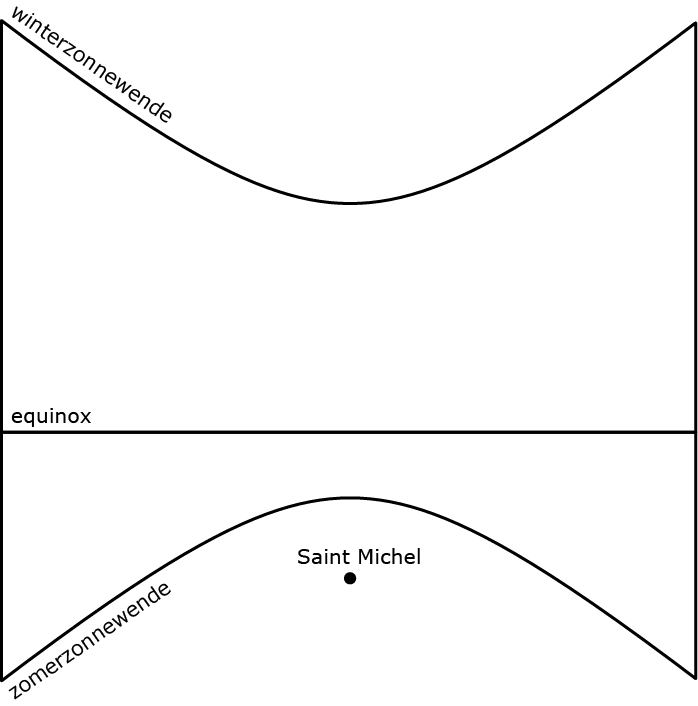
De grafiek in afbeelding 9 geeft de curves weer die op vier speciale dagen in het jaar door de eindpunten van de schaduwen zouden kunnen worden getrokken als Le Mont Solaire de hele dag beschenen wordt door de zon.

Opgave 4 Welke data horen bij equinox? Op welke plaatsen op aarde vormen de schaduw-eindpunten een cirkel? Denk aan afbeelding 8. Zelfde vraag voor ellips. Zelfde vraag voor parabool.

Zelf aan de slag

Via de knop [Bekijk oplossing] hieronder kun je een uitgebreide instructie vinden om zelf een gnomon (zoals op afbeelding 10) op het schoolplein te plaatsen en bijbehorende datumlijnen te tekenen; de plattegrond ziet er uit als in afbeelding 11, waarin een bescheiden suggestie om de helften lente-zomer en herfst-winter verschillend in te kleuren . Alle datumlijnen liggen tussen de twee van de zonnewendes dus die twee zou ik zeker meenemen en die van de equinoxen ook. En je verjaardag, en die van andere belangrijke personen.

 

De tekst is mede gebaseerd op een artikel van Leen Streefland in Pythagoras 18-5.  Filmpjes van de constructie van Le Mont Solaire zijn te vinden op youtube

 

Bekijk oplossing