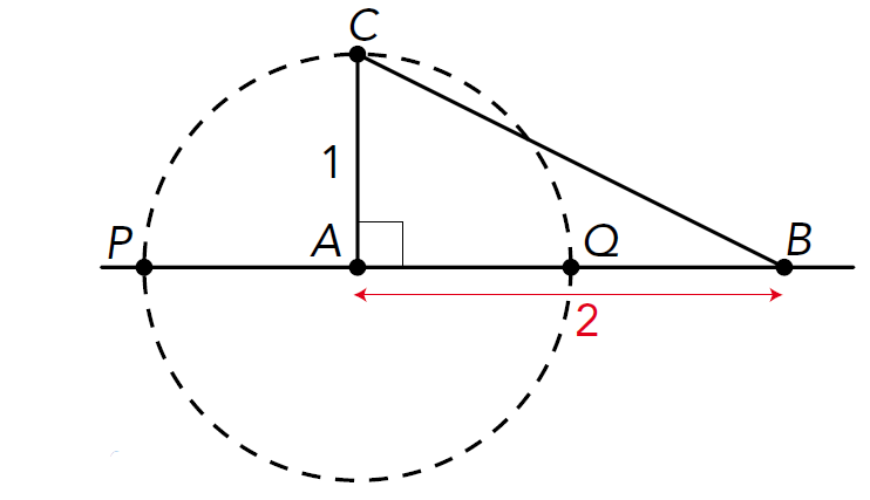
Over de gulden snede wordt vaak een heleboel onzin verteld, bijvoorbeeld dat die verhouding in allerlei oude architectuur of kunst te vinden zou zijn, en dat mensen rechthoeken met zijden in die verhouding het allermooist zouden vinden. Maar het is wel een bijzondere verhouding in wiskundig opzicht: een lijnstuk is in twee delen verdeeld volgens de gulden snede als het kleinste deel tot het grootste deel dezelfde verhouding heeft als het grootste deel tot het hele lijnstuk (zie figuur 1).

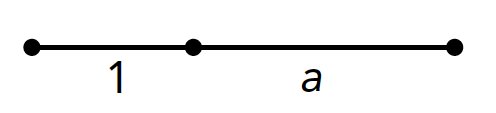
We kunnen het kleinste deel zonder verlies van algemeenheid 1 noemen (we hebben het tenslotte niet over precieze lengtes, maar over verhoudingen). Dan zegt de definitie hierboven: wanneer $a$ en 1 de gulden-snede-verhouding hebben, dan geldt 1 : $a = a$ : $(a +$ 1).

Opgave 1: Gebruik de gelijkheid 1$/a=a/(a+$1) en leid daaruit af dat $a=\frac{1}{2}+\frac{1}{2}\sqrt{5}$. (Dit getal wordt vaak $\varphi$ genoemd, de Griekse letter phi).

Opgave 2: Laat zien dat wanneer we aannemen dat juist het grootste deel van het lijnstuk 1 is, en het kleinste deel b noemen, het volgende geldt: $b=-\frac{1}{2}+\frac{1}{2}\sqrt{5}$.

De vraag naar de constructie kunnen we nu stellen als: stel dat een lijnstukje van lengte 1 gegeven is, construeer dan met passer en latje een lijnstuk van lengte $\frac{1}{2}+\frac{1}{2}\sqrt{5}$.

Opgave 3: In het artikel ‘Wortels construeren’ (Pythagoras 55-4, februari 2016, pagina 5-6) heb je geleerd om wortels te construeren. Gebruik die constructie om $\sqrt{5}$ te maken en maak daarmee vervolgens $\frac{1}{2}+\frac{1}{2}\sqrt{5}$.

Dit is één manier om de gulden-snede-verhouding te construeren. Maar dat is niet de enige. De simpelste constructie komt neer op de vraag: gegeven een lijnstuk van lengte 2, kunnen we dat lijnstuk verdelen volgens de gulden-snede-verhouding? Die vraag is dus net een beetje anders: we gaan nu niet een lijnstukje van lengte $\frac{1}{2}+\frac{1}{2}\sqrt{5}$ construeren, we gaan een lijnstuk van lengte 2 verdelen in twee stukken met verhouding (maar niet lengtes!) 1 $: (\frac{1}{2}+\frac{1}{2}\sqrt{5}$).

Die constructie gaat als volgt (zie figuur 2). Je begint met een lijnstuk $AB$ van lengte 2. Deel dat doormidden (met een middelloodlijn) en construeer vervolgens door $A$ een loodlijn op $AB$ met lengte 1. (Dat kan bijvoorbeeld door een cirkel met middelpunt $A$ en straal 1 te tekenen, en dan op de twee snijpunten $P$ en $Q$ die die cirkel heeft met lijnstuk $AB$ een middelloodlijn te construeren.) Het uiteinde van dat loodlijntje noemen we $C$.

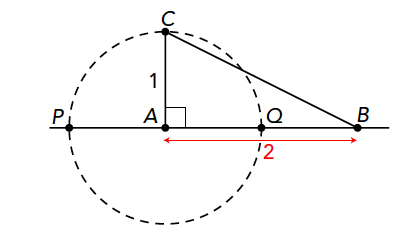
Opgave 4: Voer deze constructie zelf uit met passer en latje, dus zonder te meten. Begin dus met een willekeurig lijnstuk $AB$ en noem de lengte van dat lijnstuk 2.

Opgave 5: Hoe lang is $BC$ dan?

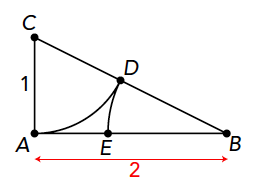
De constructie gaat als volgt verder (zie figuur 3). Teken een cirkelboogje met midden $C$ en straal $CA$. Het snijpunt met $BC$ heet $D$. Teken nu een cirkelboogje met midden $B$ en straal $BD$. Het snijpunt met $AB$ heet $E$. De bewering is nu: $E$ verdeelt het lijnstuk $AB$ volgens de gulden-snede-verhouding. In de volgende opgave ga je uitzoeken waarom dat klopt.

Opgave 6: Hoe lang is $BD$? Hoe lang is $AE$ dus? Toon aan dat $AE : EB = 1 : (\frac{1}{2}+\frac{1}{2}\sqrt{5})$.

 

Bekijk oplossing