Opgave 1. Kruislings vermenigvuldigen geeft $a^2 = a + 1$, dus $a^2 – a – 1 = 0$ en de $abc$-formule geeft ons dan twee oplossingen, waarvan $a = \frac{1}{2} + \frac{1}{2}\sqrt{5}$ de enige positieve is.

Opgave 2. Dit kan op twee manieren. Analoog aan opgave 1 vinden we $b/1 = 1/(b + 1)$, wat leidt tot $b^2 + b = 1$. De positieve oplossing van deze vergelijking is $b = – \frac{1}{2} + \frac{1}{2}\sqrt{5}$.

De andere methode gaat als volgt: blijkbaar is de verhouding $1 : a$ gelijk aan $b : 1$, ofwel $ab = 1$, en $1/( \frac{1}{2} + \frac{1}{2}\sqrt{5})$ blijkt na wat rekenwerk (zie voor een idee de oplossing van opgave 6 hieronder) inderdaad gelijk te zijn aan $-\frac{1}{2} + \frac{1}{2}\sqrt{5}$.

Opgave 3. 

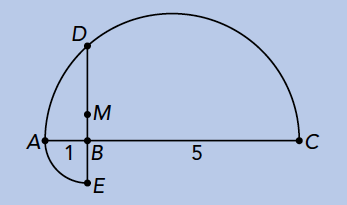
Voer de constructie uit het vorige nummer uit met lijnstukken van lengte 1 en lengte 5. Dat kwam neer op: verleng een lijnstuk van lengte 1 en pas met de passer daarop nog 5 af, dan krijgen we $AB$ van lengte 1 en $BC$ van lengte 5. Bepaal het midden van $AC$ (bijvoorbeeld door de middelloodlijn te tekenen) en teken met dat midden als middelpunt een cirkel die door $A$ en $C$ gaat. Teken vanuit $B$ een loodlijn omhoog tot hij de cirkel snijdt in $D$, dan heeft $BD$ lengte $\sqrt{5}$. Door $DB$ aan de kant van $B$ met 1 te verlengen (dat kan eenvoudig door een cirkelboogje met straal $AB$ om $B$ te tekenen) krijgen we dus een lijnstuk van lengte 1 + $\sqrt{5}$. Dit lijnstuk doormidden delen (bijvoorbeeld weer met een middelloodlijn) levert het middelpunt $M$ op, zodat $DM = \frac{1}{2} + \frac{1}{2}\sqrt{5}$.

Opgave 4 (de constructie).

Opgave 5. De stelling van Pythagoras zegt nu dat $BC = \sqrt{1^2 +2^2} = \sqrt{5}$.

Opgave 6. Omdat $CD = 1$, geldt $BD = \sqrt{5} – 1$. Dus ook $BE = \sqrt{5} – 1$. Dus $AE = 2 – (\sqrt{5} – 1) = 3 – \sqrt{5}$. Nu moeten we dus aantonen dat $(\sqrt{5} – 1) : (3 – \sqrt{5}) = (\frac{1}{2} + \frac{1}{2}\sqrt{5}) : 1$. Dat gaat bijvoorbeeld door de deling uit te voeren en op een slimme manier met 1 te vermenigvuldigen om de wortels weg te werken uit de noemer:

\(\begin{align*} \frac{\sqrt{5}-1}{3-\sqrt{5}} &= \frac{\sqrt{5}-1}{3-\sqrt{5}} \cdot \frac{3+\sqrt{5}}{3+\sqrt{5}}\\ &= \frac{3\sqrt{5}+5-3-\sqrt{5}}{9+3\sqrt{5}-3\sqrt{5}-5}\\ &= \frac{2\sqrt{5}+2}{4} = \frac{1}{2} + \frac{1}{2}\sqrt{5}. \end{align*}\)