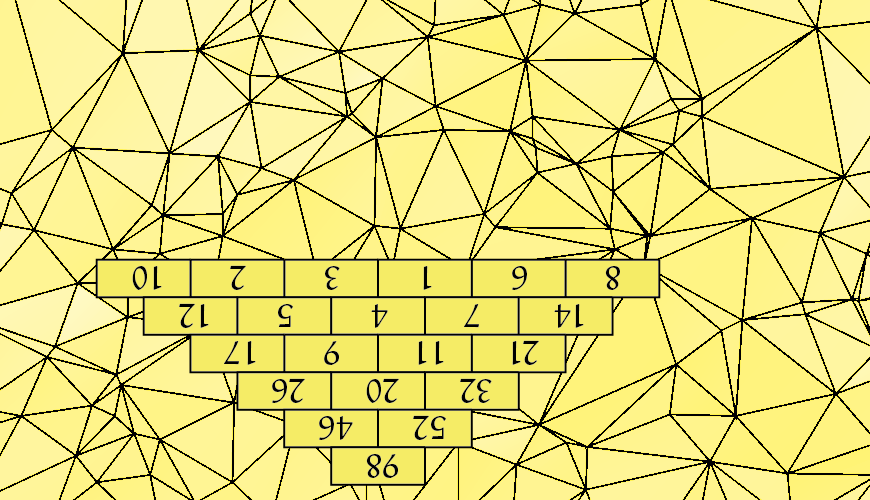
De omgekeerde driehoek van Pascal
In jaargang 57 van Pythagoras stond op de achterkant van elk nummer een variant van de driehoek van Pascal. Als je bovenin begint met vullen is de driehoek heel eenvoudig te construeren. Als je onderaan begint, is dat vullen helemaal niet zo simpel. Gelukkig hebben we Python om ons daarbij te helpen.
We gaan uit van $n$ verschillende positieve getallen (niet per se de getallen $1$ t/m $n$ en niet per se gesorteerd). We construeren een piramide, als volgt: plaats midden boven de $n$ getallen steeds de som van de twee getallen eronder. Dat levert een rij van $n - 1$ getallen op. Dan volgen $n - 2$ getallen. Uiteindelijk is er één getal bovenaan de piramide. In dit artikel zijn we alleen geïnteresseerd in piramides waarin de getallen allemaal verschillend zijn.
In figuur 1 staat een aantal piramides met verschillende getallen.
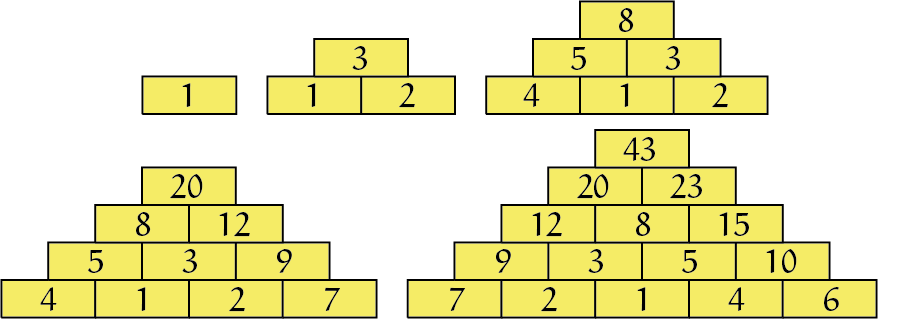
Het wiskundige aspect
We bouwen nu dezelfde piramides op met variabelen $a$, $b$, $c$, $d$ en $e$. Zie figuur 2. De uitdaging is om voor elke $n$ een piramide te vinden zodat in de top een zo’n klein mogelijk getal staat.
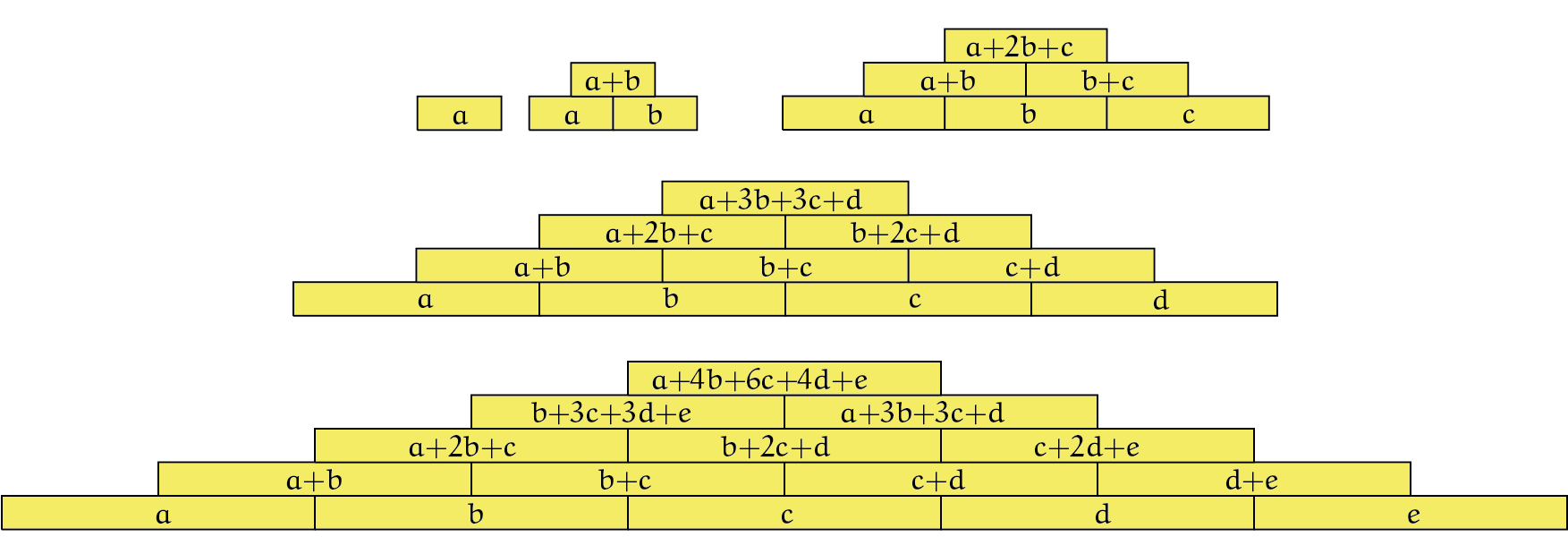
We werken enkele pogingen uit. De opdracht aan de lezer is om zelf ook iets te proberen.
Poging 1: alle permutaties uitproberen
We maken gebruik van itertools. Dit pakket bevat onder meer combinations. Met de procedure permutations(M, n) worden alle combinaties geselecteerd van lengte $n$ uit de verzameling $M$, waarbij ook de verschillende volgordes worden meegenomen. In ons geval is $M = \{1, 2, 3, …, m\}$. Hierbij is $m$ het grootste getal dat op de onderste regel staat. De keuze van $m$ is arbitrair. In de praktijk blijkt voor kleine waarden van $n$ een waarde van $m = 2n$ goed te werken. In principe volstaat het om de oplossing te laten zien met de laagste waarde aan de top, maar we laten ook een aantal andere oplossingen zien, die beter of gelijk zijn aan alle voorafgaande oplossingen.
Poging 2: Vooraf snelle berekening maken
Als je kijkt naar de diagrammen in figuur 2 dan zie je dat getallen op de onderste rij die meer naar het midden staan in een hoger veelvoud in de top terugkeren, dan getallen aan de rand. Je kunt vrij eenvoudig de topwaarde berekenen op grond van de waarden in de onderste rij, zonder de tussenliggende rijen daadwerkelijk te berekenen.
Poging 3: Dalend en dan stijgend
We zien in figuur 3 dat bij lengte 6 de optimale bodemrij $\{8, 6, 1, 3, 2, 10\}$ is. In het midden staan de kleinere getallen met daaromheen de grotere getallen. Gezien vanuit het midden is $1, 6, 8$ een stijgende rij, maar $3, 2, 10$ niet, maar wel bijna.
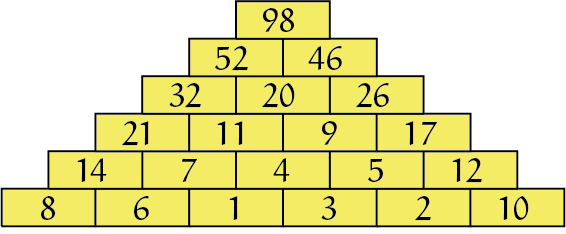
Het loont dus om vooraf te checken of de kleinere getallen in het midden staan.
Resultaten
Poging 2 levert geen verbetering op vergeleken met Poging 1 op, maar Poging 3 wel. Uiteindelijk vinden we de minimale rij topwaarden $\{8, 20, 43, 98, 212, 465\}$. Zoeken we vervolgens op internet naar deze rij, dan vinden we op de On-Line
Encyclopedia of Integer Sequences http://oeis.org/A028307 deze rij terug!
De bijbehorende code vind je onder de knop [Bekijk oplossing]
Bekijk oplossing
