Iedereen kent wel de stapeltoren van kubussen als speelgoed voor peuters. Doorgaans zijn het setjes van tien kubussen van verschillend formaat, om van groot naar klein op elkaar te leggen. Stel je nu eens een toren van kubussen voor met ribben met afnemende lengten $1, \frac{1}{\sqrt{2}},\frac{1}{\sqrt{3}},\frac{1}{\sqrt{4}},\frac{1}{\sqrt{5}},\dots,\frac{1}{\sqrt{n}},\dots$, die zonder einde de hoogte in reikt.

De oppervlakte

Hoe tellen de oppervlakten van deze kubussen op? De oppervlakte van een enkele kubus met zijn zes vierkante zijvlakken met zijden van lengte $\frac{1}{\sqrt{n}}$ is $6\left(\frac{1}{\sqrt{n}}\right)^2=\frac{6}{n}$ (de kubussen van stapeltorens zijn aan één kant open zodat ze in elkaar kunnen worden geschoven, maar hier gaat het over holle kubussen met dichte zijvlakken). Voor de totale oppervlakte van de toren volgt dan de oneindige som $6H$ met $H=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\dots+\frac{1}{n}+\dots$.

$H$ heet de harmonische oneindige som. De termen ervan zijn allemaal groter dan nul. Worden ze één voor één bij elkaar opgeteld, dan worden de sommen van het toenemend aantal termen dus steeds groter. De termen op zich worden van links naar rechts wel steeds kleiner. Er zijn dan twee mogelijkheden: (1) de stijgende sommen blijven kleiner dan een of ander getal (dat groot genoeg is) en de oneindige som heeft een eindige waarde, of (2) ze overstijgen uiteindelijk elk getal dat je maar kunt bedenken (hoe groot dat ook is) en de oneindige som is 'oneindig groot'.

Figuur 1 geeft een aanschouwelijk bewijs dat de oneindige som $H$ geen eindige waarde heeft.

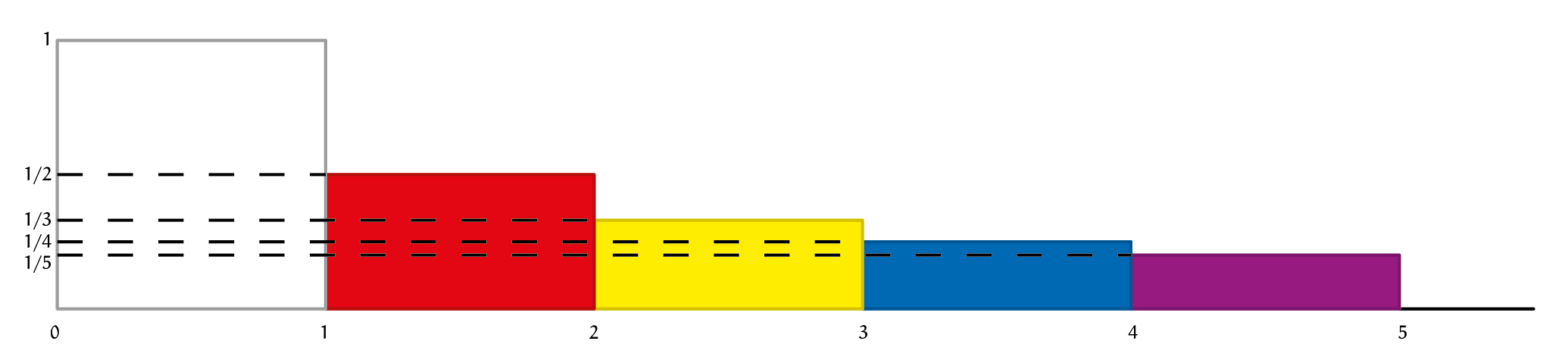
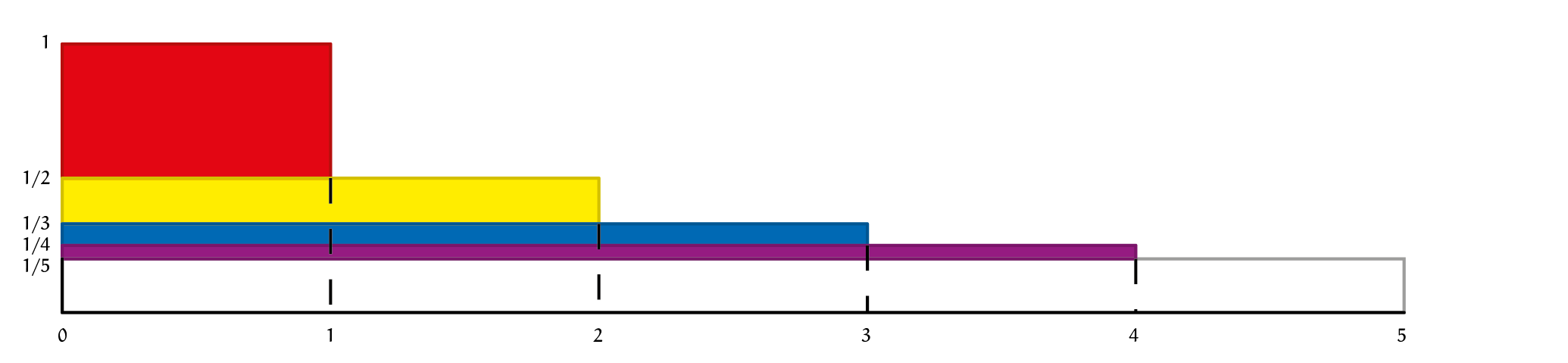
Opgave 1 Probeer voordat je verder leest uit figuur 1 te beredeneren dat $H$ geen eindige waarde heeft. (Tip: Reken na dat rechthoeken met dezelfde kleur dezelfde oppervlakte hebben.)

Figuur 1a is een weergave van de oneindige som $H$. De $n^{de}$ term van $H$ wordt voorgesteld door de oppervlakte van een rechthoek met hoogte $\tfrac{1}{n}$ en breedte $1$.

Figuur 1b heeft dezelfde totaaloppervlakte als figuur 1a. Een rechthoek in figuur 1b heeft dezelfde oppervlakte als de rechthoek in figuur 1a van dezelfde kleur, omdat ze als volgt met elkaar in verband staan. De rode rechthoek is naar links en omhoog geschoven. De gele met dikte $\tfrac{1}{3}$ is verdeeld in twee plakken van dikte $\tfrac{1}{6}$ (en dat is $\tfrac{1}{2} - \tfrac{1}{3}$), die naast elkaar zijn gelegd, de linker onder de rode rechthoek. De blauwe met dikte $\tfrac{1}{4}$ is verdeeld in drie plakken van dikte $\tfrac{1}{12}$ (en dat is $\tfrac{1}{3} - \tfrac{1}{4}$), die weer daaronder naast elkaar zijn gelegd. In het algemeen gaat de $(n+1)^{de}$ rechthoek over in $n$ plakken van dikte $\tfrac{1}{n(n+1)}$, naast elkaar gelegd op hoogte $\tfrac{1}{n+1}$ boven het interval $[0, n]$. Dit patroon zet zich onbeperkt voort. Maar dan blijft de witte rechthoek in figuur 1a met oppervlakte $1$ over!

Wordt de gezamenlijke oppervlakte van de gekleurde rechthoeken aangeduid met $X$, dan zegt figuur 1a dat $H = 1 + X$ en figuur 1b dat $H = X$. Dit kan niet als $H$ een eindige waarde heeft, dus is de som oneindig groot. Terwijl de kubussen van de toren van beneden naar boven gaand steeds kleiner worden, neemt de gezamenlijke oppervlakte van het toenemend aantal kubussen dus onbegrensd toe.

De inhoud

Hoe zit het met de inhoud? Een enkele kubus met ribbe van lengte $\frac{1}{\sqrt{n}}$ heeft inhoud $\left(\frac{1}{\sqrt{n}}\right)^3 = \frac{1}{n\sqrt{n}}$. Voor de totale inhoud van de toren volgt dan de oneindige som

$$S=\frac{1}{2\sqrt{2}}+\frac{1}{3\sqrt{3}}+\frac{1}{4\sqrt{4}}+\frac{1}{5\sqrt{5}}+\dots+\frac{1}{n\sqrt{n}}+\dots\ .$$

Voor $S$ zijn alle sommen van eindig veel termen, anders dan bij $H$, kleiner dan een vast getal. Dit volgt uit een beschouwing van de som $S_{2n+1}$ van de eerste $2n + 1$ termen. Gegroepeerd in deelsommen:

$$S_{2n+1}=1+\left(\frac{1}{2\sqrt{2}}+\frac{1}{4\sqrt{4}}+\dots+\frac{1}{2n\sqrt{2n}}\right)+\left(\frac{1}{3\sqrt{3}}+\frac{1}{5\sqrt{5}}+\dots+\frac{1}{(2n+1)\sqrt{2n+1}}\right).$$

De laatste deelsom is kleiner dan die ervoor omdat de noemers in de overeenkomende termen telkens groter zijn. Vervolgens merken we op dat $\frac{1}{4\sqrt{4}}=\frac{1}{2\sqrt{2}}\cdot\frac{1}{2\sqrt{2}}$, $\frac{1}{6\sqrt{6}}=\frac{1}{2\sqrt{2}}\cdot\frac{1}{3\sqrt{3}}$, $\cdots$, $\frac{1}{2n\sqrt{2n}}=\frac{1}{2\sqrt{2}}\cdot\frac{1}{n\sqrt{n}}$, zodat er ook nog een factor buiten haakjes kan worden gebracht:

$$S_{2n+1} < 1 + 2\left(\frac{1}{2\sqrt{2}} + \frac{1}{4\sqrt{4}} + \dots + \frac{1}{2n\sqrt{2n}}  \right) = 1 + \frac{2}{2\sqrt{2}}\left(1+\frac{1}{2\sqrt{2}} + \dots + \frac{1}{n\sqrt{n}} \right) = 1 + \frac{1}{\sqrt{2}}S_n\ .$$

Daarbij is $S_n$ de som van de eerste $n$ termen. Omdat $S_{2n+1}$ meer termen heeft dan $S_n$ en alle termen positief zijn, geldt $S_n < S_{n+1}$. Uit de twee ongelijkheden volgt $S_{2n+1}<1+\frac{S_{2n+1}}{\sqrt{2}}$, ofwel $S_{2n+1}<2+\sqrt{2}$.

Het getal $2+\sqrt{2}$ is een afschatting van de som van de eerste $2n + 1$ termen van $S$ die niet van $n$ afhangt. Elke som van een eindig aantal termen kan worden afgeschat door een $S_{2n+1}$ voor een geschikt gekozen $n$, en dus door $2+\sqrt{2}$. Dit getal is een bovengrens van de sommen van eindig veel termen. We schrijven 'een' bovengrens, want alle grotere getallen zijn vanzelfsprekend ook bovengrenzen. De kleinste bovengrens, per definitie de waarde van $S$, blijkt ongeveer $2{,}612$ te zijn.

De inhoud van de kubussen van beneden naar boven bij elkaar optellend, geeft uitkomsten die steeds dichter bij deze waarde komen.

Opgave 2 Beschouw meer algemeen de oneindige sommen $1+\frac{1}{2^p}+\frac{1}{3^p}+\dots+\frac{1}{n^p}+\dots$. $H$ en $S$ vallen hieronder voor respectievelijk $p = 1$ en $p = 3/2$ (immers $n\sqrt{n}=n^{\tfrac{3}{2}}$). Wat kun je zeggen over de termen $\frac{1}{n^p}$ voor toenemende $n$ wanneer $p < 1$, en wat betekent dat voor de oneindige som? Leid op dezelfde manier als hierboven af dat voor ieder getal $p > 1$ (gebruik dat $1 - 2^{1-p} > 0$), de hyperharmonische oneindige sommen, geldt dat $$1+\frac{1}{2^p}+\frac{1}{3^p}+\dots+\frac{1}{n^p}+\dots<\frac{1}{1-2^{1-p}}\ .$$ Waarom werkt deze afleiding niet voor $p = 1$?

De oneindige stapeltoren is dus een object met een eindige inhoud en een oneindige oppervlakte. De op het eerste gezicht moeilijk te geloven uitspraak over de pot verf in de inleiding van dit artikel staat bekend als de schildersparadox. Misschien vind je de beschouwingen hierboven niet helemaal volstaan om de paradox te aanvaarden. Bedenk dan het volgende. Als je de steeds kleinere kubussen achtereenvolgens volgiet met verf, dan beschilder je als het ware hun binnenkant. Je bedekt die zodoende met een steeds dunner laagje, omdat tegenoverliggende zijvlakken steeds dichter bij elkaar komen te liggen. Als je hun buitenkant normaal, met een laag verf van vaste dikte, beschildert, dan kost het vanaf een zekere kubus meer verf ze te bedekken dan ze te vullen. Voor het netjes afwerken van de buitenkanten is die ene pot verf niet toereikend.

Verder lezen? De harmonische en hyperharmonische oneindige sommen worden behandeld in het artikel Rare reeksen in Pythagoras 20-4. De stapeltoren wordt besproken op het YouTube-kanaal Up and Atom in de video The Painter's Paradox – These Weird Objects Will Blow Your Mind.