Als je op een grafische rekenmachine of in een algebrapakket op je computer een plot maakt van de functie $f(x) = \sin(1/x)$, met $–1 ≤ x < 0$, dan zie je een heen en weer slingerende kromme waarbij de trillingen steeds sneller na elkaar plaatsvinden. Als je aan deze grafiek het verticale lijnstuk ($V$) van (0, –1) tot (0, 1) toevoegt, dan noemt men het resultaat ($S$) de $\sin(1/x)$-kromme. In figuur 1 is $V$ rood getekend en er is wat ruimte tussen $V$ en de grafiek zichtbaar, net als in het logo van het Poolse Centrum voor Wiskunde en Informatica.

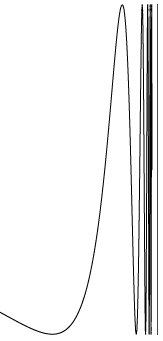
Dat heeft een praktische reden: $\sin(1/x)$ maakt oneindig veel slingeringen naar $V$ toe en die kunnen we niet allemaal plotten. Je moet die slingeringen er dus even bij denken.

Niet continu doorloopbaar

Waarom noemen we dit een kromme? Dat doen we omdat deze verzameling aan alle eisen voldoet die in de formele definitie van ‘kromme’ zijn opgenomen. (Zie ook het artikel ‘Wat is een kromme?’ in Pythagoras 46-5, april 2007; zie http://www.pyth.eu.) De verzameling is begrensd en gesloten. Dat laatste betekent dat als een punt niet tot de verzameling behoort, het meteen een positieve afstand tot die verzameling heeft. Dat kun je, met wat puzzelen, voor onze verzameling vaststellen. Vervolgens moet de verzameling samenhangend zijn, dat wil zeggen: niet te schrijven als $F ∪ G$ met $F$ en $G$ beide niet-leeg en gesloten, en met $F ∩ G = \emptyset$. Dat volgt uit een feit dat voor de hand lijkt te liggen, namelijk dat elk interval $[a, b]$ samenhangend is, maar dat toch wat werk vergt om te bewijzen. Met behulp daarvan volgt dat de grafiek van $\sin(1/x)$ samenhangend is, en daaruit volgt dat die helemaal binnen één van de verzamelingen $F$ of $G$ ligt, zeg binnen $F$. Maar dan heeft elk punt op $V$ afstand nul tot $F$ en moet dus ook tot $F$ behoren; en dan volgt $F = S$ en $G = \emptyset$. Een verzameling die gesloten, begrensd en samenhangend is wordt een continuüm genoemd. De laatste eis in de definitie van kromme is dat elk punt willekeurig kleine omgevingen heeft waarvan de rand, binnen de verzameling, geen continuüm met meer dan één punt bevat (zie figuur 2).

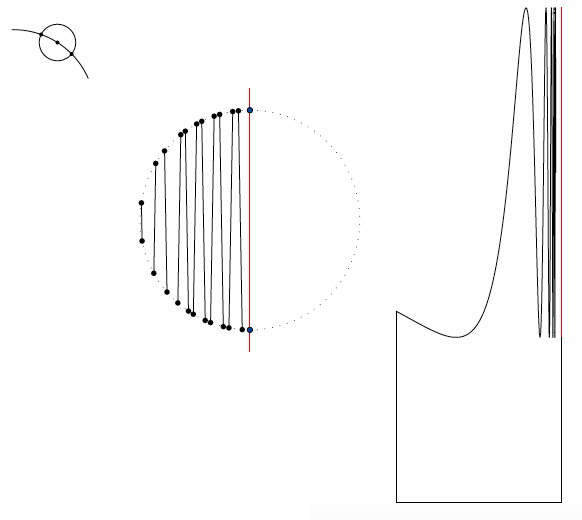
Voor een punt op de grafiek van $\sin(1/x)$ kun je kleine schijfjes nemen waarvan de rand slechts twee punten van die grafiek bevat. Voor punten op het verticale lijnstuk kun je inzien dat elk klein schijfje de verzameling snijdt in twee convergente rijen (zie figuur 3). (Ook hier: je moet er oneindig veel lijntjes bij denken.) In beide gevallen zitten daar alléén éénpuntige continua in. Onze verzameling is dus een kromme.

Waarom is deze kromme bedacht? Om te laten zien dat er krommen zijn die je niet continu kunt doorlopen. Een ‘normale’ kromme, zoals een cirkel of een lemniscaat, heeft de eigenschap dat je voor elk tweetal punten, $a$ en $b$, een continue functie, $f$, van [0, 1] naar de kromme kunt maken met $f(0) = a$ en $f(1) = b$. Voor onze kromme $S$ kan dat niet altijd. Neem maar $a = (–1, –\sin 1)$ en $b = (0, 0)$ en stel dat $f: [0, 1] → S$ continu is met $f(0) = a$ en $f(1) = b$. Maar, wegens de samenhang moet het volgende gebeuren: er is een $t_1$ met $f(t_1) = (–1/π, 0)$, er is een $t_2 > t_1$ met $f(t_2) = (–2/π, 0)$, er is een $t_3 > t_2$ met $f(t_3) = (–3/π, 0)$, enzovoort.

Maar dan moet er voor elke $n$ een $s_n$ zijn met $t_{2n} < s_n < t_{2n+1}$ en $f(s_n) = (–1/((2n + 1/2)π), –1)$, want als je binnen $S$ van $f(t_{2n})$ naar $f(t_{2n+1})$ gaat, kom je langs dat punt. De stijgende rij van de $t_n$-en heeft een limiet; noem die $t$. Wegens de continuïteit geldt $f(t) = lim_{n→∞} f(t_n) = (0, 0)$, en ook $f(t) = lim_{n→∞} f(s_n) = (0, –1)$ en dat kan niet samengaan. Zo’n verbindende functie $f$ bestaat dus niet.

Poolse cirkel

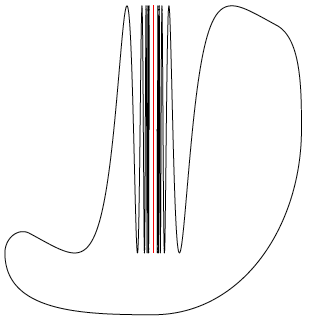
De Poolse cirkel, $P$, maken we door aan $S$ een paar lijnstukken toe te voegen die (–1, –sin 1) en (0, –1) verbinden: bijvoorbeeld van (–1, –sin 1) recht naar beneden naar (–1, –2), dan recht naar (0, –2) en ten slotte recht omhoog naar (0, –1) (zie figuur 4).

In het logo is de ‘cirkel’ wat vloeiender getekend, maar voor de eigenschappen van de kromme maakt dat niet echt uit. Door de extra lijnstukken kun je nu wel elk tweetal punten met een continue functie $f: [0, 1] → P$ verbinden, maar aan de andere kant kun je deze kromme niet in één pennenstreek tekenen: er is geen continue functie $f: [0, 1] → P$ (de pennenstreek) die elk punt bereikt. Het bewijs stond eigenlijk al in de vorige paragraaf, want die ene pennenstreek zou ook $a$ en $b$ binnen $S$ moeten verbinden en dat gaat niet.

Waarom noemen we dit de Poolse (of Warschause) cirkel? In de jaren ’20 en ’30 van de vorige eeuw werd in Polen veel onderzoek naar krommen in het platte vlak gedaan. Dit voorbeeld werd vaak gebruikt om vermoedens te testen: ‘zou het zo kunnen zijn dat elke kromme die of die eigenschap heeft?’, of ‘laten we eerst eens naar de $\sin(1/x)$- kromme kijken.’ Hieronder maken we een variant op de cirkel die laat zien dat het begrip ‘rand van een gebied’ niet zo eenvoudig is als je misschien denkt.

Nog een ‘cirkel’

Je kunt het plaatje ook wat symmetrischer maken: begin met $S$ en doe daar ook de grafiek van $\sin(1/x)$ voor $0 < x ≤ 1$ bij. Verbind dan de punten (–1, –sin 1) en (1, sin 1) met rechte lijnstukken, of een mooie vloeiende kromme. Nu krijg je weer iets wat op een cirkel lijkt, met een binnen- en buitengebied. Hier is iets geks mee aan de hand: het verticale lijnstuk $V$ ligt op de rand van die twee gebieden: als $x$ een element is van $V$, dan bevat elk schijfje om x punten van beide gebieden. De punten van V zijn echter vanuit beide onbereikbaar. Je kunt niet een continue functie, $f$, maken met domein [0, 1] en wel zo dat $f(t)$ voor $t < 1$ in het binnengebied ligt en met $f(1)$ in $V$, en idem voor het buitengebied. De heen en weer slingerende $\sin(1/x)$ zorgt daar voor (zie figuur 5 en 6).

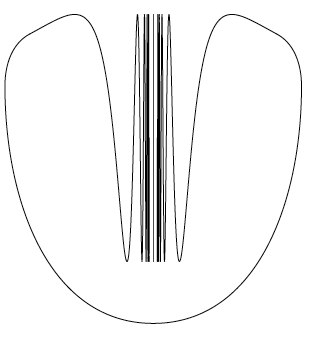
Bij een gewone cirkel is elk punt van beide kanten bereikbaar, zelfs met behulp van een recht lijntje. Dit voorbeeld (en vele andere trouwens ook) laat zien dat je in de topologie erg moet oppassen met je intu.tie, in dit geval dus bij het begrip ‘rand’. Wat voor de hand lijkt te liggen omdat je het bij zoveel gebieden ziet gebeuren – namelijk dat elk punt op de rand bereikbaar is – hoeft in het algemeen niet geldig te zijn. Je kunt kennelijk gebieden maken met heel rare randen. Met heel veel puzzelwerk kun je bijvoorbeeld een familie van drie disjuncte gebieden maken die alle drie precies dezelfde rand hebben. En met nog meer werk kun je een oneindige familie onderling disjuncte gebieden maken, allemaal met exact dezelfde rand. Zoek op internet maar eens naar ‘de meren van Wada’ (in het Engels ‘the lakes of Wada’), waarover we ook al eens schreven in dit tijdschrift (Pythagoras 44-2, november 2004).