De geconstrueerde rangschikking van de elementen van $\mathbb{Q}$ was echter niet zo mooi, aangezien ieder getal in $\mathbb{Q}$ oneindig vaak in de lijst voorkwam.

Tellen met behulp van een boom

De nieuwe manier van tellen van Calkin en Wilf is veel minder bekend dan het feit dat er aftelbaar veel rationale getallen zijn. Zij construeerden een nette bijectie, een één-op-één correspondentie, tussen $\mathbb{Q}$ en $\mathbb{N}$. Hun methode is gebaseerd op een graaf of boom die alle positieve rationale getallen precies een keer bevat. Die boom staat nu bekend als de Calkin-Wilf boom, maar werd eerder ook al door anderen gebruikt, in het bijzonder door Kepler die een deel van de graaf in zijn werk Harmonices Mundi uit 1619 tekende. Zie figuur 1. Iedere regel bevat vertakkingen van de regel erboven: een 'ouder'-breuk heeft twee 'kinderen', eentje met dezelfde teller en eentje met dezelfde noemer. Een breuk $\frac{a}{b}$ in de boom heeft kinderen $\frac{a}{a+b}$ en $\frac{a + b}{b}$. Hieruit volgt meteen dat alle breuken in de boom onvereenvoudigbaar zijn, want $ggd(a,a + b) =ggd (a + b,b) = 1$.

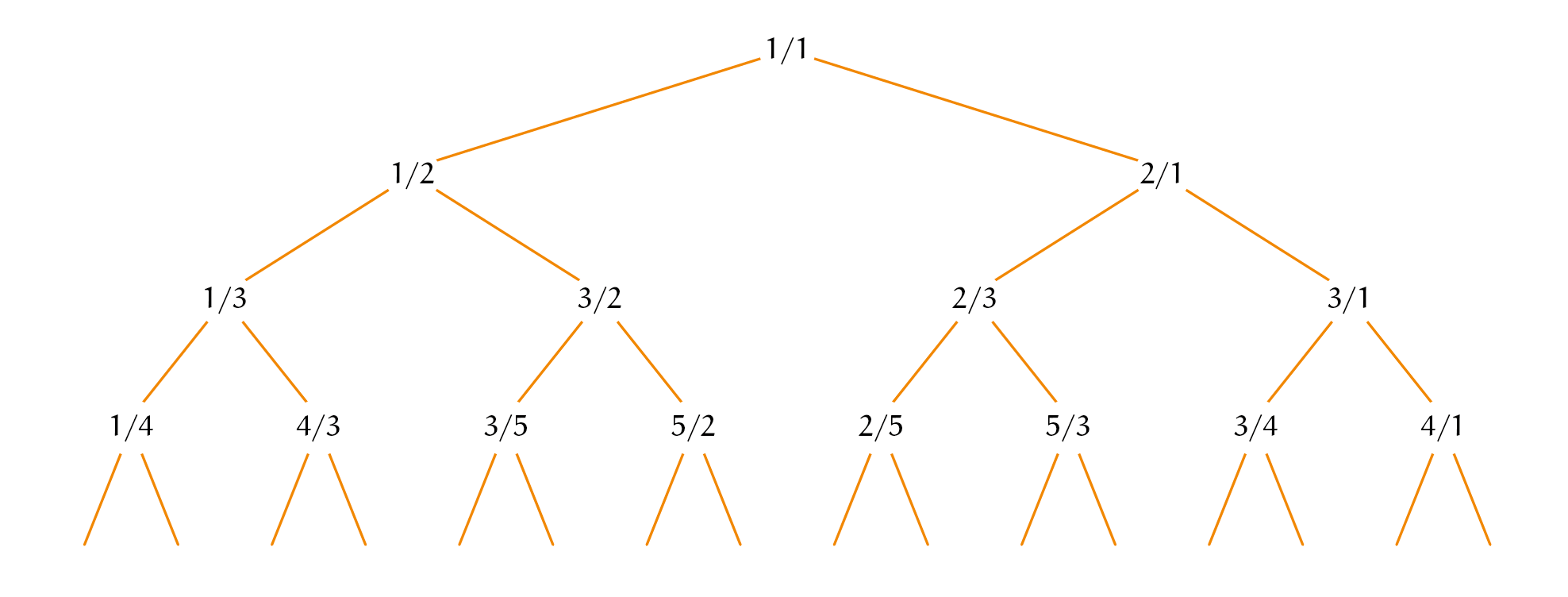Figuur 1 - De pagina in Keplers werk en de Calkin-Wilf boom

De bewering van Calkin en Wilf is, dat je precies één keer langs ieder positief element van $\mathbb{Q}$ komt als je van boven naar beneden en van links naar rechts door deze boom wandelt. Vervolgens kun je heen en weer springen tussen positieve en negatieve elementen zoals dat ook bij het tellen van $\mathbb{Z}$ gebeurt. Dus met een lijst die alle positieve rationale getallen bevat zijn we tevreden.

De lijst van Calkin en Wilf begint als volgt:

$\frac{1}{1}$, $\frac{1}{2}$, $\frac{2}{1}$, $\frac{1}{3}$, $\frac{3}{2}$, $\frac{2}{3}$, $\frac{3}{1}$, $\frac{1}{4}$, $\frac{4}{3}$, $\frac{3}{5}$, $\frac{5}{2}$, $\frac{2}{5}$, $\frac{5}{3}$, $\frac{3}{4}$, $\frac{4}{1}$, $\frac{1}{5}$, $\frac{5}{4}$, $\frac{4}{7}, \ldots$

Een eerste eigenschap van de rij die meteen opvalt, is dat de teller van iedere breuk gelijk is aan de noemer van de vorige. Om een rangnummer toe te kennen aan iedere breuk in de lijst maken Calkin en Wilf hier gebruik van. Zij schrijven iedere breuk als $\frac{b(n)}{b(n+1)}$, waarbij de getallen $b(n)$ gegeven worden door de lijst

$\{1,1,2,1,3,2,3,1,4,3,5,2,5,3,4,1,5,4,7,\dots\}$

En het blijkt dat ieder getal $b(n)$ het aantal manieren is waarop je het getal $n$ als de som van machten van $2$ kunt schrijven, waarbij iedere macht hooguit twee maal wordt gebruikt. Zo is bijvoorbeeld $6 = 4 + 2 = 4 + 1 + 1 = 2 + 2 + 1 + 1$, dus $b(6) = 3$. Dit heet het aantal hyperbinaire representaties van $6$. In het artikel wordt bewezen dat de resulterende afbeelding $n \leftrightarrow \frac{b(n)}{b(n + 1)}$ een bijectie van $\mathbb{N} \to \mathbb{Q}^+$ is die ieder positief element van $\mathbb{Q}$ precies één keer telt.

Opgave 1 Bepaal zelf $b(10)$, $b(13)$ en $b(18)$.

Het rangnummer van een breuk vinden

Het is niet zo makkelijk om de getallen $b(n)$ te vinden zonder verdere kennis. Maar een equivalente manier om door de lijst te lopen is wel relatief eenvoudig uit te voeren. Er is een simpele functie, namelijk

$$f(x)=\frac{1}{2\lfloor x\rfloor+1-x}$$

die de lijst met alle onvereenvoudigbare breuken op een recurrente manier genereert. Hierin is $\lfloor x\rfloor$ de entier van $x$, het gehele deel van $x$. Bijvoorbeeld $\left\lfloor\frac{5}{4}\right\rfloor=1$ en $\left\lfloor\frac{7}{3}\right\rfloor = 2$.

Voor deze $f$ geldt:

	$f(x)$	$=$	$\frac{1}{1-x}$ voor $0\le x < 1$
	$f(x+1)$	$=$	$\frac{f(x)}{f(x)+1}$

De functie $f$ wordt hierdoor volledig vastgelegd. Definieer nu de rij $(x_i)$ door

$x_0 = 1/1 = 1$  en  $x_{i+1} = f(x_i)$.

We kunnen nu de eerste getallen in de rij genereren:

$x_1=f(1)=\frac{1}{2\cdot 1+1-1}=\frac{1}{2}$,
$x_2=f(\tfrac{1}{2})=\frac{1}{2\cdot 0+1-\tfrac{1}{2}}=\frac{2}{1}$,
$x_3=f(2)=\frac{1}{2\cdot 2+1-2}=\frac{1}{3}$.

Opgave 2 Bepaal zelf enkele volgende getallen in de lijst en controleer of ze overeenkomen met de lijst die op basis van de boom was geconstrueerd.

Dat de eerste getallen in de lijst correct zijn is natuurlijk geen bewijs dat de functie $f$ inderdaad precies de gewenste lijst genereert. Met behulp van de eigenschappen voor $f$ kun je met volledige inductie bewijzen dat de rij $(x_i)$ voldoet aan twee regels:

	$x_{2i+2}$	$=$	$x_i+1$		($\color{crimson}{a}$)
	$x_{2i+1}$	$=$	$\frac{x_i}{x_i+1}$		($\color{crimson}{b}$)

Hiermee kunnen we aan de slag. Als je bijvoorbeeld weet dat $x_{10}=\frac{5}{2}$, dan volgt daaruit dat

	$x_{22}$	$=$	$\frac{5}{2}+1=\frac{7}{2}$		($\color{crimson}{a}$) en
	$x_{21}$	$=$	$\frac{\tfrac{5}{2}}{\tfrac{5}{2}+1}=\frac{5}{7}$		($\color{crimson}{b}$).

Neem een willekeurige positieve $x$ in $\mathbb{Q}$. Schrijf $x$ als de eenvoudigste breuk: $x = \frac{p}{q}$ met $ggd(p, q) = 1$. We maken nu een rijtje met getallen dat omhoog loopt door de boom, dus voor iedere breuk $\frac{p}{q}$ bepalen we de 'ouder'. Dit kan met het volgende algoritme:

($\color{crimson}{i}$)	als $p\ge q$ dan is de volgende breuk $\frac{p-q}{q}$;
($\color{crimson}{ii}$)	als $q > p$ dan is de volgende breuk $\frac{p}{q-p}$;
($\color{crimson}{iii}$)	herhaal stappen ($\color{crimson}{i}$) en ($\color{crimson}{ii}$) tot je op $1$ uitkomt.

We werken twee voorbeelden uit, te beginnen met $\frac{15}{37}$. Het rijtje wordt dan:

$\frac{15}{37}$, $\frac{15}{22}$, $\frac{15}{7}$, $\frac{8}{7}$, $\frac{1}{7}$, $\frac{1}{6}$, $\frac{1}{5}$, $\frac{1}{4}$, $\frac{1}{3}$, $\frac{1}{2}$, $\frac{1}{1}$.

Het begingetal $\frac{32}{17}$ leidt tot:

$\frac{32}{17}$, $\frac{15}{17}$, $\frac{15}{2}$, $\frac{13}{2}$, $\frac{11}{2}$, $\frac{9}{2}$, $\frac{7}{2}$, $\frac{5}{2}$, $\frac{3}{2}$, $\frac{1}{2}$, $\frac{1}{1}$.

Als je Euclides' algoritme voor het bepalen van de grootste gemene deler kent, zul je dat in deze voorbeelden herkend hebben. Van de rijtjes getallen kunnen we nu met behulp van regels ($\color{crimson}{a}$) en ($\color{crimson}{b}$) de rangnummers bepalen door in omgekeerde richting te werken, beginnend met $x_0 = 1$: zie tabel.

$\color{white}{breuk}$	$\color{white}{nummer}$	$\color{white}{regel}$		$\color{white}{breuk}$	$\color{white}{nummer}$	$\color{white}{regel}$
$\frac{1}{1}$	$0$	-		$\frac{1}{1}$	$0$	-
$\frac{1}{2}$	$1$	($\color{crimson}{b}$)		$\frac{1}{2}$	$1$	($\color{crimson}{b}$)
$\frac{1}{3}$	$3$	($\color{crimson}{b}$)		$\frac{3}{2}$	$4$	($\color{crimson}{a}$)
$\frac{1}{4}$	$7$	($\color{crimson}{b}$)		$\frac{5}{2}$	$10$	($\color{crimson}{a}$)
$\frac{1}{5}$	$15$	($\color{crimson}{b}$)		$\frac{7}{2}$	$22$	($\color{crimson}{a}$)
$\frac{1}{6}$	$31$	($\color{crimson}{b}$)		$\frac{9}{2}$	$64$	($\color{crimson}{a}$)
$\frac{1}{7}$	$63$	($\color{crimson}{b}$)		$\frac{11}{2}$	$94$	($\color{crimson}{a}$)
$\frac{8}{7}$	$128$	($\color{crimson}{a}$)		$\frac{13}{2}$	$190$	($\color{crimson}{a}$)
$\frac{15}{7}$	$258$	($\color{crimson}{a}$)		$\frac{15}{2}$	$382$	($\color{crimson}{a}$)
$\frac{15}{22}$	$517$	($\color{crimson}{b}$)		$\frac{15}{17}$	$765$	($\color{crimson}{b}$)
$\frac{15}{37}$	$1035$	($\color{crimson}{b}$)		$\frac{31}{17}$	$1532$	($\color{crimson}{b}$)

Je ziet dat elke stap met regel ($\color{crimson}{a}$) of ($\color{crimson}{b}$) ongeveer een verdubbeling van het rangnummer geeft, wat dus snel hoge posities in de lijst oplevert, zelfs voor breuken met relatief kleine getallen in de teller en noemer. Dat correspondeert dan toch weer met het gevoel dat er erg veel rationale getallen zijn: voor een willekeurig gekozen positief element van $\mathbb{Q}$ moet je waarschijnlijk erg lang tellen om het te bereiken. Maar je zult er wel in een eindige hoeveelheid tijd komen!