In het vorige artikel telden we de (priem) factoren van honderd willekeurige getallen van $18$ cijfers. Om toch in het algemeen iets te kunnen zeggen over $E_N$, het gemiddeld aantal factoren van een groot getal $N$, kijken we niet meer naar afzonderlijke getallen, maar gaan we rekenen met de kans dat een willekeurig getal $n$ een priemgetal is. Priemgetallen liggen, per stuk bekeken, weliswaar onregelmatig uitgestrooid over de getallenlijn, maar als je grote stukken getallenlijn bekijkt, voldoen ze toch aan statistische regels. Zo is al lang geleden bewezen dat de kans dat een getal $n$ priem is, ongeveer gelijk is aan $1/\ln(n)$, en hoe groter het getal, hoe beter dit klopt. Dit resultaat staat bekend als de Priemgetallenstelling.

De Priemgetallenstelling zegt het volgende: $$\pi(n) \sim \frac{n}{\ln(n)}.$$

Hierin is $\pi(n)$ het aantal priemgetallen tot en met $n$ en de relatie betekent dat

$$\lim_{n\to\infty}\frac{n}{\pi(n)\cdot\ln(n)}=1.$$

De stelling werd onafhankelijk geformuleerd door Legendre en Gauss na bestudering van tabellen met priemgetallen. De stelling is uiteindelijk bewezen door Hadamard en De la Vallée Poussin. Het bewijs is niet makkelijk en vergt veel kennis van complexe functietheorie.

Dus rond het getal duizend zijn ongeveer $ 1$ op de $\ln(1000)$ getallen priem, dat is afgerond $7$, rond de miljard is dat ongeveer $ 1$ op de $\ln(1.000.000.000)$, ongeveer $20 $. Een getal van $18$ cijfers heeft een kans van ongeveer $1$ op $40$ om priem te zijn.

We zagen eerder dat een groot getal $N $ van elk kleiner priemgetal $p$ gemiddeld $ \frac{1}{(p - 1)}$ factoren $p$ bevat. En als we een lijst hadden van al die $p$-tjes dan konden we al die termen $\frac{1}{(p - 1)}$ bij elkaar optellen, en dan wisten we $E_N$, het verwachte aantal priemfactoren dat een getal $N $ gemiddeld bevat. Voor alle $p<1000 $ hebben we die som in het vorige artikel daadwerkelijk bepaald.

Voor grotere $p$ maken we een benadering. Hoe we dat doen laten we zien rond het getal $1000$. De eerste twee priemgetallen na $1000$ zijn $1009$ en $1013$. Die leveren dus een bijdrage van $\frac{1}{1008} + \frac{1}{1012} = 0{,}0019802$ aan $E_N$. Maar stel nu dat we niet weten wat die eerste twee priemgetallen zijn; we weten wel dat ongeveer $ 1$ op de $7$ getallen priem is.
Dat gebruiken we als volgt: we gokken dat één van de getallen $1001$ tot en met $1007 $ priem is en ook één van de getallen $1008 $ tot en met $1014$, maar we weten dus niet welke. De bijdrage van die twee onbekende priemgetallen aan $E_N$ benaderen we dan met de som van de gemiddelden 

$$\frac17\left(\frac{1}{1000}+\frac{1}{1001}+\cdots+\frac{1}{1006}\right)$$

en

$$\frac17\left(\frac{1}{1007}+\frac{1}{1008}+\cdots+\frac{1}{1013}\right)$$

en dat is ongeveer $0{,}0019871$. Deze benaderde bijdrage aan $E_N$ valt dus iets te hoog uit, omdat de twee priemgetallen $1009$ en $1013$ allebei in het tweede interval, $[1007, 1014]$, zitten.

Maar als je een groot stuk van de getallenlijn, van $A$ tot $B$, op deze manier opknipt in veel kleine intervalletjes, middelt de onregelmatige verdeling van de priemgetallen uit en krijg je een goede benadering van wat dat stuk getallenlijn bijdraagt aan $E_N$.

De volgende stap is dan om niet naar de som van de $\frac{1}{n-1}$ (met $A \le n \le B$) te kijken, maar om die som met een integraal te benaderen.

Dat is gebruikelijk in de getaltheorie; de integraal geeft vaak een mooie formule en men kan meestal goed aangeven hoe groot het verschil tussen de mooie formule en het echte antwoord maximaal kan zijn. In ons geval benaderen we de bijdrage van het interval $[A, B]$ aan $E_N$ met

$$\int_A^B \frac{1}{(x-1)\ln(x)}\mbox{d}x$$

Verder hebben we alles voor x < $x < 1000$ al met de hand uitgerekend en voor grote x $x$ is $x-1$ is x ongeveer gelijk aan $x;$ we bekijken $ $ daarom deze integraal

$$\int_A^B\frac{1}{x\ln(x)}\mbox{d}x$$

Die is namelijk makkelijk uit te rekenen:

$$\int_A^B\frac{1}{x\ln(x)}\mbox{d}x = \ln(\ln(B))-\ln(\ln(A))$$

$(\dagger)$

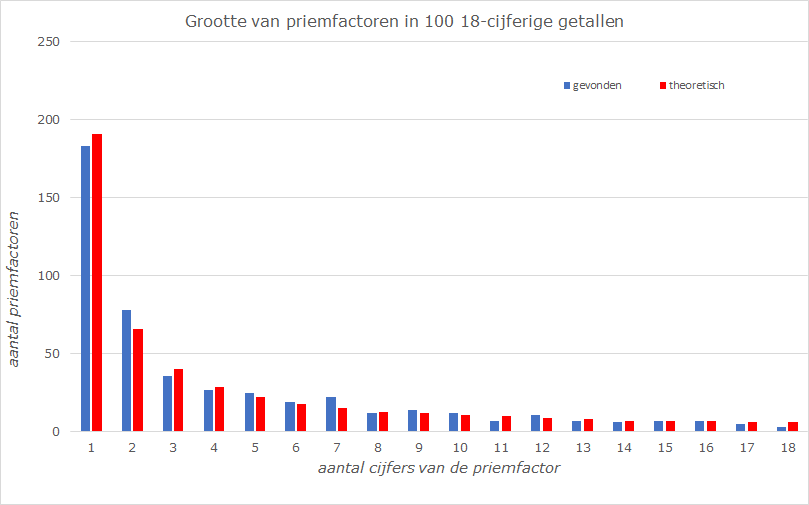
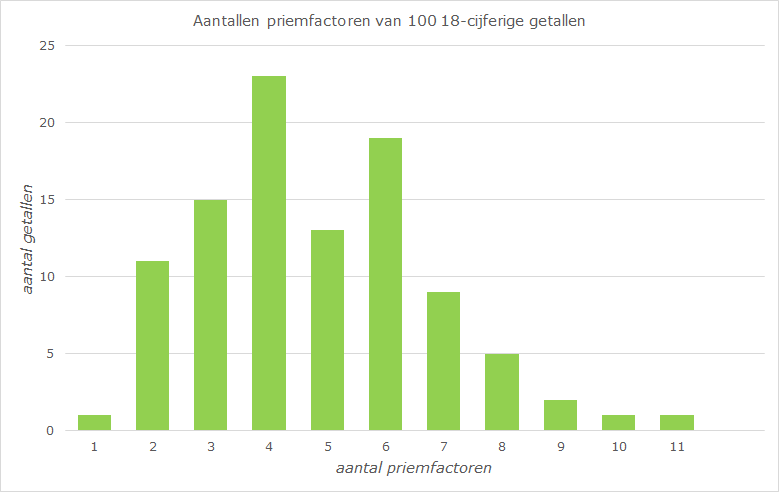
We kunnen dit nu vergelijken met onze steekproef. Grafiek 1 laat zien dat de honderd getallen samen $481$ factoren hebben $(183 + 78 + 36 + \cdots = 481)$. Anderzijds, je kunt ook de factoren tellen in grafiek 2: er zijn vier getallen met maar één factor, zes getallen met twee factoren, enzovoort, dus in totaal $ 1\cdot 1 + 11\cdot 2 + 15\cdot 3 + \cdots = 481$ · · · factoren. Op beide manieren vinden we dat een getal van $18$ cijfers gemiddeld $4{,}8 $ factoren heeft.

We hebben al gezien, dat in theorie de getallenlijn van $2$ tot $1000$ een bijdrage van $2{,}97$ factoren levert. We gebruiken nu formule $(\dagger)$ om de rest van de getallenlijn in rekening te brengen. Omdat een 18-cijfergetal minimaal $10^{17}$ is, en maximaal $10^{18} - 1$, bekijken we beide uitersten, afgerond op twee decimalen: $\ln(\ln(10^{17})) = 3{,}67$ en $\ln(\ln(10^{18} - 1)) = 3{,}72$. We vatten dit samen als $3{,}70\ (\pm 0{,}02)$. Dus de bijdrage van de getallenlijn vanaf $1000$ is:

$$3{,}70 - \ln(\ln(10^3)) = 3{,}70 - 1{,}93 = 1{,}77.$$

Samen met de bijdrage van de priemgetallen onder de $1000$ wordt dit $2{,}97 + 1{,}77 = 4{,}74$.

Theoretisch is het aantal factoren van een 18-cijfergetal dus $4{,}74 (\pm 0{,}02)$ terwijl de steekproef de experimentele waarde $4{,}8 $ geeft. Als we te lui waren geweest om de bijdrage van de priemgetallen van $10$ tot $1000$ handmatig uit te werken dan hadden we die ook mee kunnen nemen in de integraalformule. Dan krijgen we

$$\begin{array}{l}1{,}99 + 3{,}70 - \ln(\ln(10)) =\\
1{,}99 + 3{,}70 - 0{,}83 = 4{,}86\end{array}$$

($1{,}99$ is de bijdrage van de factoren $2$, $3$, $5$,  en $7$). Ook dat klopt nog redelijk.

Als we met blind vertrouwen in formule $(\dagger)$ zelfs de bijdragen van $2$, $3$, $5$ en $7$ niet afzonderlijk hadden uitgerekend, dan wordt het $3{,}70 - \ln(\ln(2)) = 3{,}70 - (-0{,}37) = 4{,}07$.

Het zijn dus vooral de bijdragen van de heel kleine priemgetallen die voor afwijkingen van de formule $\ln(\ln(x))$ zorgen.

We kunnen in formule $(\dagger)$ ook het kleinste en grootste getal van een zeker aantal cijfers kiezen, bijvoorbeeld $1000$ en $9999$, en theoretisch voorspellen hoeveel factoren vier cijfers hebben: $\ln(\ln(9999)) - \ln(\ln(1000)) \approx 0{,}29$. Dus op een steekproef van honderd getallen verwachten we $29$ factoren met vier cijfers. Voor alle aantallen cijfers is dit uitgerekend en in rood in grafiek 1 aangegeven.

De voorspelling op grond van formule $(\dagger)$ komt behoorlijk goed overeen met de waarden in de steekproef. We hebben dus een theoretische manier gevonden om het gemiddeld aantal factoren van een getal met $N$ cijfers te vinden.

Uiteraard is eerder onderzocht hoeveel factoren een groot getal $N$ heeft. Een formule daarvoor vind je bijvoorbeeld op mathworld.wolfram.com/PrimeFactor.html. De eerste term van die formule is inderdaad $\ln(\ln(N))$, gevolgd door een constante en dan een nogal ingewikkelde oneindige som. Als je zin hebt in verder onderzoek: is ook de verdeling van de aantallen factoren in grafiek 2 theoretisch te verklaren? Het meest waarschijnlijk ($25\%$ kans) is, dat een getal van $18$ cijfers vier factoren heeft, en naar beide kanten (minder of meer dan vier factoren) neemt die kans snel af. We hebben al gezien dat er een benaderingsformule is voor het aantal priemgetallen kleiner dan $N$ als $N$ groot is. In principe kun je dan ook het aantal ‘dipriemen’ (getallen met precies twee factoren) kleiner dan $N$ berekenen. Maar dit wordt toch al snel ingewikkeld, en de berekening van het aantal tripriemen, enzovoort is nog veel onoverzichtelijker.

Op de Wikipediapagina Divergence of the sum of the reciprocals of the primes kun je lezen dat de benadering $\ln(\ln(N))$ voor de som

$$\sum_{p\le N}\frac{1}{p-1}$$

zo gek nog niet is.

Het verschil

$$\sum_{p\le N}\frac{1}{p-1}-\ln(\ln(N))$$

converteert naar een vast getal. En zoals in het artikel aangegeven komt dat verschil vooral door de afwijkingen bij de kleine priemgetallen.