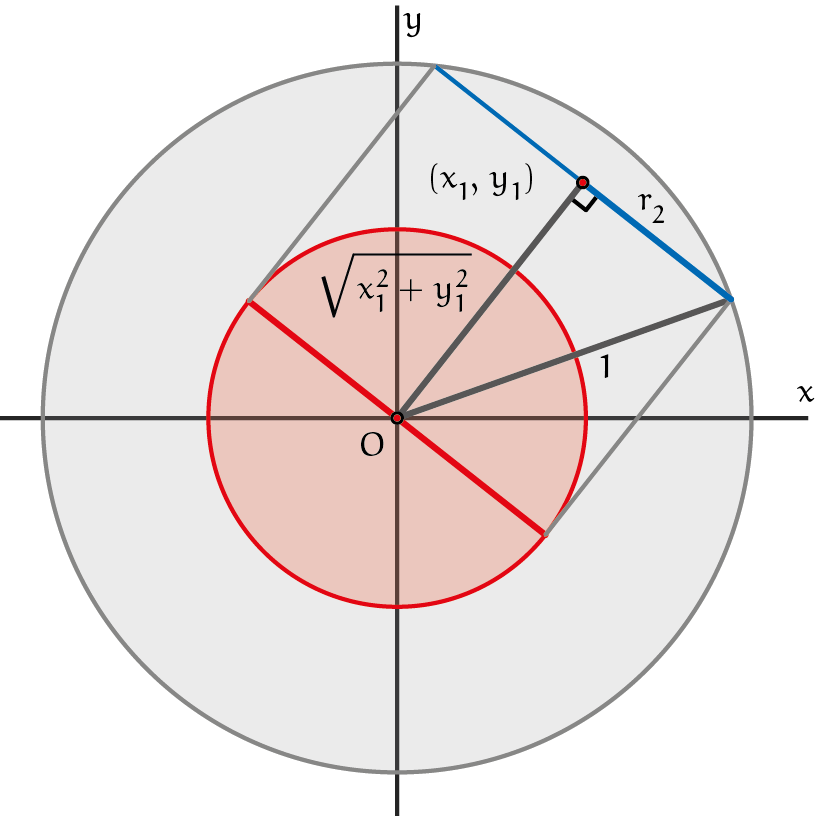Australisch science fiction schrijver en programmeur Greg Egan bedacht in augustus 2019 het spel HyperDarts. Na enige discussie was het spel geherformuleerd tot een wiskundig handig te beschrijven spel. Hyperdarts start met een bull's eye met straal $1$. Met iedere dart die landt, neemt de doorsnede af tot de lengte van de koorde waar de dart op ligt loodrecht op de straal door de dart (het blauwe lijnstuk in de figuur rechts is een koorde, de nieuwe straal van de cirkel wordt dan de helft daarvan, $r_2$). Als de dart buiten de bull's eye terechtkomt, dan wordt de nieuwe doorsnede $0$. Neem aan dat een dartspeler met gelijke kans een willekeurig punt in een vierkant met zijden $2$ waarbinnen het dartbord hangt kan raken. De score $S$ van de speler is het totaal aantal geworpen dartpijlen tot het spel eindigt doordat hij buiten de dan geldende bull's eye gooit. De minimumscore is dus $1$. De vraag is nu: als spelers een oneindig aantal darts mogen gooien, wat is dan de verwachte score?

Wat in eerste instantie een lastig te analyseren probleem lijkt, blijkt op een heel elegante manier opgelost te kunnen worden. Iedere keer kan de kans om weer raak te gooien worden uitgerekend op basis van het volume van een hoger-dimensionale eenheidsbol. De verwachtingswaarde wordt gegeven door een bekende oneindige som. We leggen hier uit hoe een gewoon dartbord kan leiden tot volumes van n-dimensionale bollen. Op 3blue1brown. com maakte Grant Sanderson er een videoles over.

De eerste en de tweede worp

Het spel begint met een cirkel met straal $r_1 = 1$ rond de oorsprong als start-dartbord en gaat uit van een speler die met een uniforme kansverdeling op een vierkant bord gooit, met coördinaten $(x, y)$ met $-1 \le x \le 1$ en $-1 \le y \le 1$. De kans dat de eerste pijl de cirkel raakt kun je uitrekenen met behulp van oppervlaktes (zie ook Pythagoras 62-3 'Wat is de kans op een stompe driehoek?'). Omdat aangenomen wordt dat de speler ieder plekje binnen het vierkant met een even grote kans raakt, bepaalt de verhouding tussen de oppervlakte van de cirkel en de totale oppervlakte van het vierkant de kans om de cirkel te raken. Laat $(x_1, y_1)$ het landingspunt van de eerste dartpijl zijn. De kans dat pijl $1$ in de cirkel terechtkomt is dan

$$P(x_1^2+y_1^2\le 1)=\frac{\rm opp.\ cirkel}{\rm opp.\ vierkant}=\frac{\pi}{4}.$$

Als de eerste pijl raak wordt gegooid, wordt de eindscore $S$ tenminste gelijk aan $2$: $S = 2$ als de tweede pijl mis gaat en $S \ge 3$ als de tweede pijl ook raak is. We weten nu dus dat $P(S \ge 2)=\frac{\pi}{4}$.

Zoals gezegd wordt het dartbord nu aangepast: pijl $2$ zal 'raak' zijn als hij binnen een cirkel terechtkomt waarvan de diameter gelijk is aan de lengte van de koorde door $(x_1, y_1)$. Met behulp van de stelling van Pythagoras vinden we voor de nieuwe straal $r_2$ dat

$$r_2^2+\left(\sqrt{x_1^2+y_1^2}\right)^2=r_1^2=1.$$

Zie de figuur. De kans dat de tweede dartpijl landt in een punt $(x_2, y_2)$ binnen de nieuwe, kleinere cirkel is daarmee

$$P(x_2^2+y_2^2\le r_2^2)=P(x_2^2+y_2^2\le 1-x_1^2-y_1^2)=P(x_1^2+y_1^2+x_2^2+y_2^2\le1)$$

en deze kans is gelijk aan P(S ≥ 3).

Een bol in vier dimensies

Laten we nu even vergeten dat $(x_1, y_1)$ en $(x_2, y_2)$ de coördinaten van twee punten in het vlak zijn. Je kunt $(x_1, y_1, x_2, y_2)$ namelijk
ook als een punt in een vierdimensionale ruimte beschouwen. En in een vierdimensionale ruimte definieert $x_1^2+y_1^2+x_2^2+y_2^2\le1$ precies de eenheidsbol! Daarmee is de kans $P(x_1^2+y_1^2+x_2^2+y_2^2\le1)$ gelijk aan de verhouding tussen het 'volume' $V_4$ van de vierdimensionale bol met straal $1$ en het 'volume' van de 4D hyperkubus met zijden $2$:

$$P(x_1^2+y_1^2+x_2^2+y_2^2\le1)=\frac{V_4}{2^4}.$$

Volgende pijlen

Het punt $(x_2, y_2)$ bepaalt de straal $r_3$ van de cirkel waarbinnen het landingspunt $(x_3, y_3)$ van pijl $3$ moet vallen om 'raak' te zijn. Net als voor $r_2$ vinden we voor $r_3$ dat

$$r_3^2=\left(\sqrt{x_2^2+y_2^2} \right)^2=r_2^2$$

en daarmee is

$$\begin{align}P(S\ge4)&=P(x_3^2+y_3^2\le r_3^2)\\
&=P(x_3^2+y_3^2\le r_2^2-x_2^2-y_2^2)\\
&=P(x_3^2+y_3^2+x_2^2+y_2^2\le r_2^2)\\
&=P(x_1^2+y_1^2+x_2^2+y_2^2+x_3^2+y_3^2\le 1).
\end{align}$$

Net als voor de vorige kans vinden we dus dat

$$P(S\ge 4)=P(x_1^2+y_1^2+x_2^2+y_2^2+x_3^2+y_3^2\le 1)=\frac{V_6}{2^6}$$

als we $(x_1, y_1, x_2, y_2, x_3, y_3)$ als een punt in een zes-dimensionale ruimte beschouwen. Deze constructie kan worden doorgezet zolang pijlen binnen de dan geldende cirkel terechtkomen, en de score $S$ voldoet hiermee aan

$$P(S\ge s)=\frac{V_{2s-2}}{2^{2s-2}}.$$

In Pythagoras 60-4 (april 2021) werd in het artikel '3 Dimensies; Of Niet?' voor het volume $V_N$ van een $N$-dimensionale bol met straal $1$ aangetoond dat $V_0 = 1$, $V_1 = 2$ en $V_N=\frac{2\pi}{N}V_{N-2}$. We hebben hier alleen maar even dimensies $N = 2n$ nodig, waarvoor de recurrente betrekking leidt tot $V_{2n}=\frac{\pi^n}{n!}$.

Dit geeft

$$P(S \ge s) =\frac{\pi^{s-1}}{2^{2s-2}(s-1)!}=\left(\frac{\pi}{4}\right)^{s-1}\cdot\frac{1}{(s-1)!}.$$

De verwachte sCore

De verwachtingswaarde $\mathscr{E}(S)$ van $S$ is de eindscore die je gemiddeld verwacht. Deze is per definitie gelijk aan

$$\mathscr{E}(S) = P(S = 1) \cdot 1 + P(S = 2) \cdot 2 + P(S = 3) \cdot 3 + \cdots$$

We hebben hiervoor een formule gevonden voor $P(S \ge s)$, maar omdat de score steeds met $1$ toeneemt, geldt dat

$$P(S = s) = P(S \ge s) - P(S \ge s + 1).$$

Hiermee kunnen we $\mathscr{E}(S)$ herschrijven:

$$\begin{align}
\mathscr{E}(S)&=(P(S \ge 1) - P(S \ge 2)) \cdot 1\\
&+(P(S \ge 2) - P(S \ge 3)) \cdot 2 \\
&+(P(S \ge 3) - P(S \ge 4)) \cdot 3\\
&+\cdots\end{align}$$

Optellen en aftrekken leidt tot een balans: $\mathscr{E}(S) = P(S \ge 1) + P(S \ge 2) + P(S \ge 3) + \cdots$, zodat we met de eerder gevonden formule voor de kansen vinden dat

$$\mathscr{E}(S) =1+\frac{\pi}{4}+\left(\frac{\pi}{4}\right)^2\cdot\frac{1}{2!}+\left(\frac{\pi}{4}\right)^3\cdot\frac{1}{3!}+\cdots$$

Dit is precies gelijk aan de Taylorreeks voor $e^x$ voor de waarde $x = \frac{\pi}{4}$, zodat we uiteindelijk voor de verwachte score vinden dat $\mathscr{E}(S) = e^{\frac{\pi}{4}} \approx 2{,}1932$: als het spel vaak wordt herhaald, zou de gemiddeld behaalde score ongeveer $2{,}1932$ moeten zijn.