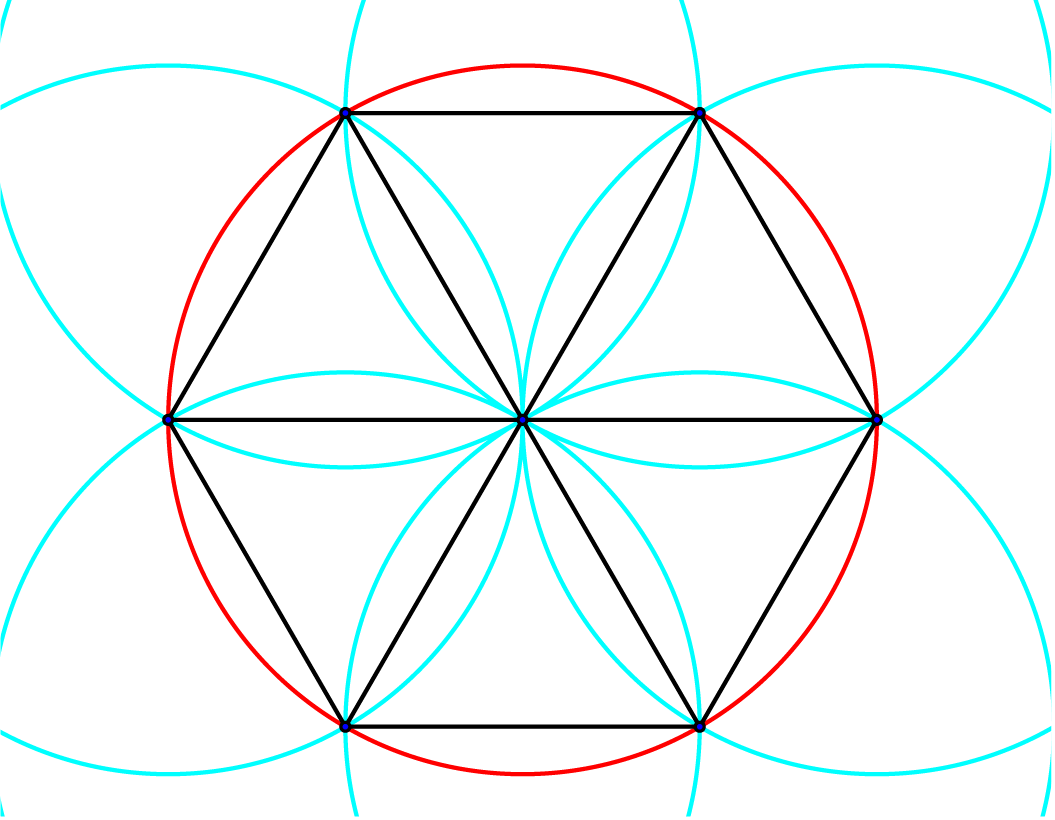
Neem als voorbeeld de constructie van een regelmatige zeshoek. Die constructie ken je vast wel: je tekent een cirkel en past de straal van die cirkel gewoon zes keer af op de cirkel. Dan kom je, als je het nauwkeurig gedaan hebt, weer bij het punt uit waar je op de cirkel begon. De zes punten die je zo krijgt vormen dan de regelmatige zeshoek (figuur 1). Het bewijs hiervan is eenvoudig genoeg en gebruikt alleen de eigenschap dat de som van de hoeken van een driehoek een gestrekte hoek is, oftewel $180^{\circ}.$

Figuur 1

Je ziet dat er zes identieke gelijkzijdige driehoeken ontstaan, waarvan de hoeken gelijk zijn aan $180^{\circ}  : 3 = 60^{\circ}.$ De hoekpunten in het middelpunt van de cirkel hiervan zijn dan samen $360^{\circ}.$ Dus het beginpunt valt samen met het eindpunt!

Is er ook een exacte constructie van de zevenhoek? Dat hangt ervan af wat voor hulpmiddelen je mag gebruiken. In Pythagoras 57-5/6 heb je kunnen lezen dat in de negentiende eeuw bewezen is dat het op de traditionele manier, met een passer en een liniaal (zonder schaalverdeling!) onmogelijk is.

Wat is een glijliniaalconstructie?

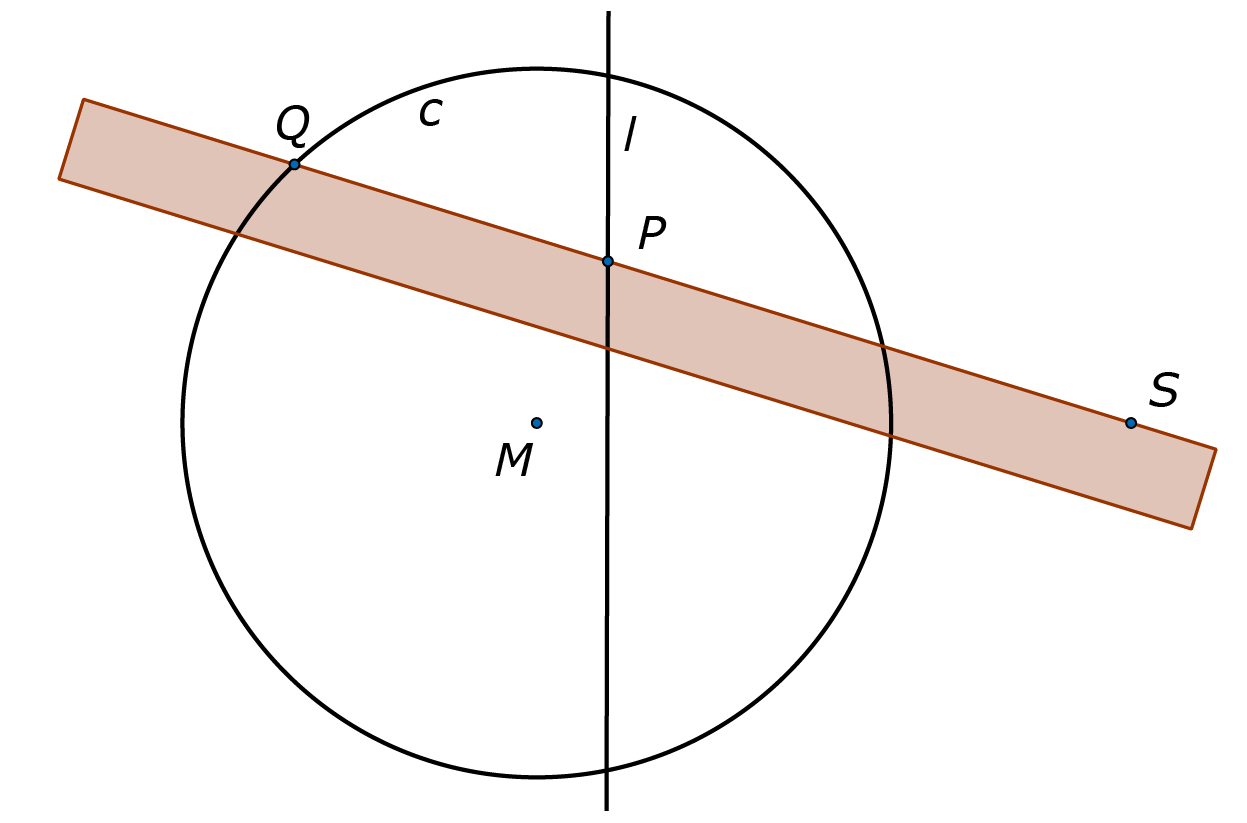
Toch zijn er wel manieren om de zevenhoek met passer en liniaal exact te construeren, maar dan moet je met je liniaal een beetje smokkelen: je mag er twee streepjes op zetten. In figuur 2 zie je een voorbeeld van hoe zo'n liniaal dan gebruikt mag worden. Gegeven zijn een cirkel met middelpunt $M,$ een lijn $l$ door de cirkel en een punt $S$ buiten de cirkel. We zoeken een punt $P$ op $l$ en $Q$ op de cirkel zodanig dat de afstand $PQ$ gelijk is aan de straal. Dat vergt wel wat geschuif en geglij, vandaar dat dit een glijliniaalconstructie genoemd wordt. De punten bij $P$ en $Q$ zijn dan de geconstrueerde punten.

Figuur 2

Een glijliniaalconstructie van de zevenhoek

In het boekje Das geheime Gesetz des Siebenecks (De geheime wet van de zevenhoek, figuur 3) van Hans Börnsen uit 1965 staan maar liefst tien verschillende glijliniaalconstructies. Met bewijs.

Figuur 3

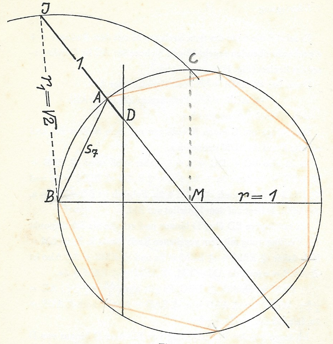
Hieronder zullen we de eerste van de tien bespreken. Zie figuur 4. Toevallig gebruikt de constructie dezelfde middelloodlijn van $BM$ en een punt op de cirkel met straal 1 als de benaderingsconstructie in het eerdere nummer van Pythagoras. Daarnaast wordt een cirkel met straal $\sqrt{2}$ gebruikt. Die kan je krijgen door een punt $C$ te construeren dat recht boven $M$ op de cirkel ligt, dus $\angle BMC = 90^{\circ}.$ Dan is $BC =\sqrt{2},$ volgens de stelling van Pythagoras.

Figuur 4

De constructie is eenvoudig. Teken een cirkel met middelpunt $M$ en een punt $B$ op de cirkel. Teken de middelloodlijn van $BM$ en de cirkel om $B$ met straal $\sqrt{2}.$ Zet nu twee streepjes op de liniaal waarvan de afstand gelijk is aan $1,$ de straal van de eerste cirkel. Dan leg je de liniaal zo neer dat  hij door $M$ gaat, het ene streepje (bij $D$) op de middelloodlijn en het andere streepje (bij $J$) op de cirkel met straal $\sqrt{2}$ ligt. Het punt waar de liniaal de cirkel snijdt noemen we $A$ en, hopla, daar hebben we de zijde van de zevenhoek: $AB.$ Als je deze nu vijf keer op de cirkel afpast heb je de andere hoekpunten van de zevenhoek!

En nu: het bewijs

Het bewijs is niet zo eenvoudig. Maar dat gaan we toch bekijken. Want in de wiskunde gaat het nu eenmaal om het bewijs. Zet je maar schrap!

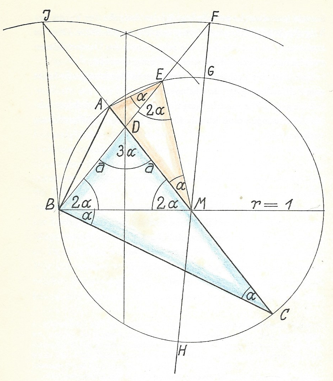
Zie figuur 5. Je ziet daarin onder andere de punten $D$ en $J$ van de vorige figuur terug. We gaan nu bewijzen dat als $AB$ een zijde van de zevenhoek is, dan is $DJ = 1.$

Figuur 5

Als $AB$ een zijde van de zevenhoek is, dan is $\angle AMB = 360^{\circ} : 7.$ Noem de helft van deze hoek $\alpha.$ Dus $\alpha = 180^{\circ} : 7$ en $\angle AMB = 2\alpha.$ Verleng $AM$ tot punt $C.$ Dan is $\Delta MBC$ gelijkbenig, zodat $\angle B = \angle C$ en $\angle B + \angle C = 180^{\circ}-\angle BMC = \angle BMA = 2\alpha.$ Dus $\angle B = \angle C=\alpha.$

Neem nu een punt $D$ op $AC$ waarvoor $CD = BC,$ zodat $\Delta BCD$ een gelijkbenige driehoek met tophoek $\alpha$ is. Omdat $\alpha = 180^{\circ} : 7$ is natuurlijk $7\alpha = 180^{\circ}.$ Dit zullen we in het vervolg vaak gebruiken. Bijvoorbeeld: $\angle CBD=\angle CDB = \frac{180^{\circ}-\alpha}{2}=\frac{7\alpha-\alpha}{2}=3\alpha.$ Daaruit volgt weer: $\angle DBM = 3\alpha-\alpha=2\alpha.$

Stel nu $MD = a.$ We gaan nog een heleboel andere hoeken en lijnstukken uitdrukken in $\alpha$ en $a.$

Omdat in $\Delta BDM$ geldt dat $\angle B=2\alpha$ en $\angle D=3\alpha$ moet $\angle M$ gelijk zijn aan $180^{\circ}-2\alpha-3\alpha=2\alpha.$ Oftewel: $\Delta BDM$ is gelijkbenig en $BD = MD$ en $D$ ligt op de middelloodlijn van $BM.$

We gaan verder. Verleng $BD$ tot deze de cirkel snijdt, daar komt punt $E.$ Omdat $\Delta BME$ gelijkbenig is volgt dat $\angle BEM=\angle EBM=2\alpha$ en $\angle EMB=3\alpha,$ waardoor $\angle EMA=\alpha.$ En omdat $\Delta AME$ ook gelijkbenig is volgt weer: $\angle AEM=\angle EAM=3\alpha$ en daarom $\angle AED=\alpha.$ Tenslotte, omdat in ∆ADE $\angle ADE=\angle BDM=3\alpha$ moet eveneens $\angle DAE=3\alpha$ en is ook ∆ADE gelijkbenig, met $AE = DE.$

Kijk nu naar de driehoeken $\Delta EAM$ (oranje) en $\Delta DBC$ (blauw). Die hebben dezelfde hoeken, ze zijn zoals dat heet: gelijkvormig. Daarom hebben de zijden dezelfde verhouding. Dus $\frac{AE}{AM}=\frac{BD}{CD}$ en $\frac{AE}{1}=\frac{a}{a+1},$ zodat $AE=\frac{a}{a+1}.$ Uit het voorgaande volgt dat dan ook $DE=\frac{a}{a+1}.$

We gaan weer een stapje verder. Stapje voor stapje komen we uiteindelijk uit op $DJ = 1,$ je zult het zien! We verlengen $BD$ nog wat verder: vanuit $D$ gaan we de eenheid verder, dat punt noemen we $F.$ Dus $DF = 1$ en $EF = 1 - DE = 1 -\frac{a}{a + 1} = \frac{a + 1}{a + 1} - \frac{a}{a + 1} = \frac{1}{a + 1}.$ Er komt zowaar nog wat algebra om de hoek kijken!

Verbindt nu $F$ met $M,$ waarmee de snijpunten $H$ en $G$ ontstaan. Volgens de machtsstelling (zie kader) geldt dan: $\frac{FE}{FG}=\frac{FH}{FB}$ waardoor:

$$\frac{\frac{1}{a+1}}{FM-1}=\frac{FM+1}{a+1}.$$

Kruislings vermenigvuldigen levert op: $1 = (FM - 1)(FM + 1) = FM^2 - 1,$ zodat $FM=\sqrt{2}.$

Nu zijn we er vrijwel! Als je de cirkel om $B$ met straal $\sqrt{2}$ bekijkt zie je de symmetrie in het figuur: als je $FM$ spiegelt in de middelloodlijn van $BM$ (het verticale lijntje waar $D$ op ligt) kom je in $BJ$ terecht. Maar dan moet $DJ$ wel gelijk zijn aan $FD$ en die lengte was de eenheid! Om dat helemaal hard te maken moet je kijken naar de congruente driehoeken $\Delta BMF$ en $\Delta MBJ.$ Probeer maar zelf. Conclusie: $DJ = 1.$  Om aan te tonen dat de glijliniaalconstructie klopt, moet je ook nog de omgekeerde redering bewijzen: als in de constructie in figuur 5 is gegeven dat $DJ = 1,$ bewijs dan dat $BA$ de zijde is van een regelmatige zevenhoek, ofwel dat $\alpha = 180/7.$ Je kunt dit bewijs zelf proberen; binnenkort verschijnt dat hier.

Ten slotte

Is deze glijliniaal constructie nu makkelijker uit te voeren dan de benaderingsconstructie? Ik denk het niet. Maar wiskundigen houden niet van benaderingen. Die willen exactheid en bewijzen! Als je eenvoudig een zevenhoek wilt tekenen kan je ook gewoon met je geodriehoek de hoeken van $360^{\circ} : 7 \approx 51{,}4^{\circ}$ in het middelpunt tekenen. Zo hebben de ontwerpers van de euromunt van 20 cent het vast gedaan (wist je dat daarin op de omtrek zeven inkepingen op gelijke afstand zitten, zodat blinden de munt kunnen herkennen?). En ook de ontwerper van de grafsteen van Gauss, waarop een regelmatige zeventienhoek gebeiteld staat, heeft het vast zo gedaan en niet met de constructie die Gauss had ontdekt!

En hoe zien die andere negen glijliniaalconstructies uit het boekje eruit? Heel verschillend, maar die cirkel met straal $\sqrt{2}$ zie je wel vaak terug. De negende constructie gebruikt alleen maar cirkels met straal $1.$ Daar hoef je de passer dus niet voor te verstellen. Of de constructies erg praktisch zijn betwijfel ik. Het boekje is vast geschreven door een liefhebber die erg gefascineerd was door de zevenhoek. Maar zo is veel mooie wiskunde ontstaan!

De machtsstelling

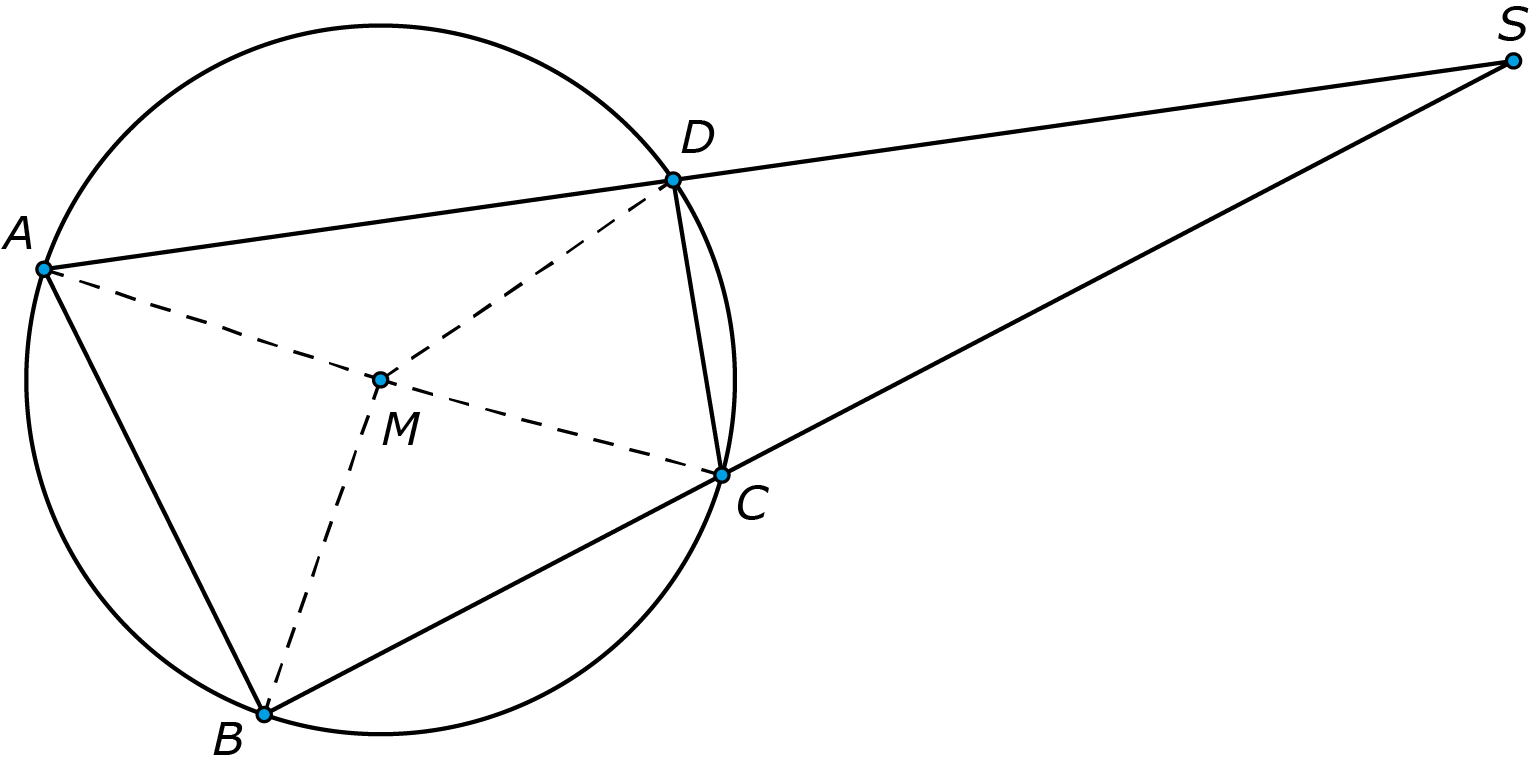
De machtsstelling zegt dat in de figuur geldt: $AS \cdot DS = BS \cdot CS.$ Het bewijs gebruikt de gelijkvormigheid van de driehoeken $ABS$ en $CDS.$ De twee driehoeken hebben hoek $S$ gemeenschappelijk en verder is bijvoorbeeld $\angle SAB = \angle SCD.$ Dat is zo, omdat de vier driehoekjes die in $M$ samenkomen gelijkbenig zijn, waardoor je kan zien dat $\angle DAB + \angle DCB = 180^{\circ}.$ Kijk maar eens goed en probeer.