Een heel oud verhaal laat zien hoe sterk exponentiële groei kan zijn. Het is een verhaal over de oorsprong van het schaakspel. De uitvinder presenteert het spel aan de koning en mocht zelf de prijs noemen die hij als beloning wilde hebben. Hij weigerde alle gebruikelijke voorstellen en wilde iets eenvoudig dat passend was bij zijn bescheiden persoon. Zijn schaakbord bestond uit $64$ vierkantjes en hij wilde $1$ korrel rijst op het eerste vierkant, dan $2$ korrels op het tweede vierkant, $4$ korrels op het derde vierkant en zo verder met iedere keer een verdubbeling van het aantal korrels tot het laatste vierkantje.

Dat lijkt niet zo ingewikkeld. Dit is een voorbeeld van exponentiële groei (of specifieker, een meetkundige rij). Hoeveel rijstkorrels zijn dat? Je kunt de hoopjes op elk veld zien als machten van $2$. Op het eerste vakje liggen $2^0$ korrels, op het tweede vakje $2^1$, op het derde vakje $2^2$ enzovoorts. Je kunt het totale aantal rijstkorrels berekenen met gebruik van de somformule voor meetkundige reeksen. Je kunt ook een meer intuïtief pad inslaan en het totale aantal korrels zien als een binair getal met 64 enen.

	Opgave 1 Probeer één van beide methodes en bereken hoeveel rijstkorrels de uitvinder zou moeten krijgen.

De uitkomst van deze opgave zegt de meeste mensen niet zo veel. Een getal leeft in je hoofd. Wij hebben meer aan een gewicht dat wij kunnen voelen of nog beter een inhoud die wij kunnen zien. Om een beeld te vormen van hoe groot die hoeveelheid rijstkorrels is heb ik de volgende maten en feiten gebruikt.

 

Er zijn ongeveer $42$ rijstkorrels in $1\ {\rm cm}^3$. Zie foto. Een container heeft een inhoud van ongeveer $33{,}1 {\rm m}^3$. Een treinstel met een lengte van ongeveer $19{,}4$ m kan $3$ containers vervoeren. De omtrek van de aarde ter hoogte van de evenaar is $40\ 000$ km. Je rekenmachientje drukt het aantal korrels uit als ongeveer $1{,}84 \times 10^{19} korrels$.

 

	Opgave 2 Hoeveel rijst was dat uitgerekend in treinstellen om de evenaar?  Na de berekening kun je een mening vormen over de vraag of de uitvinder zijn wens heeft gekregen.

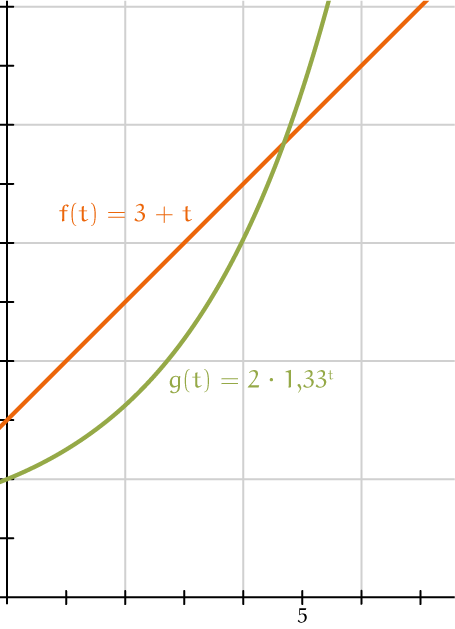
Maar hoe sterk is exponentiële groei in vergelijking met andere soorten groei? We maken nu een sprong in de tijd. In 1798 deed Thomas Malthus een voorspelling. Omdat de bevolking in die tijd exponentieel groeide en de voedselproductie lineair groeide zou het aantal mensen uiteindelijk te groot zijn voor het beschikbare voedsel. Dit idee heeft ook invloed gehad op Darwin. Lineaire groei is te beschrijven als een functie met een formule van de vorm: $f(t) = a + bt$ met de constante $a$ als beginwaarde en de constante $b$ als stapgrootte en $t$ als tijdsvariabele. De grafiek hiervan is een rechte lijn. Exponentiële groei is te beschrijven als een functie met een formule van de vorm: $g(t) = c \cdot d^t$ met de constante $c$ als beginwaarde en de constante $d$ als groeifactor en $t$ weer als tijdsvariabele. De bewering van Malthus was gebaseerd op statistieken uit die tijd. Een sterkere bewering is dat als $c > 0$ en $d > 1$ dan zou elke exponentiële functie uiteindelijk grotere waarden hebben dan elke lineaire functie. Zie de grafiek waar in een concreet geval $g(t)$ groter wordt dan $f(t)$ voor $t \approx 4{,}75$.

	Opgave 3 Maak het bewijs voor deze sterkere bewering. HINT: Laat zien dat boven een bepaalde waarde van $t$ de functie $g(t)$ sneller groeit dan $f(t)$ en dus $f(t)$ uiteindelijk moet inhalen. Vergelijk hiervoor $g(t+1) - g(t)$ met $f(t+1) - f(t)$.

Het geval van Malthus laat zien dat als ze naast elkaar groeien exponentiële groei uiteindelijk sterker is dan lineaire groei. In het volgende voorbeeld groeien ze niet naast elkaar maar in direct conflict met elkaar en is de tijd beperkt.

Hypotheek

De meeste mensen die een huis willen kopen, moeten een lening afsluiten bij een bank. Eén type lening is een annuïteithypotheek. De bank vraagt een rentepercentage (= de groeifactor) dus je schuld groeit exponentieel. Hiertegen moet je een vaste lineaire aflossing doen. Deze twee tendensen vechten tegen elkaar totdat na $30$ jaar de lening afbetaald is. Dit vraagt in elk concreet geval om een berekening van de vaste maandelijkse aflossing. Hierbij wordt na elke maand eerst de rente berekend en dan de aflossing. De rente per maand $r$ wordt bepaald vanuit de jaarrente: $1 + r = (1 + R)^{\frac{1}{12}}$. Er is een begin gemaakt van een tabel met maanden en de hoogte van de schuld na elke maand. Hier gebruik ik de variabelen $P$ voor de omvang van de lening, $R$ voor de jaarlijkse rente en $b$ voor de omvang van de maandelijkse aflossing. De nieuwe schuld na iedere maand wordt gevormd door de oude met een factor $f$ te vermenigvuldigen en de aflossing $b$ van het resultaat af te trekken, waar $f = (1 + R)^{\frac{1}{12}}$. Hierbij ontstaat een patroon en een algemene uitdrukking voor de hoogte van de schuld na elke maand. Aan het eind van $30$ jaar ($360$ maanden) hoort dit nul te zijn en dit geeft een formule voor $b$ in termen van $P$ en $R$.

Maand		Schuld
$0$		$P$
$1$		$Pf-b$
$2$		$(Pf-b)f-b=Pf^2-b(f+1)$

 

	Opgave 4 Maak de formule voor $b$ in termen van $P$ en $R$ en controleer je formule in het geval dat $P = \mbox{€ }200\ 000$ en $R = 6\%$. Als het goed is komt er dan $b = \mbox{€ }1\ 178{,}74$ uit.

 

Dit voorbeeld geeft hoop dat iets zoals het coronavirus, dat exponentieel kan groeien, in te tomen valt. Bovendien kan de groeifactor van het virus veranderen onder invloed van goed gedrag en vaccinaties.

 

Bekijk oplossing