John Conway was een van de origineelste wiskundigen van de laatste 100 jaar. Op 11 april 2020 bezweek hij aan covid-19. Hij werd 82. Conway is vooral bekend als uitvinder van The Game of Life. Hij was actief in verschillende takken van de wiskunde, en verschillende begrippen in de wiskunde zijn naar hem vernoemd.
In 2014 verscheen Conway’s bewijs van de trisectricestelling van Frank Morley, een eigenschap in een driehoek waar Morley in 1899 toevallig op botste.

	Stelling van Morley Gegeven een willekeurige driehoek. Vanuit elk hoekpunt vertrekken er $2$ rechten die die hoek in $3$ gelijke delen verdelen, de trisectrices. Per paar hoekpunten bepalen we het snijpunt van de $2$ trisectrices die het dichtst bij de zijde liggen die die $2$ hoekpunten verbindt. Deze $3$ snijpunten vormen een gelijkzijdige driehoek, de driehoek van Morley.

Figuur 1 laat zien wat de stelling precies inhoudt. We starten met een willekeurige driehoek.

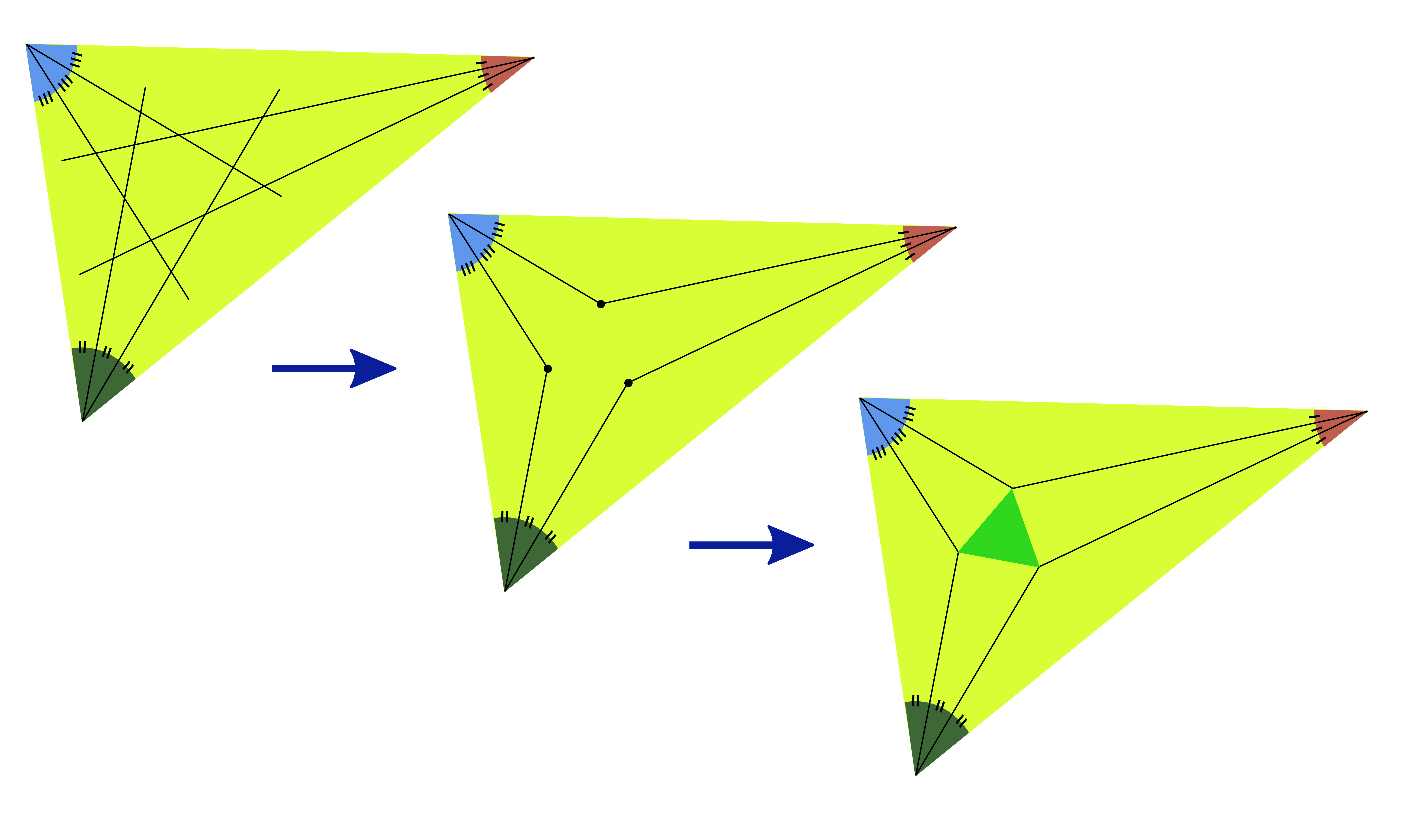
We verdelen elk van de drie hoeken in drie gelijke delen. We tekenen dan de $6$ rechten op de figuur, en bepalen de $3$ snijpunten die je aangeduid ziet op de figuur. Deze drie punten vormen steeds een gelijkzijdige driehoek, welke vorm de driehoek waarmee je start ook heeft.
Deze eigenschap stond bekend als zeer moeilijk om te bewijzen. We laten zien hoe Conway het deed. Voor het bewijs gebruiken we wat elementaire meetkunde maar niet veel meer dan dat. Onder andere de eigenschap dat de som van de hoeken van een driehoek gelijk is aan $180^{\rm o}$. We vertrekken van een willekeurige driehoek zoals in figuur 1, noem de hoeken $\alpha$, $\beta$ en $\gamma$. We verdelen elke hoek in drie gelijke delen, en we werken nu verder met de hoeken $\frac{\alpha}{3}$ , $\frac{\beta}{3}$ en $\frac{\gamma}{3}$ . Elk van deze hoeken stellen we voor  met een kleur, de som ervan is dus $60^{\rm o}$ wat te zien is op de figuur 2 links. We nemen verder ook een gelijkzijdige driehoek (figuur 2 rechts).

Nu plaatsen we op de drie zijden van deze gelijkzijdige driehoek even grote gelijkzijdige driehoeken (figuur 3a links - de grijze driehoeken):

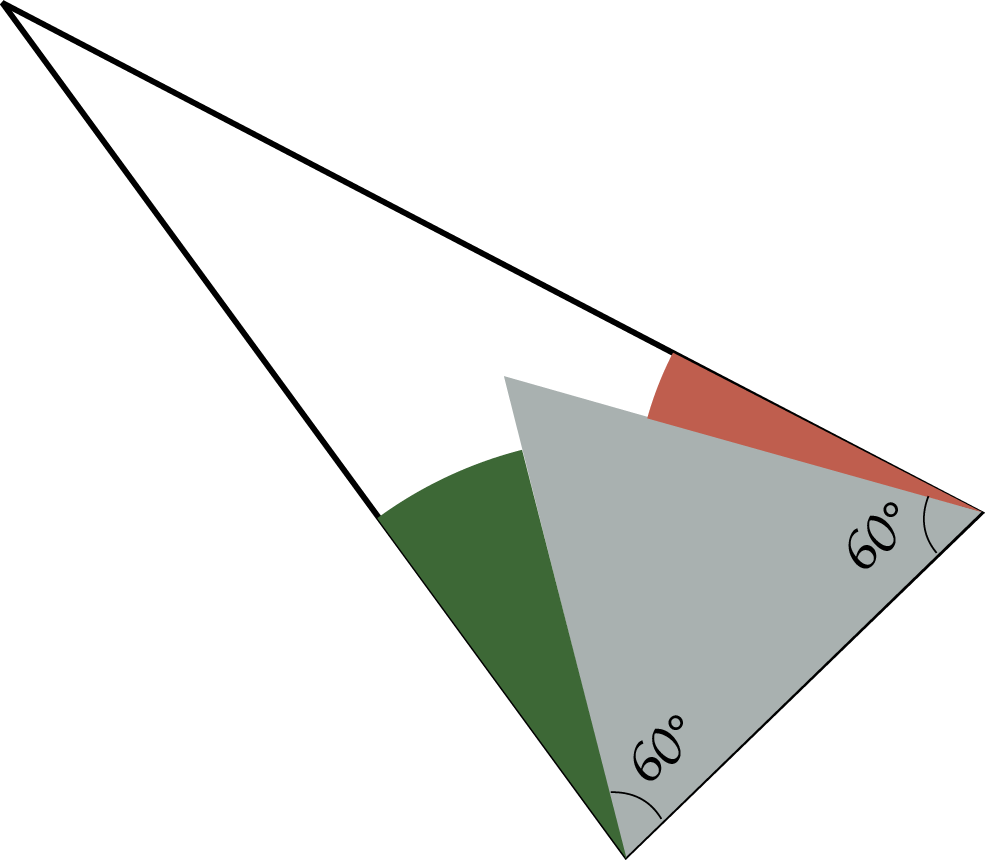
en we passen dan vanuit de hoekpunten van de gegeven gelijkzijdige driehoek de drie gekleurde hoeken af zoals in figuur 3a (rechts), Door lijnen te verlengen krijgen we dan drie nieuwe driehoeken. Linksboven bijvoorbeeld krijgen we dan de driehoek op figuur 3b. Van deze driehoek kennen we twee hoeken, namelijk groen + grijs en bruin + grijs. Maar grijs = $60^{\rm o}$. En de som: (groen + grijs) + (bruin + grijs) + (nieuwe hoek) moet $180^{\rm o}$ geven. Dat kan alleen indien de derde hoek gelijk is aan de blauwe hoek, want groen + bruin + blauw = $60^{\rm o}$. Ook van de andere twee nieuwe driehoeken in figuur 4 kennen we zo de derde hoek:

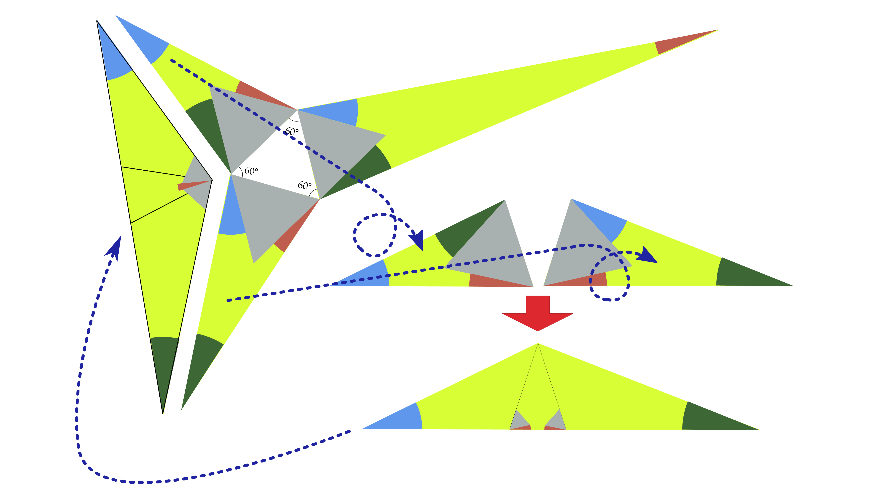
In een volgende stap halen we de nieuwe driehoeken linksboven en linksonder even uit de figuur, spiegelen ze om een van de zijden, en leggen ze naast elkaar zoals in figuur 5:

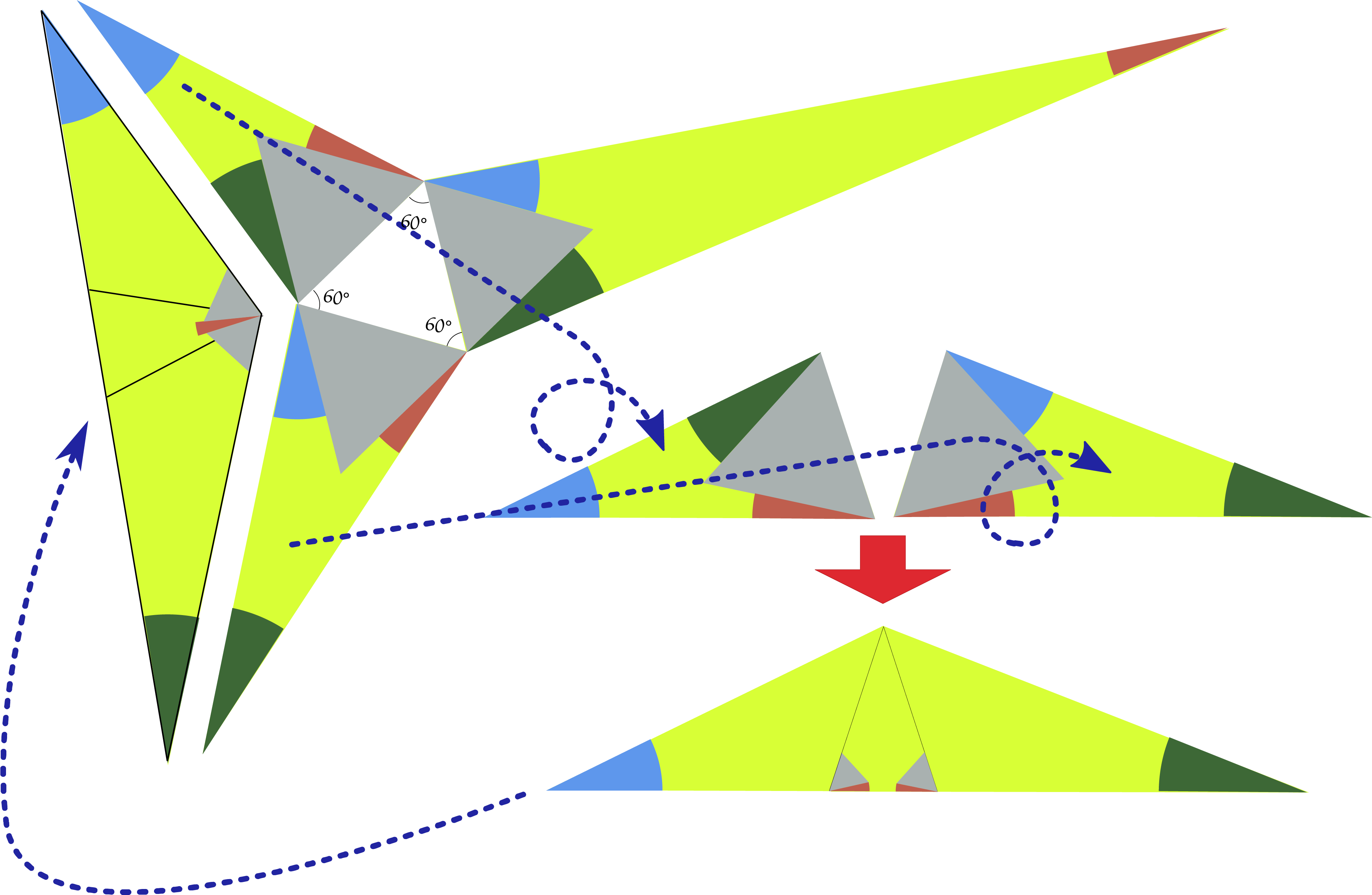
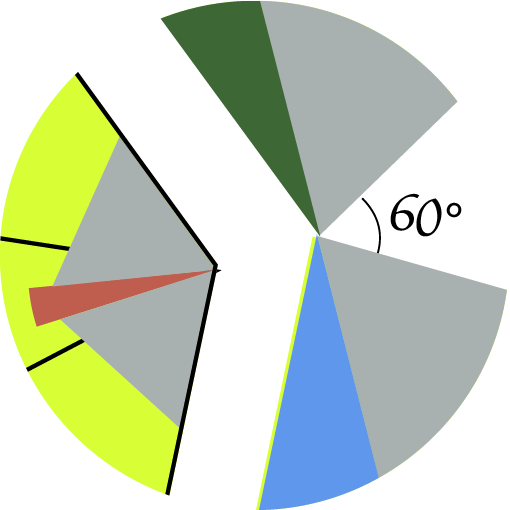
Uit symmetrie-overwegingen volgt dadelijk dat deze twee driehoeken dezelfde hoogte hebben, en we kunnen ze dan ook over elkaar schuiven zoals onderaan te zien is. Merk op dat de tophoek van deze nieuwe driehoek gelijk zal zijn aan grijs + bruin + grijs, want de drie hoeken geven samengeteld natuurlijk weer $180^{\rm o}$ (en we hebben al blauw + groen). Je ziet dit links op de figuur 5 (volg de pijl). Het resultaat proberen we nu in te passen in de figuur die we al hadden. Merk op dat de zijden die tegen elkaar moeten komen dezelfde lengte hebben (een gevolg van het spiegelen), maar de vraag is: past ook de hoek in het gat? We kunnen uitrekenen hoe groot het gat is, zie figuur 6, een detail van de vorige figuur:

Samen met de hoeken groen + grijs + wit + grijs + blauw moeten we aan 360° komen, en wit = grijs = 60°. We hebben dus nog 120° + bruin tekort, of nog: grijs + bruin + grijs. Dus het past!
Precies dezelfde redenering laat ons toe de twee andere gaten in de figuur op te vullen (figuur 7):

 

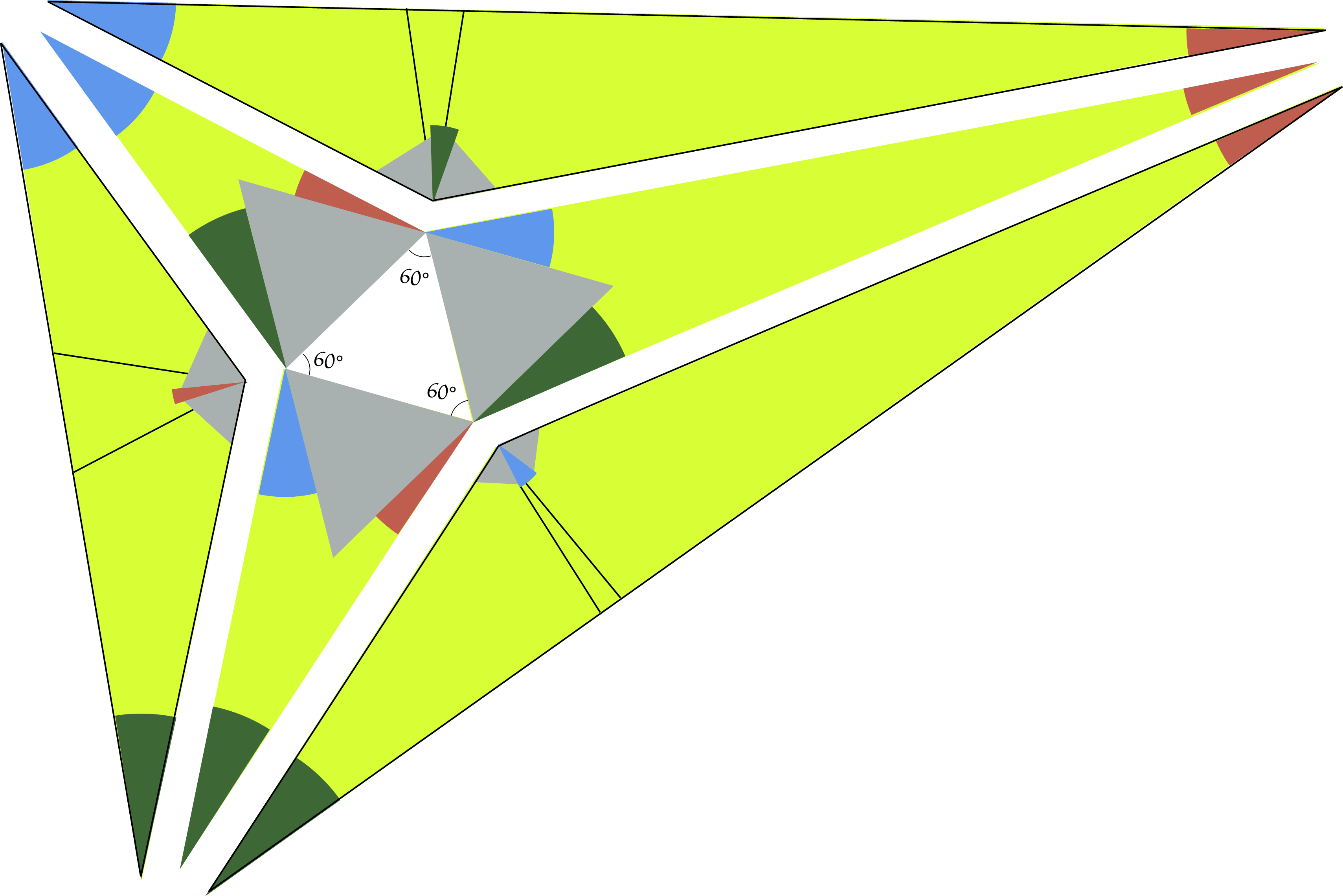
	Dit leidt uiteindelijk tot: 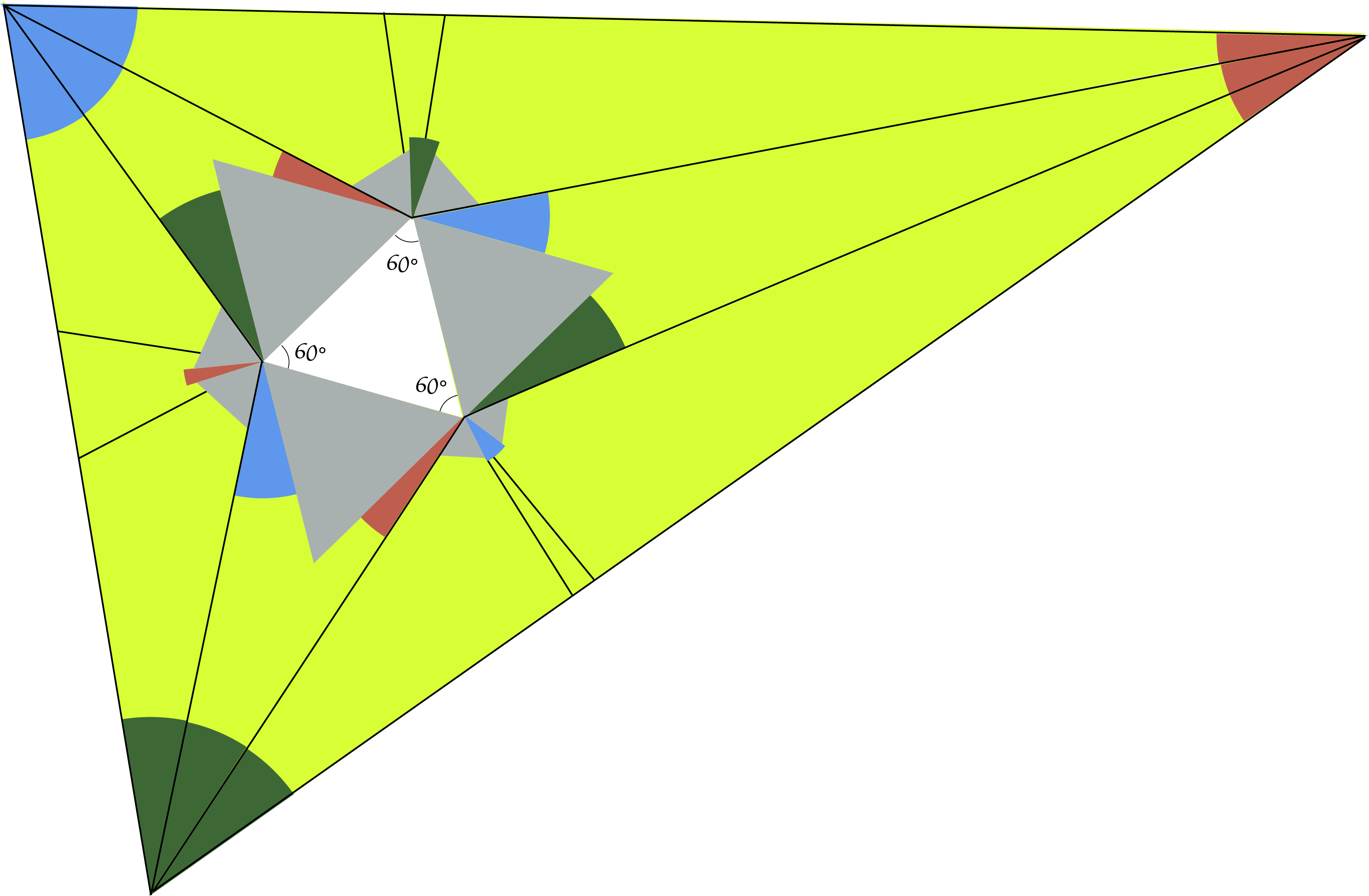En hiermee is de stelling bewezen: in figuur 8 zie je de willekeurige driehoek waarmee we gestart zijn en waarvan de hoeken in $3$ gelijke delen verdeeld zijn.