
De Trisectricestelling van Morley
Als je in een driehoek de drie hoeken in drieën deelt en de snijpunten van de twee aanliggende trisectrices uit twee verschillende hoeken neemt dan vormen de drie snijpunten een gelijkzijdige driehoek.
De stelling van Morley, uit 1904, zegt iets over de trisectrices van een driehoek. Als je in een driehoek de drie hoeken in drieëen deelt en de snijpunten van trisectrices neemt zoals in het plaatje aangegeven, dan vormen de drie snijpunten een gelijkzijdige driehoek.
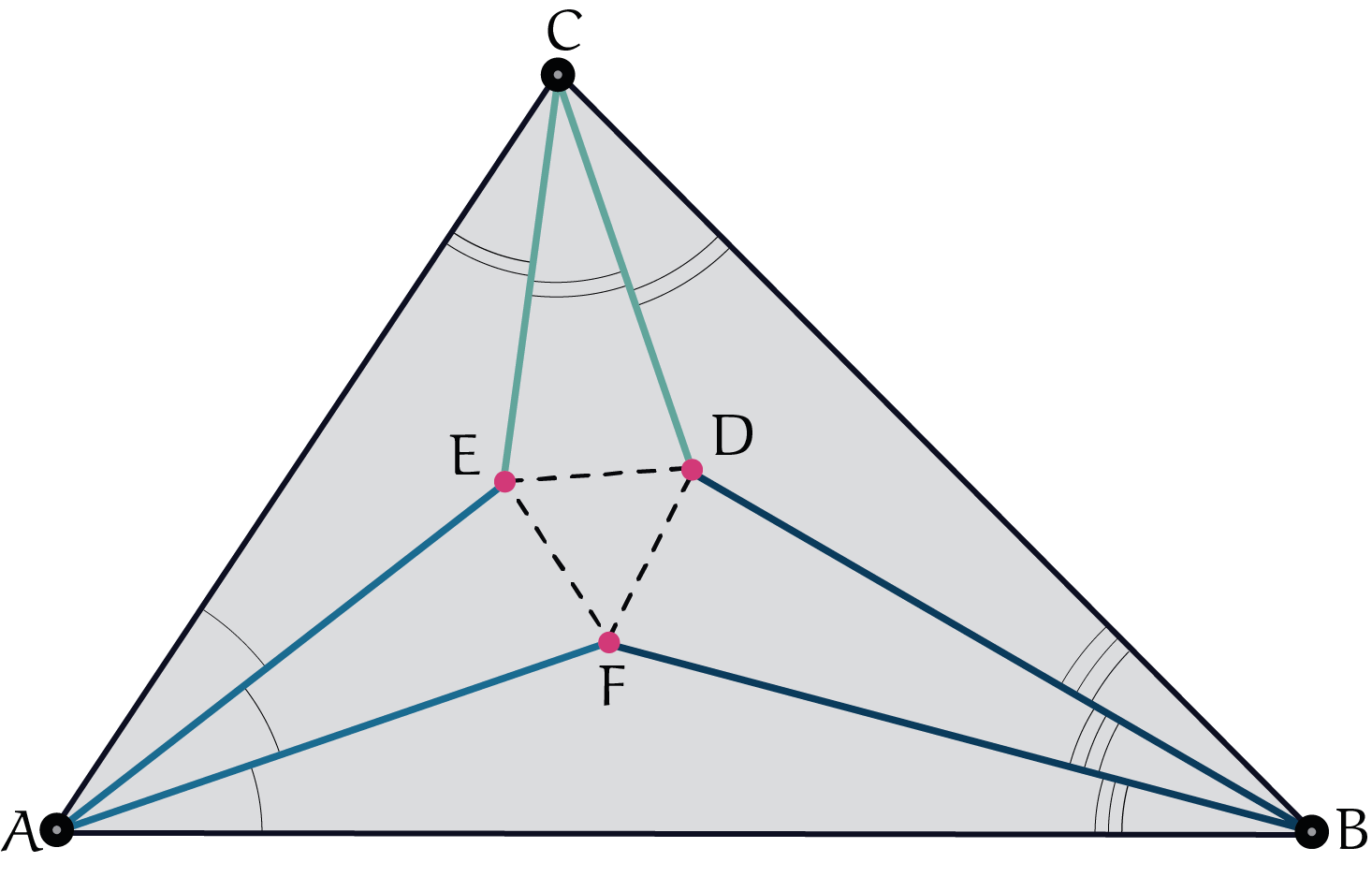
Er zijn veel bewijzen van deze stelling bedacht. Zo kun je bijvoorbeeld met behulp van de sinusregel de zijden van de kleine driehoek in de sinussen van de oorspronkelijke hoeken uitdrukken, met wat werk kun je afleiden dat
$$EF=8R\sin\frac{1}{3}A \sin\frac{1}{3}B \sin\frac{1}{3}C.$$
Hierin is $R$ de straal van de omgeschreven cirkel van driehoek $ABC$.
De vorm van de formule laat zien dat je hetzelfde zult krijgen voor $FD$ en $DE$.
Een ander bewijs werkt achteruit: het begint met driehoek $DEF$ en reconstrueert dan een driehoek die gelijkvormig is met de gegeven driehoek $ABC$.

Je kunt het nog eens nalezen in Hoofdstuk X van het boek Hoofdstukken uit de Elementaire Meetkunde van O. Bottema (Epsilonreeks, nummer 9)
| Feuerbach | Poncelet | Pascal | Morley | Torricelli | Ceva |
