Licht werk met goed algoritme
[oOO]
Als eerstejaarsstudent Wiskunde aan de Universiteit Utrecht hebben we voor het vak Programmeren voor de Wiskunde als eindproject in een groepje een algoritme gemaakt dat een Light-up puzzel kan oplossen. Light-up is een logische puzzel, vergelijkbaar met Sudoku. In deze driedelige serie gaan we het hebben over de Light-up puzzel en ons algoritme. In dit eerste artikel kijken we naar de regels en basisstrategieën. In het tweede artikel kijken we naar geavanceerdere strategieën, en in het laatste artikel kijken we hoe we een computer deze puzzel kunnen laten oplossen.
|
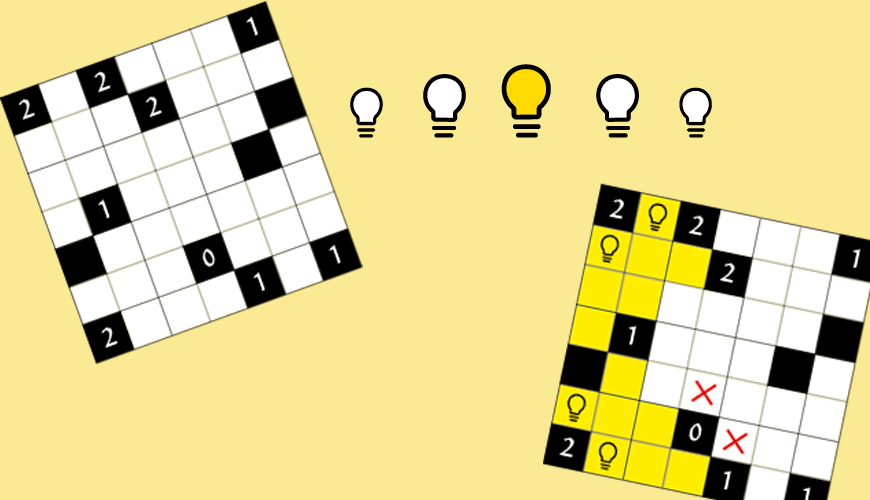
Light up wordt op een rechthoekig bord gespeeld. Het bord heeft witte en zwarte vakjes. Het doel is om lampjes te plaatsen op een aantal witte velden zodat elk wit veld verlicht wordt. Een vakje wordt belicht door een lampje als ze in dezelfde rij/kolom staan, en er geen zwarte velden tussen zitten. Het is verboden voor twee lampjes om elkaar te beschijnen. Een aantal zwarte velden bevat een getal, dat aangeeft hoeveel lampjes er in de omringende 4 velden staan (dus niet schuin). Zo'n vakje met een getal noemen we een hint. In figuur 1 staat een voorbeeld van een Light-up puzzel in de beginsituatie, met in figuur 7 de oplossing. Light-up puzzels zijn altijd zo gemaakt dat er een unieke oplossing is, die gevonden kan worden door logische deductie zonder te gokken. Om een Light-up puzzel op te lossen hoef je alleen maar aan te geven in welke vakjes de lampjes komen, maar tijdens het oplossen helpt het om een vakje te markeren als je zeker weet dat dat vakje geen lampje bevat. Er kan in dat geval een kruisje in dat vakje worden geplaatst. Er is een aantal eenvoudige deducties, waarmee je simpele Light-up puzzels kan oplossen. Het eerste waar je naar kijkt zijn de hints. Om een 0-hint kan je kruisjes zetten. Dit kan zelfs nog iets algemener. Als er bijvoorbeeld al een lampje staat om een 1-hint, dan kan je kruisjes zetten in de andere vakjes om die hint. In het algemeen is dit als volgt te formuleren: als het aantal lampjes om een hint gelijk is aan de hint, dan kan je kruisjes in de andere omringende vakjes zetten. Deze redenering kunnen we ook omkeren. Als het aantal lege vakjes om een hint gelijk is aan het aantal lampjes dat de hint nog nodig heeft, dan kunnen we een lampje op al die lege vakjes plaatsen. Een vakje noemen we leeg als hij wit is en nog geen kruisje of lampje bevat. Een soortgelijke logica kunnen we ook toepassen op segmenten. Een segment is een deel van een rij/kolom tussen twee zwarte vakjes, of tussen een zwart vakje en de rand. Als we een lampje plaatsen, dan kunnen we kruisjes zetten in alle vakjes in die in hetzelfde horizontale segment zitten als het vakje waar we een lampje hebben geplaatst, en idem voor het verticale segment. De omkering van deze redenering is iets ingewikkelder. Als het horizontale segment en het verticale segment van een nog niet belicht vakje samen nog maar één leeg vakje bevatten, dan kunnen we een lampje plaatsen op dit vakje. De reden hiervoor is dat het eerstgenoemde vakje anders niet belicht zou worden. Door deze deducties herhaaldelijk toe te passen, kunnen we de voorbeeldpuzzel van hierboven oplossen. We kunnen eerst kruisjes en lampjes om een aantal hints heen zetten (figuur 2). Een geel vakje betekent dat het vakje al belicht wordt. Omdat het hierdoor al visueel duidelijk is dat er geen lampje meer op mag, zetten we geen kruisje op gele vakjes. Omdat we nu van een aantal vakjes weten dat er geen lampje op staat, zijn er nieuwe hints waar we lampjes omheen kunnen zetten, namelijk de rechter 2 in de bovenste rij, de linker 1 in de onderste rij en de 1 in de middelste rij (figuur 3). We kunnen nu een lampje zetten onder de 1 die rechtsboven staat (figuur 4). In figuur 5 hebben we nu ook de laatste 2 ingevuld. Omdat we nu alle hints gebruikt hebben, moeten we overgaan op de segmenten. Het linker vakje met een kruisje ziet nog maar één leeg veld, dus daar zetten we in figuur 6 een lampje. Met dezelfde logica kunnen we nu ook het laatste lampje invullen. In figuur 7 staat de oplossing. Deze elementaire afleidingen zijn dus al voldoende om een eenvoudigere Light-up puzzel op te lossen. Maar voor moeilijkere puzzels zijn er ook ingewikkeldere afleidingen nodig. In het volgende artikel gaan we die in meer detail behandelen, maar we gaan nu ook al kijken naar een iets minder elementaire deductie. Bekijk de situatie in deel figuur 8. Het is niet mogelijk om een lampje in de hoek linksboven neer te zetten, want dan kan de 3 nog maar hooguit 2 lampjes krijgen. We kunnen dus een kruisje in die hoek zetten, en hetzelfde geldt voor de andere hoeken. Deze redenering kunnen we ook toepassen bij een 2 hint met nog maar drie vrije vakjes, of een 1 hint met twee vrije vakjes die een hoekpunt gemeen hebben. In de voorbeeldpuzzel hadden we dus ook al meteen een kruisje kunnen zetten in het vakje links onder de 1 rechtsboven.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

 1
1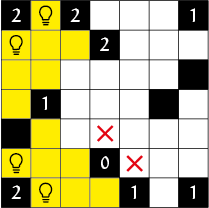 2
2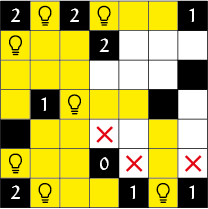 3
3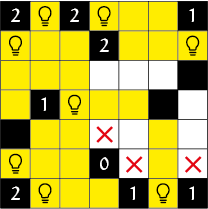 4
4 5
5 6
6 7
7 8
8