In het bovengenoemde artikel deed zich nog een probleem voor: sommige rekenmachines, en websites als Wolfram Alpha, kwamen voor machten als $(-1)^{1{,}2}$ en $(-1)^{1{,}3}$ op andere antwoorden uit dan de $\pm 1$ die de algebra ons gaf.

Met behulp van de formules van Caspar Wessel uit Pythagoras 63-5 kunnen we een definitie van $(-1)^x$ geven voor alle reële getallen $x$ en wel zo dat aan alle rekenregels is voldaan. En je raadt het al: we gaan dus complexe getallen gebruiken.

De oplossing gebruikt de volgende formule uit het artikel over Caspar Wessel:

$$(\cos(v) + \varepsilon \sin(v))(\cos(u) + \varepsilon \sin(u)) = \cos(v + u) + \varepsilon sin(v + u).$$

Als je $f(v) = \cos(v) + \varepsilon \sin(v)$ schrijft dan staat daar $f(v) \cdot f(u) = f(v + u)$, en dat is precies wat je van een exponentiële functie verwacht.

Verder hadden we gezien dat $\varepsilon^2 = -1$, voor Wessel was dat reden genoeg om $\varepsilon=\sqrt{-1}$ te schrijven. En wij schrijven daarom $(-1)^{\frac{1}{2}}=\varepsilon$. Dan volgt dat $\varepsilon$ gelijk moet zijn aan $-1\cdot(-1)^{\frac{1}{2}}=(-1)^{\tfrac{1}{2}}$.

Wat zou $(-1)^{\tfrac{1}{4}}$ moeten zijn? De formule van Wessel laat zien dat kwadrateren neerkomt op hoeken verdubbelen:

$\left(\cos(v) + \varepsilon \sin(v)\right)^2 = cos(2v) + \varepsilon sin(2v)$.

Nu hebben we $\varepsilon = \cos\left(\frac{\pi}{2}\right) + \varepsilon \sin\left(\frac{\pi}{2}\right) $, en $\varepsilon$ zou het kwadraat van $(-1)^{\frac{1}{4}}$- moeten zijn, dus een voor de hand liggende keuze is de hoek van $\varepsilon$ halveren

$$(-1)^{\frac{1}{4}}=\cos\left(\frac{\pi}{4}\right) +\varepsilon\sin\left(\frac{\pi}{4}\right) = \tfrac{1}{2}\sqrt{2}+\varepsilon\cdot\tfrac{1}{2}\sqrt{2}.$$

Maar dan kunnen we ook $(-1)^{\frac{3}{4}}$, $(-1)^\frac{5}{4}$ en $(-1)^{\frac{7}{4}}$ vastleggen door de optelregel te gebruiken, zie figuur 1.

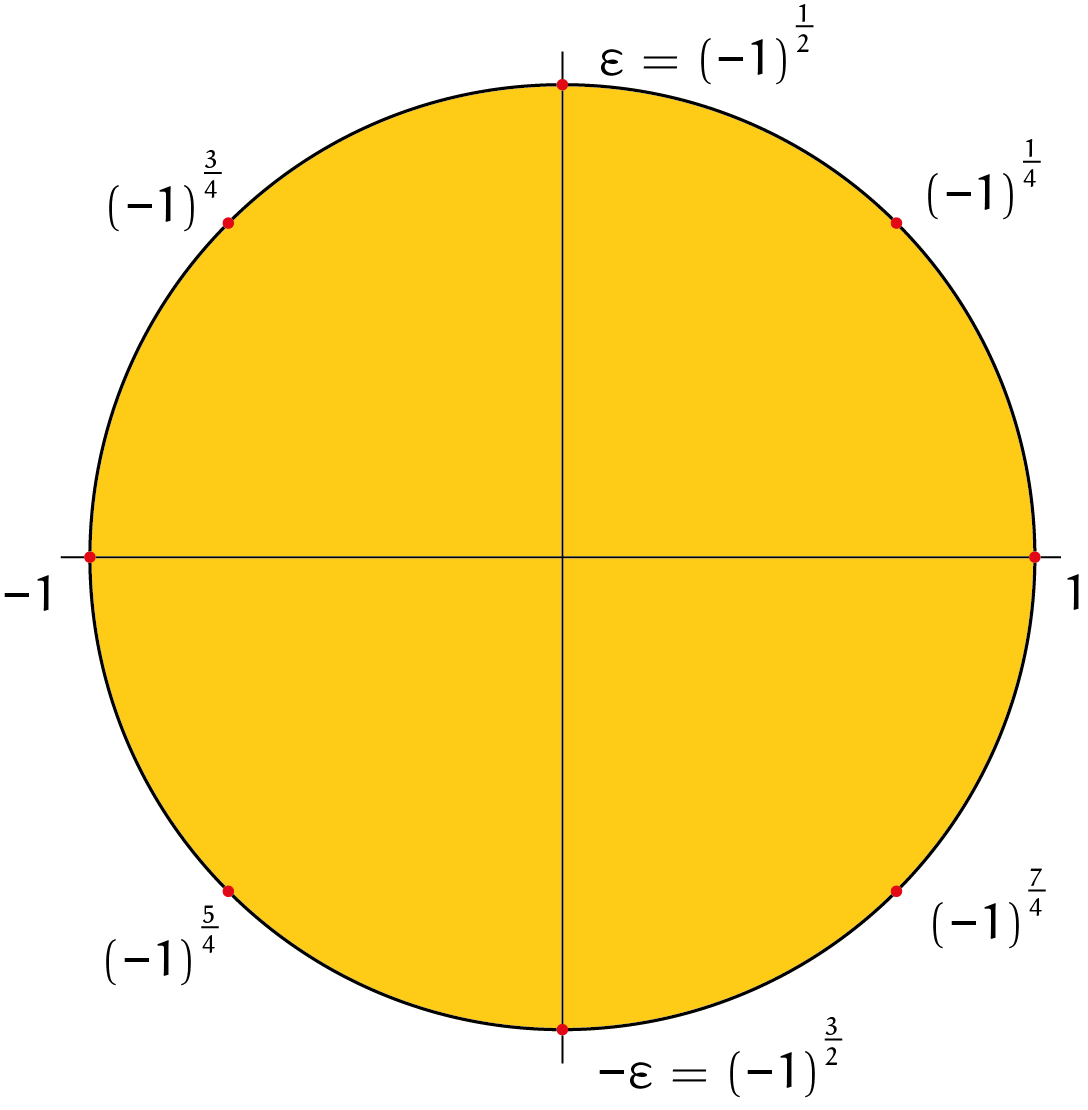
In al onze voorbeelden hebben we eigenlijk de exponent met $\pi$ vermenigvuldigd en daarna de cosinus en sinus genomen. Dat wordt onze algemene definitie:

$$(-1)^x = \cos(\pi x) + \varepsilon \sin(\pi x).$$

Deze functie voldoet dus aan de optelregel voor exponenten en is netjes continu, want de sinus en de cosinus zijn continu. Precies wat je in de wiskunde wilt hebben.

Rare(?) verschijnselen

De exponentiële functie die we nu gemaakt hebben gedraagt zich wel wat anders dan we gewend zijn: hij is namelijk periodiek, omdat de cosinus en sinus dat zijn; er geldt $(-1)^{x+2} = (-1)^x$ , dus de periode is gelijk aan $2$.

Verder krijgen we voor oneven $q$ andere waarden voor $(-1)^{\frac{1}{q}}$ dan uit de algebraïsche overwegingen, niet meer $-1$ maar $\cos\left(\frac{\pi}{q}\right) + \varepsilon \sin\left(\frac{\pi}{q}\right)$. Maar die formule werkt nu voor alle $q$ en zo krijgen we dus bijvoorbeeld ook de waarden voor $(-1)^{\frac{1}{2}}$ en $(-1)^{\frac{1}{4}}$ die we al gekozen hadden: 

$(-1)^{\frac{1}{2}}=\varepsilon$ en $(-1)^{\frac{1}{4}}=\tfrac{1}{2}\sqrt{2}+\tfrac{\varepsilon}{2}\sqrt{2}$ (want $\cos\left(\frac{\pi}{4}\right)=\sin\left(\frac{\pi}{4}\right)=\tfrac{1}{2}\sqrt{2}$).

De rekenmachines waar we het in het begin over hadden gebruiken deze definitie ook. De waarden die we in het vorige artikel gezien hebben, namelijk

$$(-1)^{1{,}2}=-0{,}809017\dots - 0{,}587785\dots i$$

en

$$(-1)^{1{,}3}=-0{,}587785\dots -0,809017\dots i.$$

volgen meteen uit onze definitie; kijk maar wat de cosinussen en sinussen van $1{,}2\pi$ en $1{,}3\pi$ zijn. Kun je de symmetrie in de antwoorden meetkundig verklaren? (Kijk waar die punten op de eenheidscirkel liggen.) Niet alleen krijgen we andere waarden voor $(-1)^{\frac{1}{q}}$, we hebben ook meer oplossingen voor $z^q = -1$.

Dat komt door de periodiciteit van $(-1)^x$. Neem $z_0 = (-1)^{\frac{1}{q}}=\cos\left(\frac{\pi}{q}\right)+\varepsilon\sin\left(\frac{\pi}{q}\right)$. Dan geldt $z_0^q = -1$. We maken nog een oplossing door de periode te gebruiken: neem $x_1=\frac{1}{q}+\frac{2}{q}$ en

$$z_1=(-1)^{x_1} = \cos\left(\frac{3\pi}{q}\right)+\varepsilon\sin\left(\frac{3\pi}{q}\right).$$

Dan geldt $z_1^q =(-1)^{q\cdot x_1}=(-1)^{1+2}=(-1)^1=-1$.

Zo kun je doorgaan: $x_2=\frac{1}{q}+\frac{4}{q}$ en

$$z_2=(-1)^{x_2}=\cos\left(\frac{5\pi}{q}\right)+\varepsilon\sin\left(\frac{5\pi}{q}\right).$$

Maar dit stopt bij  $x_{q-1}=\frac{1}{q}+\frac{2(q-1)}{q}$ en $z_{q-1}=(-1)^{x_{q-1}}$. Immers de volgende stap, met $x_q=\frac{1}{q}+\frac{2q}{q} $ levert nu

$z_q=(-1)^{x_q}=(-1)^{\frac{1}{q}+2}=(-1)^{\frac{1}{q}}=z_0$.

We zien dat $z^q = -1$ precies $q$ oplossingen heeft en als je ze tekent krijg je een mooie regelmatige $q$-hoek. Figuur 2 toont het plaatje bij $q = 5$.

 

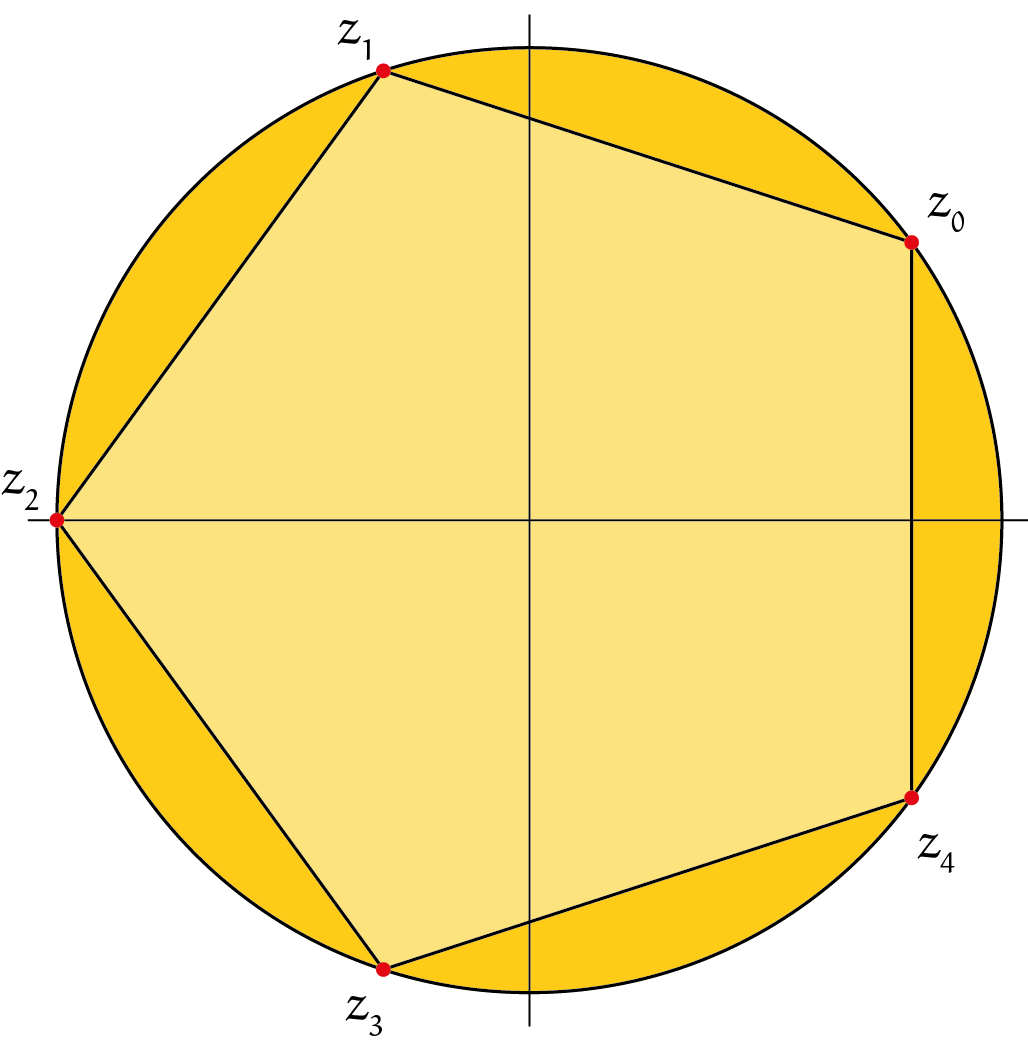
Opgave 1 Bereken zelf $(-1)^{\frac{1}{q}}$ voor $q = 3$, $q = 4$ en $q = 6$.

 

Opgave 2 Probeer op dezelfde manier oplossingen van $z^q=1$ te maken, en teken ze voor $q=3$, $q=4$, $q=5$ en $q=6$.

Hier zie je dat de meetkundige vermenigvuldiging van Wessel beter werkt dan de algebraïsche. Als je van een lijnstuk $a + \varepsilon b$ de lengte en richtingshoek weet kun je op deze manier heel snel alle oplossingen van $z^q = a + \varepsilon b$ beschrijven. En dat is wat Caspar Wessel aan het eind van zijn artikel ook deed. Hij liet zien dat er altijd $q$ oplossingen zijn en dat die samen een mooie regelmatige $q$-hoek vormen.

Opgave 3 Probeer zelf maar eens alle oplossingen van $z^q=a+\varepsilon b$ te maken. Doe het eerst uitgaande van de lengte $A$, en de richtingshoek $v$. Bekijk dan hoe je $A$ en $v$ in $a$ ben $b$ kunt uitdrukken.