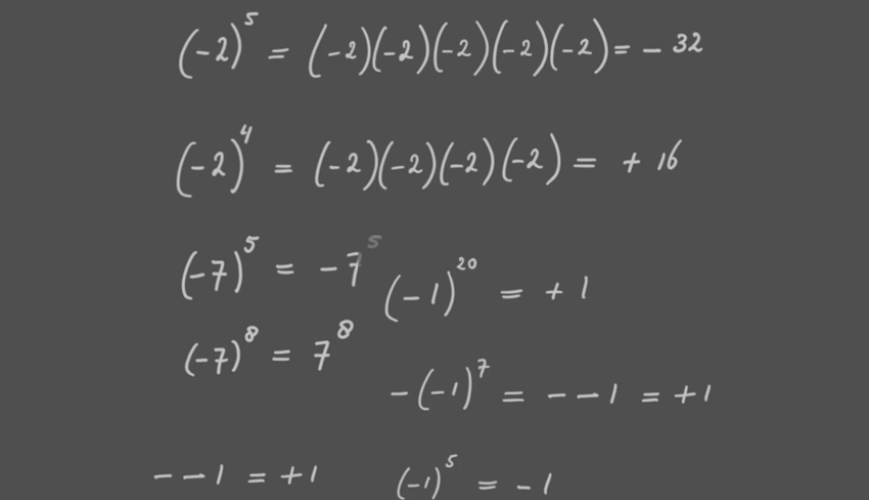
Machten van negatieve getallen
[ooO]
We onderzoeken wat we kunnen zeggen over de functie $a^x$ als $a$ een negatief getal is. We kijken hierbij voornamelijk naar $(-1)^x$.
Als je rekent met machten gebruik je heel vaak de optel- en vermenigvuldigingseigenschappen in de exponenten:
$a^{x+y} = a^x \cdot a^y$ en $a^{x\cdot y} = (a^x)^y$
en daarnaast hebben we ook nog $(ab)^x = a^x \cdot b^x$.
Met behulp van deze formules kun je uitdrukkingen vaak wat overzichtelijker maken en eventueel in een rekenmachientje stoppen om de waarde te bepalen.
Als de $x$ in de exponent een natuurlijk of zelfs een geheel getal is weten we hoe $a^x$ afgesproken is: als $x > 0$ een product van $x$ factoren $a$; als $x = 0$ stellen we $a^x = 1$ en voor negatieve $x$ nemen we $a^x = 1/a^{-x}$. Hiermee zorgen we ervoor dat de bovengenoemde eigenschappen altijd geldig zijn.
Het maakt hier niet uit of $a$ positief of negatief is: $(-2)^x$ heeft voor elk geheel getal $x$ betekenis; wel opletten dat de uitkomst positief is voor even $x$-en en negatief als $x$ oneven is.
Maar als je in je wiskundeboek naar exponentiële functies kijkt, waarbij we $a^x$ voor alle reële getallen bekijken is $a$ altijd positief. In de 45ste jaargang van Pythagoras staat een serie artikelen waarin voor $a = 2$ helemaal wordt uitgelegd hoe je $2^x$ voor alle reële getallen definieert, en hoe je daarmee $a^x$ voor alle positieve $a$ kunt afspreken. Waarom gebeurde dat niet voor negatieve $a$? Dat gaan we hier bekijken.
Rationale exponenten
Een niet-gehele exponent kan een rationaal getal zijn, of een niet-rationaal (maar wel reëel) getal. Een rationaal getal $x$ is altijd te schrijven als een breuk van gehele getallen: $x = p/q$. Het gaat ons om de getallen, we vereenvoudigen daarom de breuken zoveel mogelijk, dus $4/10$ wordt geschreven als $2/5$; $14/4$ als $7/2$, enzovoort. Daarom zijn $p$ en $q$ niet allebei even.
Een niet-rationaal getal is niet als zo'n breuk te schrijven. Daardoor heeft zo'n getal in de decimale schrijfwijze een oneindig aantal decimalen die geen regelmatig patroon vertonen (een rationaal getal kan ook oneindig veel decimalen hebben, maar die herhalen zich telkens, bijvoorbeeld: $3/7 = 0{,}428571\, 428571\ldots$.
In dit artikel gaan we niet proberen om niet-rationale machten van negatieve getallen te berekenen; daar komen complexe getallen bij kijken en daar zullen we het in een later artikel over gaan hebben.
Om te beginnen: we willen de regel $(ab)^x = a^x \cdot b^x$ behouden, dus willen we als $a$ positief is in ieder geval $(-a)^x$ gelijk hebben aan $(-1)^x \cdot a^x$.
Omdat we $a^x$ al kennen hoeven we dus alleen nog naar $(-1)^x$ te kijken. We bekijken dus de machten van $-1$ met rationale exponenten.
We willen de regel $(a^x)^y = a^x\cdot y$ behouden en dat betekent dat we deze gelijkheden willen hebben:
$(-1)^{\frac{p}{q}}=(-1)^{\frac{1}{q}\cdot p}=\left((-1)^{\frac{1}{q}}\right)^p$.
De exponent $p$ is een positief geheel getal, dus die machtsverheffing zal geen probleem zijn, mits we maar weten wat $(-1)^{\frac{1}{q}}$ is.
Maar als we de opteleigenschap $a^{x+y} = a^x \cdot a^y$ ook willen behouden komt $(-1)^{\frac{1}{q}}$ ook vast te liggen.
Immers
$a=a^1=a^{\frac{1}{q}+\cdots+\frac{1}{q}}=a^{\frac{1}{q}}\cdot \cdots \cdot a^{\frac{1}{q}}$
(met $q$ termen $1/q$ in de exponent, en $q$ factoren $a^{\frac{1}{q}}$ aan het eind). Als $a$ positief is is het antwoord duidelijk: $a^{\frac{1}{q}}$ moet gelijk zijn aan de $q$-demachtswortel van $a$. We moeten dus weten wat de $q$-demachtswortel van $-1$ is om de definitie volledig te maken. Vul in de vergelijking hierboven $-1$ in voor $a$:
$-1=(-1)^1=(-1)^{\frac{1}{q}+\cdots+\frac{1}{q}}=(-1)^{\frac{1}{q}}\cdot \cdots \cdot(-1)^{\frac{1}{q}}$.
Het is duidelijk dat de vergelijking voor oneven $q$ klopt als we invullen $(-1)^{\frac{1}{q}}=-1$. Want een oneven aantal factoren $-1$ levert weer $-1$ op.
Maar wat als $q$ even is? Dan hebben we een probleem: we moeten dan voor $(-1)^{\frac{1}{q}}$ een reëel getal invullen en dat een even aantal maal met zichzelf vermenigvuldigen. Dat kan nooit $-1$ opleveren.
Samengevat betekent dit dat $(-1)^{\frac{p}{q}}$ alleen een reëel getal als uitkomst krijgt als $q$ oneven is.
Daarna hangt het van $p$ af: als $p$ even is, is $(-1)^{\frac{p}{q}}=1$, als $p$ oneven is, is $(-1)^{\frac{p}{q}}=-1$.
Als je in een rekenmachientje $(-1)^{1{,}2}$ en $(-1)^{1{,}3}$ intikt krijg je waarschijnlijk een foutmelding maar dat hoeft niet. We schrijven $1{,}2$ en $1{,}3$ als breuken $12/10$ en $13/10$. De eerste kunnen we nog vereenvoudigen tot $6/5$, de tweede niet meer. We kunnen $(-1)^{1{,}2}$ dus toch nog bepalen:
$(-1)^{1{,}2} = \left((-1)^{\frac{1}{5}}\right)^6=(-1)^6=1$
maar bij $(-1)^{1{,}3}$ lukt het niet.
Samengevat: we kunnen $a^b$ zinvol definiëren
- voor alle positieve $a$ en alle $b$;
- voor alle negatieve $a$, mits $b$ te schrijven is als een breuk $b = p/q$ met $q$ oneven.
De uitkomst is positief als $p$ even is, negatief als $p$ oneven is.
Grafieken tekenen
Nu we voor rationale exponenten $b$ weten hoe we om moeten gaan met $(-a)^b$, kunnen we proberen om de grafiek te tekenen van $f(x) = (-a)^x$. Omdat we de functie $e^x$ goed kennen, kiezen we als grondtal $a = e$. De vraag is dus: hoe zou de grafiek van $(-e)^x$ eruit zien?
Hieronder staat een plaatje, dat is gemaakt door $(-e)^x$ voor een zeer groot aantal rationale waarden van $x$ uit te rekenen.
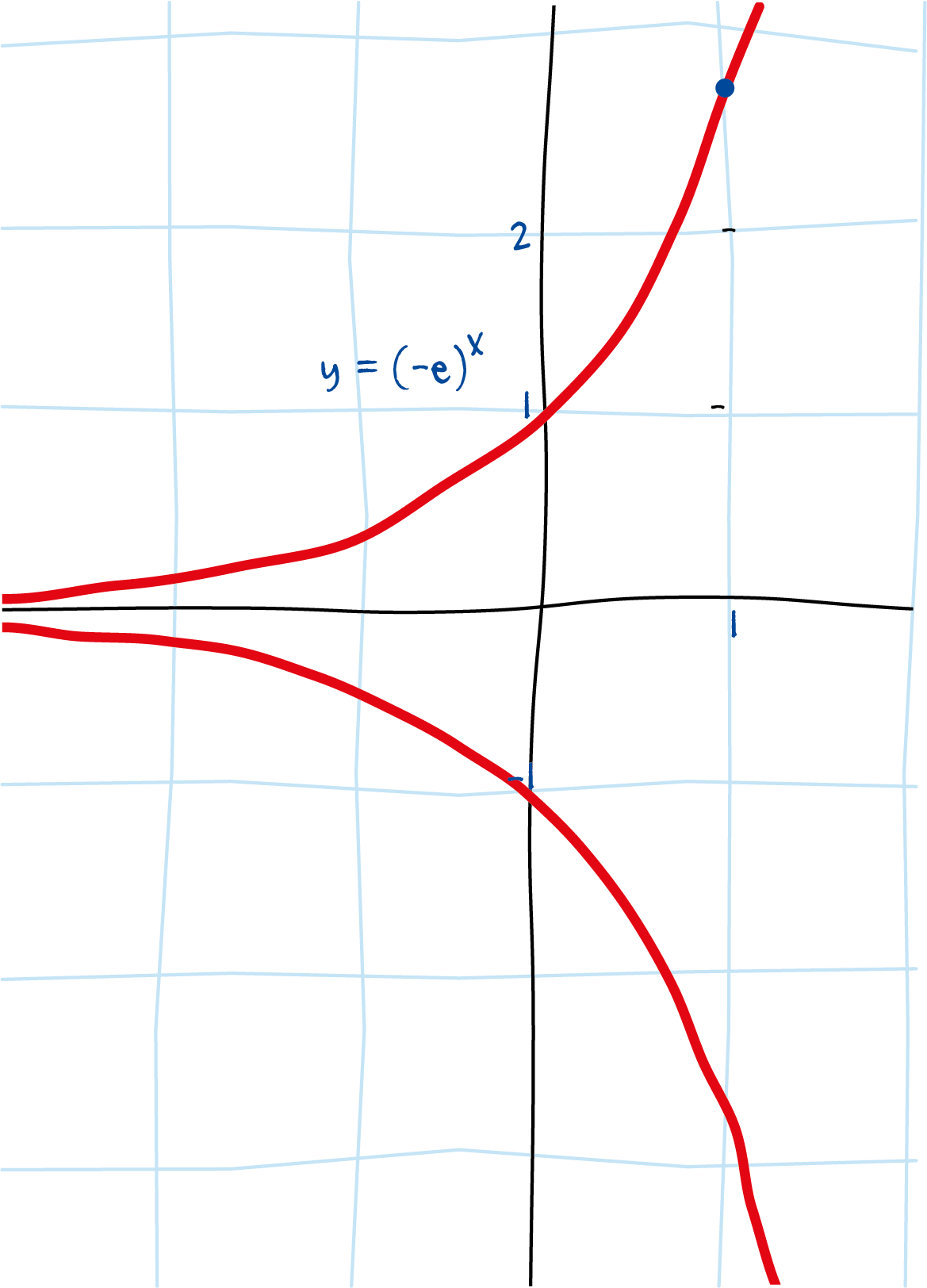
De grafiek ziet eruit als de functie $e^x$ samen met zijn spiegelbeeld ten opzichte van de $x$-as, maar dat kan natuurlijk niet kloppen. Immers, dat zou betekenen dat $(-e)^x$ voor elke $x$ twee verschillende, en tegengestelde, waarden heeft.
Wat is hier aan de hand?
Eerst halen we, net als boven, de factor $(-1)^x$ los: $(-e)^x = (-1)^x \cdot e^x$. Ook kijken we alleen naar $x$ tussen $0$ en $1$, want voor $x > 1$ kunnen we schrijven:
$(-1)^x = (-1)^{n+d} = (-1)^n \cdot (-1)^d$
waarbij $x = n + d$, met $n$ een geheel getal en $0 < d < 1$.
De factoren $(-1)^n$ en $e^x$ geven geen problemen, de moeilijkheid zit alleen in $(-1)^d$. De exponent $d$ is hier een breuk $p/q$ met $p < q$ en $q$ oneven. Een grafiek met een groot aantal waarden van $(-1)^d$ ingevuld zou er zo uit zien:
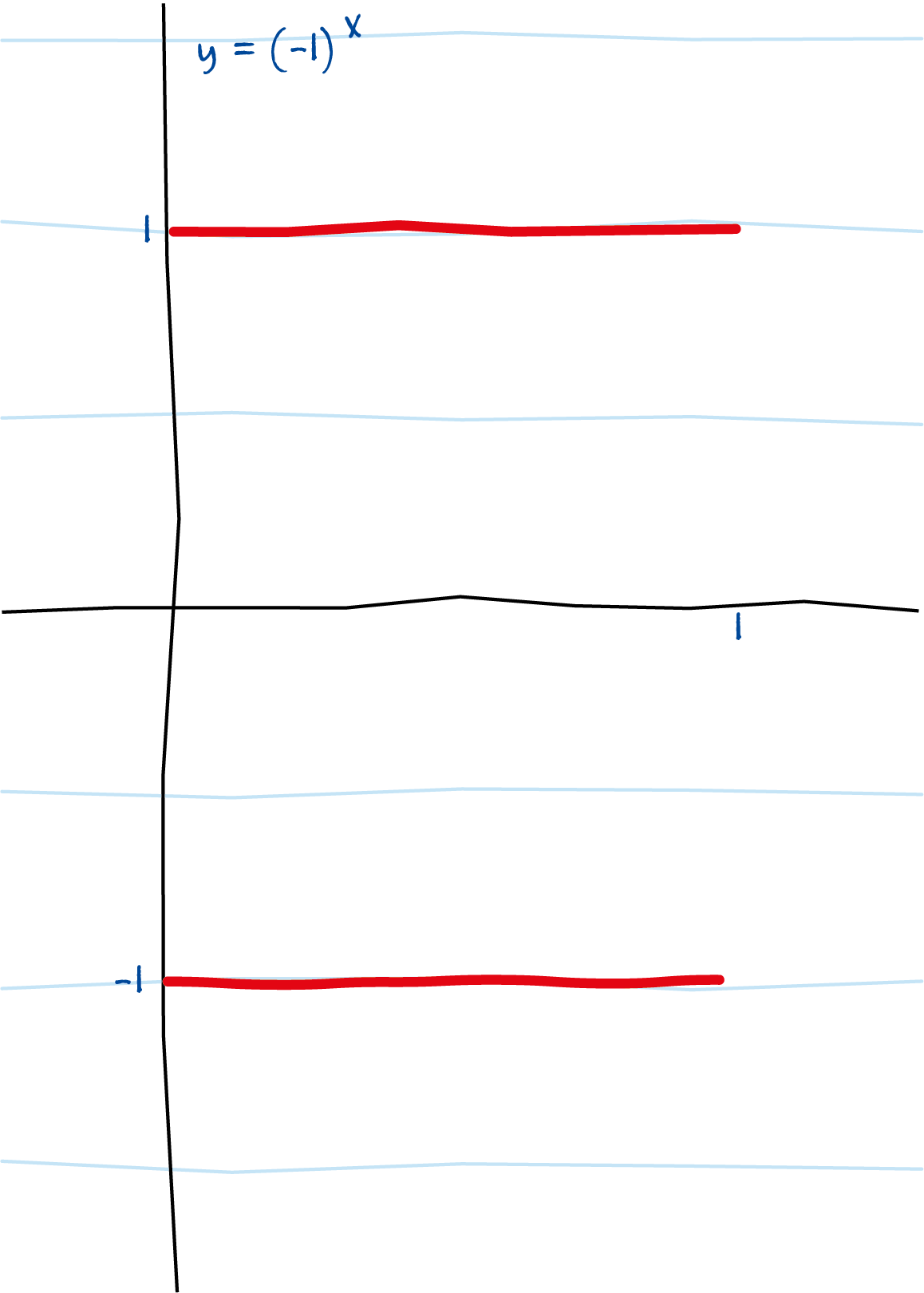
Ook hier die schijnbare spiegeling in de $x$-as, van de horizontale lijn $y = 1$. Maar met die beide lijnen $y = 1$ en $y = -1$ is iets heel vreemds aan de hand. Bekijk twee rationale waarden van $x$ die dicht bij elkaar liggen, zoals $113/137$ en $114/137$. De eerste teller is oneven, dus $(-1)^{\frac{113}{137}} = -1$. De tweede teller is even, dus $(-1)^{\frac{114}{137}}=1$. We zien dat de waarde van $(-1)^x$ over een heel kort interval (lengte $\frac{1}{137} = 0{,}007299\ldots$ in decimale notatie) van $-1$ naar $1$ verspringt. Wat gebeurt er in die ruimte tussen $113/137$ en $114/137$? Een normale, 'nette' (continue en differentieerbare) functie zou in een zeer steile lijn, bijna verticaal, omhoog lopen van $-1$ naar $1$.
Dat is echter niet wat er gebeurt. Om verder in te zoomen op dit intervalletje vermenigvuldigen we in beide breuken teller en noemer met drie: $113/137 = 339/411$ en $114/137 = 342/411$. De breuken $340/411$ en $341/411$ liggen nu tussen $113/137$ en $114/137$ in en zijn niet vereenvoudigbaar. Bovendien hebben we, wegens de even, respectievelijk oneven teller weer $(-1)^{340/411} = 1$ en $(-1)^{341/411} = -1$.
De waarde van $(-1)^d$ slaat dus tussen $(-1)^{113/137} = -1$ en $(-1)^{114/137} = 1$ nog een keer extra om, van $1$ naar $-1$. Je kunt deze truc herhalen met de breuken $340/411$ en $341/411$: $340/411 = 1020/1233$ en $341/411 = 1023/1233$, dus liggen de niet-vereenvoudigbare breuken $1021/1233$ en $1022/1233$ daar tussenin, en slaat de waarde van $(-1)^d$ ook daartussen om.
Iedere keer zoom je als het ware met een factor drie in op twee nabijgelegen punten in de grafiek van $(-1)^d$, en ziet dan een extra omslagpunt. Het moge duidelijk zijn, dat er geen grens aan dit inzoomen zit; wat we eerst aanzagen voor twee continue horizontale lijnen, is in feite een (aftelbaar) oneindig grote verzameling losse punten, die op elk interval oneindig vaak op en neer springt tussen $1$ en $-1$.
De domeinen van de functies $(-1)^d$ en $(-e)^x$ zijn niet van die mooie intervallen die je normaal ziet maar verzamelingen rationale getallen die na vereenvoudiging een oneven noemer hebben. Als je hun grafieken wilt tekenen moet je eigenlijk voor elk punt apart een stip zetten: op hoogte $1$ als de teller even is en op hoogte $-1$ als de teller oneven is. Maar omdat die getallen zo dicht op elkaar liggen lijken die stippen te versmelten tot twee lijnstukken of krommen.
En hoe nu verder?
Is er een oplossing/definitie voor de waarde van $(-1)^x$ is als $x$ rationaal is met een even noemer, of als $x$ niet rationaal is? Een hint voor wat er gaat gebeuren kun je bijvoorbeeld op www.wolframalpha.com zien of in een wat geavanceerder rekenprogramma op je computer.
Als je $(-1)^{1{,}2}$ en $(-1)^{1{,}3}$ intikt krijg je iets andere antwoorden dan we hierboven hebben gezien:
$(-1)^{1{,}2} = -0{,}809017\ldots - 0{,}587785\ldots i$
en
$(-1)^{1{,}3} = -0{,}587785\ldots - 0{,}809017\ldots i$
Beide hebben een antwoord, maar $(-1)^{1{,}2}$ klopt niet met de $1$ die we hierboven vonden.
Wat is hier aan de hand? Dat komt in een later artikel aan bod.
Drukte op de getallenlijn
Tussen twee rationale punten op de getallenlijn, zoals $113/137$ en $114/137$, liggen altijd weer andere rationale punten, zoals we boven gezien hebben. Er zit geen grens aan hoe groot de tellers en noemers van die breuken mogen worden, dus er liggen oneindig veel rationale punten op het lijnstuk $[0, 1]$. Je denkt dan allicht dat al die rationale punten het hele lijnstuk vullen, en dat er niets meer bij kan.
Dit is niet waar: op dat lijnstuk liggen zelfs nog meer niet-rationale punten! Tussen twee rationale punten ligt altijd nog een niet-rationaal punt, maar omgekeerd ligt tussen twee niet-rationale punten ook altijd een rationaal punt. Beide verzamelingen punten zijn oneindig groot, maar een lijnstuk bevat 'aftelbaar oneindig' veel rationale punten, en 'overaftelbaar oneindig' veel niet-rationale punten.
De $x$-coördinaat van laatstgenoemde punten kun je niet schrijven als een breuk $p/q$ van gehele getallen. In decimale notatie zou de $x$-coördinaat een getal zijn met oneindig veel cijfers achter de komma, die zich nooit herhalen. Voorbeelden zijn $\sqrt{2}$ (en alle andere wortels van getallen die geen volkomen kwadraat zijn), $\pi$ en $e$.
| Dat er meer niet-rationale getallen dan rationale getallen zijn werd in 1873 ontdekt door Georg Cantor. Je kunt over die ontdekking lezen in Pythagoras 57-4, april 2018 | ||
