In dit ‘nieuwe handelsreizigersprobleem’ mag je de wegen zelf bepalen. De steden liggen echter op de ongunstigste plekken in een land. We bekijken het nieuwe handelsreizigersprobleem eerst voor vijf steden. Denk je zich voor het gemak het land in als een vierkant. De meest ongunstige ligging van de vijf steden is dan die waarbij er één in het midden ligt en de andere vier op de hoekpunten van het vierkant, zoals in figuur 1.

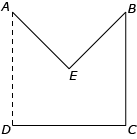
Figuur 1

Als de handelsreiziger bij deze vijf steden de kortste route wil afleggen, dan is dat bijvoorbeeld $AEBCD,$ in rechte lijnen (‘wegen’). Stellen we de lengte-eenheid $AB$ op $1,$ dan volgt een totale lengte $($via $AE, EB, BC$ en $CD): \frac12\sqrt2 + \frac12\sqrt2 + 1 + 1 = 2 + \sqrt2 \approx 3{,}414.$ Alle andere routes door de vijf punten hebben een even grote of grotere lengte dan die waarde.

In Pythagoras 56-2 was de laatste vervolgvraag hoe de ligging en minimale afstand waren voor zes steden. In het antwoord stond alleen dat die minimale afstand $3{,}5$ was. De bijhorende route was wel na te gaan. De afstand $3{,}5$ ontstaat door weer vier hoekpunten te nemen en als vijfde en zesde punt $(\frac38, \frac12)$ en $(\frac58, \frac12).$ In figuur 2 zijn twee optimale routes, beide met die afstand $3{,}5$ na te gaan. De ene gaat via $AEFBCD$ en de andere via $AEDCFB.$ (De afstand $AB$ is weer $1,$ nu verdeeld in acht stukjes.)

Figuur 2

De afstand $AE$ is, met de stelling van Pythagoras, precies $\frac58{:} \sqrt{(\frac38)^2 + (\frac12)^2} = \sqrt{\frac{25}{64}}.$ Bovengenoemde twee routes hebben dan beide inderdaad een lengte van $3{,}5{:} \frac58 + \frac14 + \frac58 + 1 + 1$ (via $AEFBCD$) en $\frac58 + \frac58 + 1 + \frac58 + \frac58$ ($AEDCFB$).

Maar het kan beter! Hoe? Daarvoor moet je twee andere ‘middenpunten’ aanwijzen. Er zijn dus twee punten die nog iets ongunstiger zijn voor de handelsreiziger. De minimale route wordt dan net iets langer dan $3{,}5.$

Welke twee punten zijn dat?

Antwoord

Het antwoord is dus niet het in Pythagoras 56-2 (indirect) gegeven tweetal puntenparen $(\frac{3}{8},\frac{1}{2})$ en $(\frac{5}{8}, \frac{1}{2})$ met minimale route $3{,}5$.

Maar ook niet puntenparen  $(\frac{2}{5}, \frac{3}{5})$ en $(\frac{3}{5}, \frac{2}{5})$, getoond in figuur 3. (Merk op dat beide punten op de lijn $x + y = 1$ liggen.) Via de route $AEDCFB$ is de afstand in dit geval $0{,}8\sqrt{2} + 0{,}4\sqrt{13} + 1 = 3{,}5735\ldots,$ en via route $AEFBCD$ iets minder, dus optimaal voor onze handelsreiziger: $0{,}6\sqrt{2} + 0{,}2\sqrt{13} + 2 = 3{,}56963\ldots.$ Maar het is wel meer dan de $3{,}5$ via de eerdere keuze van de punten $E$ en $F$, op de lijn $y = \frac{1}{2}$.

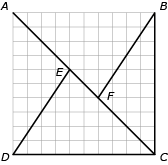
Figuur 3

Maar er is een nog iets langere minimale route! Deze loopt via het punt $E$ met $x$-coördinaat $\left(5+3\sqrt{2}-\sqrt{11-2\sqrt{2}}\right):16\approx 0{,}399$ en $y$-coördinaat $1 - x \approx 0{,}601$. Het punt $E$ ligt dus op de lijn  $y = 1 - x$, op de lijn door $A$ en $C$. Het punt $F$ ligt ook op die lijn, puntgespiegeld in $(\frac{1}{2},\frac{1}{2}).$ Beide punten zijn te vinden door $E$ als $(x, y)$ en dus $F$ als $(1 - x, 1 - y)$ te kiezen en de beide routes ($AEDCFB$ en $AEFBCD$) in lengte aan elkaar gelijk te stellen. We krijgen dan de vergelijking

$$(AE + CF) + (ED + FB) + DC = AF + FB + (BC + CD)$$

$$2\sqrt{x^2+(1-y)^2} + 2\sqrt{x^2+y^2} + 1 = \sqrt{(1-x)^2+y^2} + \sqrt{x^2+y^2} + 2.$$

Omdat $y = 1 - x$, volgt

$$2x\sqrt{2}+2\sqrt{x^2+(1-x)^2} + 1 = (1-x)\sqrt{2}+\sqrt{x^2+(1-x)^2}+2.$$

Vereenvoudigen leidt tot

$$\sqrt{x^2+(1-x)^2}+3x\sqrt{2}-1-\sqrt{2}=0.$$

De wortelvorm herschrijvend en de andere drie termen naar rechts brengend, krijgen we

$$\sqrt{2x^2-2x+1}=-3x\sqrt{2}+1+\sqrt{2}. $$

Kwadrateren geeft, na enig sorteerwerk en uiteindelijk delend door $2$, de kwadratische vergelijking

$$8x^2-(5+3\sqrt{2})x+1+\sqrt{2}=0.$$

met als oplossing de genoemde waarde

$$x=\frac{5+3\sqrt{2}-\sqrt{11-2\sqrt{2}}}{16}=0{,}399002\dots.$$

(Hierin komt de zogeheten ‘geneste wortel’, in het Engels nested radical, $\sqrt{11-2\sqrt{2}}$ voor, die niet korter te schrijven is. Er zijn overigens gevallen waarin dat wél kan: $\sqrt{6+\sqrt{5}} = 1 + \sqrt{5};$ of $\sqrt{5-\sqrt{24}}=\sqrt{3}-\sqrt{2}.$ Misschien ook wel eens wat aparte aandacht waard in een ander stukje.)

De tweede coördinaat wordt

$$y=\frac{11-3\sqrt{2}+\sqrt{11-2\sqrt{2}}}{16}=0{,}600997\dots.$$

De routes door $E$ met deze $x$-coördinaat en $1 -x$ als $y$-coördinaat en puntgespiegelde $F$ hebben dan dezelfde lengte $L$ van (afgerond) $3{,}5713$, en dus langer dan $3{,}5$ en ook langer dan de afgeronde $3{,}56963$ van de route uit de figuur.

In gesloten vorm heeft de lengte van de kortste route de nogal ingewikkelde uitdrukking

$$L=\frac{1}{16}\left(12+10\sqrt{2}-2\sqrt{22-4\sqrt{2}}\right)+\frac{1}{8}\sqrt{204-40\sqrt{2}+12\sqrt{11-2\sqrt{2}}-12\sqrt{22-4\sqrt{2}}}+1.$$

Een tweede oplossing is natuurlijk ook het symmetrische geval met de puntenparen $(0{,}399; 0{,}399)$ en $(0{,}601; 0{,}601)$, beide op de lijn $y = x$. Ook dan heeft de optimale route uiteraard een lengte van (afgerond) $3{,}5713$.

Het wonderlijke van dit resultaat is dat de intuïtie je hier blijkbaar in de steek laat. Het is niet de simpele oplossing $E = (\frac{3}{8}, \frac{1}{2})$ en ook niet $E = (\frac{2}{5}, \frac{3}{5})$ als het optimale punt!

Met dit alles is nog niet bewezen dat de genoemde route ook echt de route is met de grootste afstand voor de handelsreiziger. Dat moet nog verder onderzocht worden.