In toepassingen van de wiskunde kun je vraagstukken tegenkomen die niet zijn aan te pakken 'volgens het boekje', met een afleiding die de exacte oplossing geeft. Of er is wel een exacte oplossing bekend, maar eentje in de vorm van een formule waarvan de numerieke waarde niet zomaar voorhanden is. De numerieke wiskunde gaat over berekeningen die in zulke gevallen de oplossing proberen te benaderen.

Dit en een volgend artikel duiken in numerieke nulpuntsbepalingen van functies. Als voor een functie $f$ en een getal $r$ geldt dat $f(r) = 0$, dan heet het getal $r$ een nulwaarde van $f$ en het punt $(r, 0)$ waar de grafiek van $f$ de $x$-as snijdt of raakt een nulpunt van $f$. In het spraakgebruik, en ook hier, wordt een nulwaarde ook een nulpunt genoemd.

Het gebruik van numerieke methoden zit vol met verborgen moeilijkheden. Ze werken meestal alleen goed als ze met beleid worden toegepast. Om daar niet in vast te lopen, kijken we alleen naar continue functies en naar nulpunten waar de functie van teken verandert en de grafiek de $x$-as dus snijdt, niet raakt. Dit is niet het geval als de functiewaarden rond het nulpunt groter (of kleiner) zijn en de grafiek dus een dal (of een top) op de $x$-as heeft.

Het belang van numerieke nulpuntsbenaderingen verduidelijken we met veeltermen, functies van de vorm $p(x) = a_nx^n+a_{n-1}x^{n-1}+ \dots + a_2x^2 + ax +a_0$. Voor veeltermen is er een stelling die zegt dat een veelterm van de $n^e$ graad ten hoogste $n$ reële getallen als nulpunten heeft. Denk aan de abc-formule voor kwadratische vergelijkingen die, afhankelijk van de waarden van $a$, $b$ en $c$, één, twee of geen reële oplossingen geeft. Daarmee vind je snel dat de oplossingen van $x^2 + 2x - 1 = 0$ gelijk zijn aan $r = -1 \pm \sqrt{2}$. Voor derde- en vierdegraadsvergelijkingen zijn er de formules van Cardano, waarmee je kunt laten zien dat de oplossingen van $x^3 - 3x + 1 = 0$ gelijk zijn aan $r = 2\cos(2\pi/9)$, $2\cos(4\pi/9)$ en $2\cos(8\pi/9)$. Maar wat heb je daaraan als je die getallen voor een praktisch probleem nodig hebt? Dan wil je ze tot op een paar decimalen bepalen, en dat doe je door de gevonden uitdrukkingen in je rekenmachine in te voeren. In de praktijk sla je de formules gewoon over en ga je direct op zoek naar numerieke benaderingen van de oplossingen.

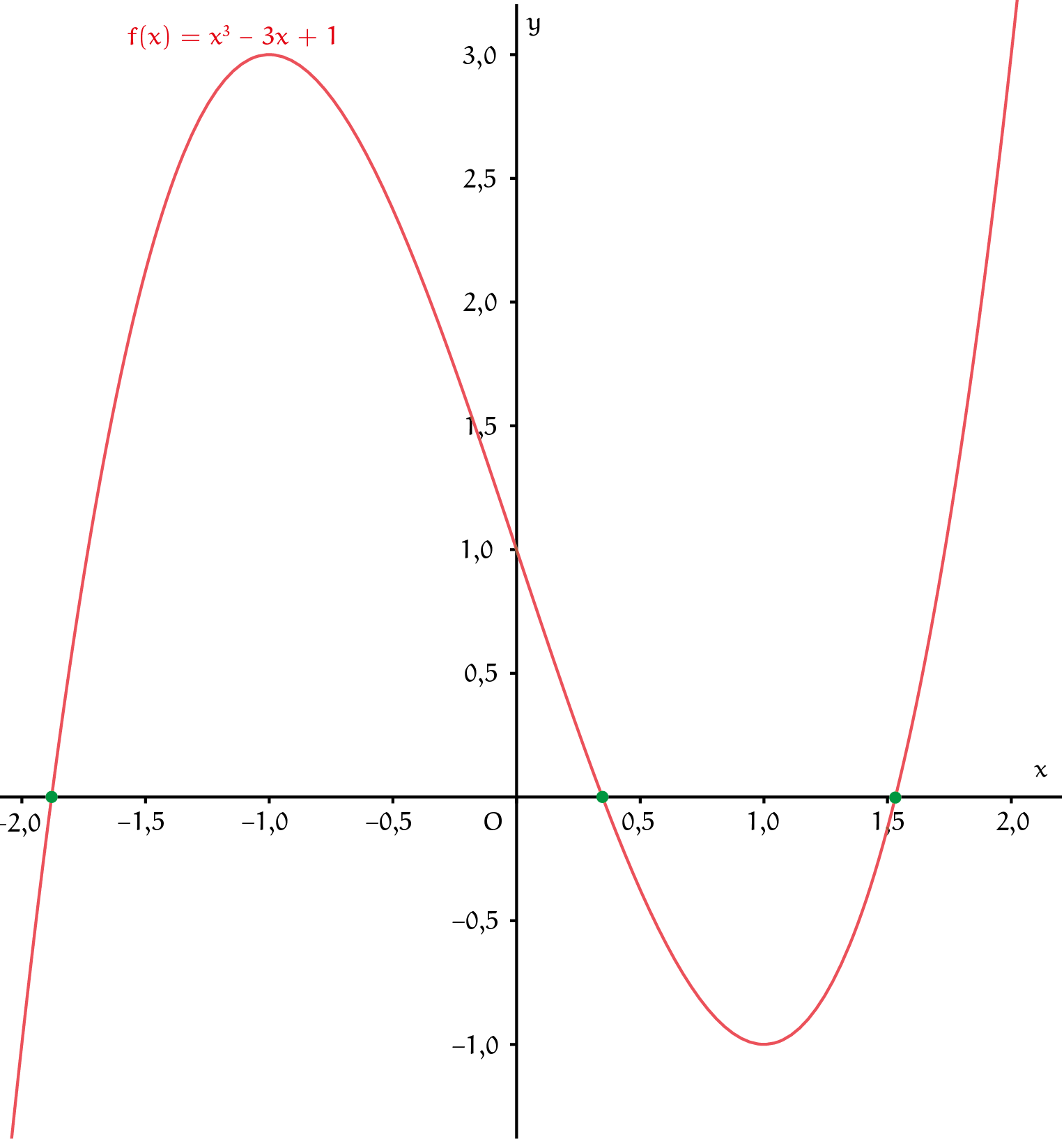
In dit artikel bespreken we hiervoor twee methoden: de bisectiemethode en de methode die regula falsi wordt genoemd. We passen ze toe op de derdegraadsveelterm $f(x) = x^3 - 3x + 1$. We vinden zo dus indirect ook benaderingen van de drie cosinuswaarden. Voor die waarden bestaan er geen worteluitdrukkingen zoals voor andere 'mooie' hoeken; je moet ze echt numeriek benaderen. Figuur 1 geeft de grafiek van de functie $f$, die inzicht geeft in de ligging van de nulpunten.

Een benadering $c$ van het (onbekende) nulpunt $r$ is een getal dat niet gelijk hoeft te zijn aan $r$, maar er weinig van afwijkt; we noteren dat als $c \approx r$. Benaderingsmethoden werken stapsgewijs. De stappen beogen steeds dichter bij het nulpunt te komen en worden voortgezet totdat de benadering goed genoeg is. Maar wat is goed genoeg? Hoe kun je vaststellen of een bepaalde, berekende $c$ een goede of minder goede benadering van $r$ is als $r$ onbekend is? Mogelijke voorwaarden zijn:

1. Als de functiewaarde $f(c)$ bijna gelijk is aan $0$, dan kun je $c$ opvatten als een benadering van het nulpunt $r$. Hoeveel $c$ van $r$ verschilt is niet zondermeer te zeggen. Dat hangt af van het verloop van de functie rond $r$. Hoe steiler de grafiek daar is, des te scherper is de voorwaarde.
2. Als opeenvolgende benaderingen $c$ weinig meer van elkaar verschillen, dan is het aannemelijk dat ze $r$ dicht zijn genaderd.
3. Als het zeker is dat $r$ is ingesloten tussen twee getallen $a$ en $b$ die weinig van elkaar verschillen, dan is elk getal $c$ tussen $a$ en $b$ een benadering van $r$. Hoe goed die benadering is, hangt af van het verschil $b - a$.

De biseCtiemethode

De eenvoudigste methode is de halverings- of bisectiemethode ('bisectie' betekent 'het in tweeën snijden'). Deze werkt met een interval waarvan bekend is dat er een nulpunt in ligt. Door achtereenvolgende halveringen wordt het nulpunt gevangen in een steeds kleiner deelinterval. 

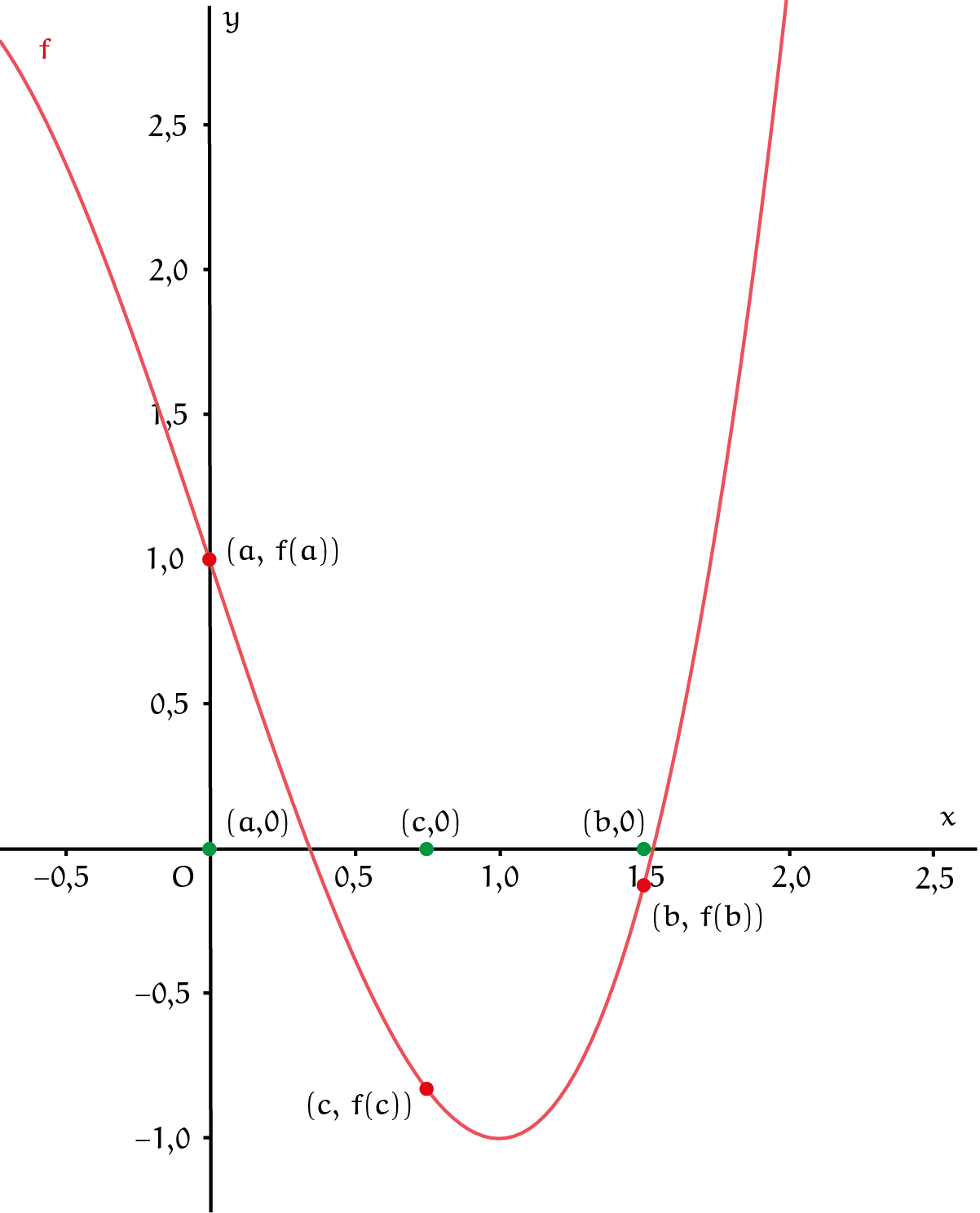
De bisectiemethode is alleen toepasbaar als de gegeven functie $f$ in het gezochte nulpunt van teken verandert en gaat uit van twee punten $(a, f(a))$ en $(b, f(b))$ op de grafiek van $f$ aan weerszijden van het te bepalen nulpunt $(r, 0)$ en aan weerszijden van de $x$-as. Dus $a < r < b$, en $f(a) > 0$ en $f(b) < 0$, of $f(a) < 0$ en $f(b) > 0$ (of kortweg $f(a) \cdot f(b) < 0$). Het midden $c = (a + b)/2$ van het interval $[a, b]$ wordt genomen als nulpuntsbenadering. Zie figuur 2. Als $f(c) = 0$, dan is de exacte waarde van het nulpunt gevonden: $r = c$. Voor $f(c) \neq 0$ wordt bepaald in welke helft $[a, c]$ of $[c, b]$ van $[a, b]$ het nulpunt ligt door de tekens van $f$ in $a$, $b$ en $c$ te vergelijken. Als $f(a)$ en $f(c)$ tegengesteld teken hebben, dan ligt het nulpunt $r$ in $[a, c]$, en anders hebben $f(c)$ en $f(b)$ tegengesteld teken en ligt $r$ in $[c, b]$. De volgende benadering is het midden van het deelinterval $[a, c]$ of $[c, b]$ waarin $r$ ligt. Enzovoort. Deze berekening wordt herhaald totdat de lengte van het overblijvende interval klein genoeg is.

Hieronder staat de bisectiemethode in de vorm van een pseudocode die je gemakkelijk kunt omzetten in een programmeertaal zoals Python. Dit stukje code wordt herhaald uitgevoerd totdat een aanvaardbare uitkomst is verkregen. In deze code zijn $a$ en $b$ steeds de eindpunten van het interval $[a, b]$ waarop $f$ van teken verandert en dat dus een nulpunt bevat. Dit is aanvankelijk het gekozen startinterval. Na iedere iteratie is $[a, b]$ die helft van het vorige interval dat het nulpunt bevat. Dus $a$ en $b$ zijn geen constanten, maar variabelen: in iedere iteratie wordt de waarde van $a$ of van $b$ aangepast. De berekening stopt als $f(c) = 0$ of als $(b - a)/2$ niet groter is dan een vooraf gekozen klein getal $0 < \delta \ll 1$ (voorwaarde (3), het teken $\ll$ betekent 'veel kleiner dan'). Omdat $a < r < c$ of $c < r < b$ geldt, wijkt de gevonden benadering $c$ dan niet meer dan $\delta$ af van het gezochte nulpunt $r : | r - c | \le (b - a)/2 \le \delta$.

{Gegeven: functie f, startpunten a en b, 0 < δ << 1}
fb = f(b)
c = (a + b)/2
fc = f(c)
Zolang fc ≠ 0 en (b – a)/2 > δ
      Als teken(fc) ≠ teken(fb), dan
            a krijgt de waarde van c
      anders
            b krijgt de waarde van c
            fb krijgt de waarde van fc
      c = (a + b)/2
      fc = f(c)
{Uitkomst: c met f(c) = 0 of (b – a)/2 ≤ δ}

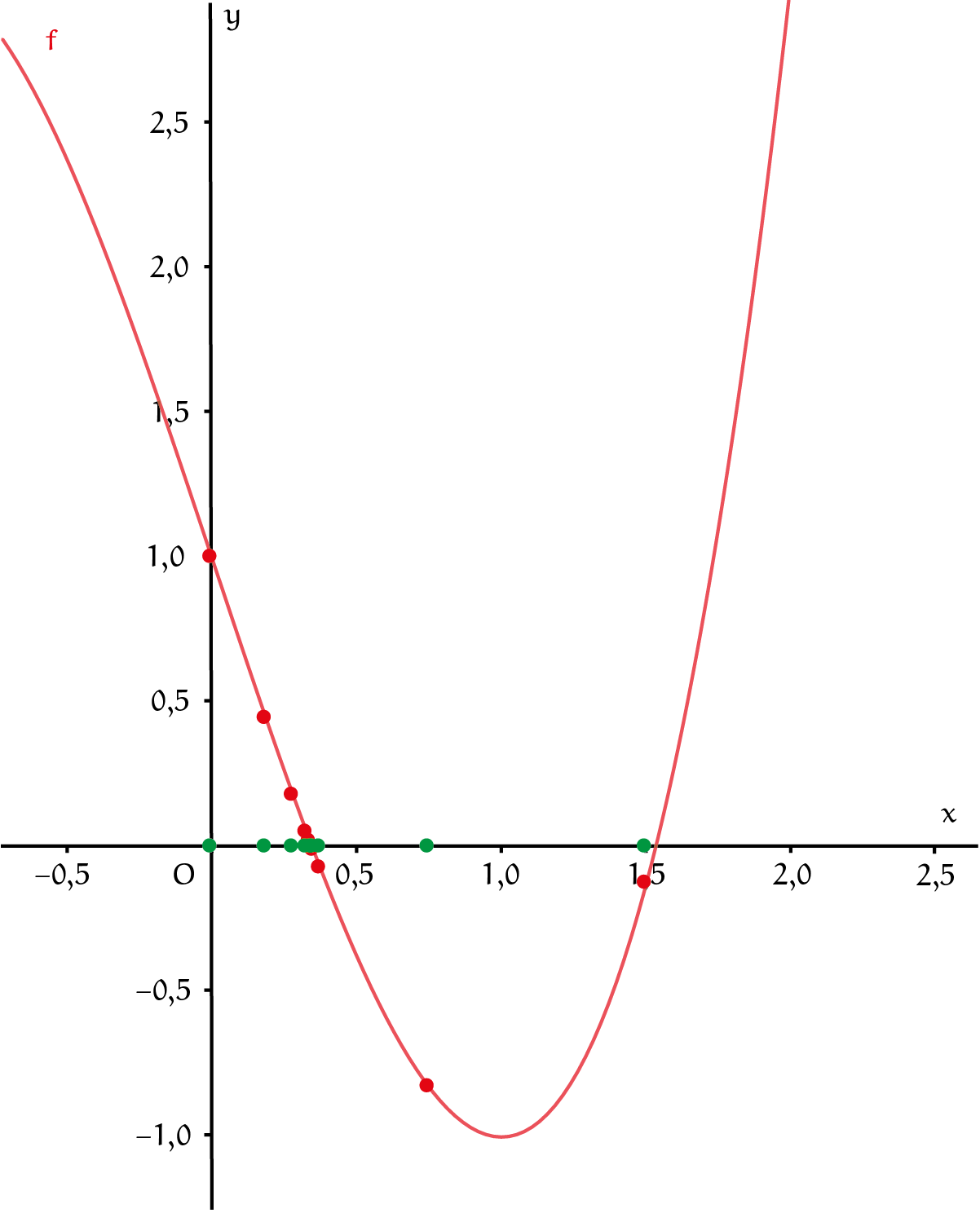
De bisectiemethode geeft gegarandeerd een nulpuntsbenadering met de gewenste nauwkeurigheid door voldoende iteraties uit te voeren. Het benodigde aantal volgt uit de lengte van het startinterval en de waarde van $\delta$. Je kunt ook een vast aantal iteraties instellen en de uitkomsten onderzoeken. Voor $f(x) = x^3 - 3x + 1$ en startpunten $a = 0$ en $b = 1{,}5$ geven figuur 3 en tabel 1 een aantal iteraties van de bisectiemethode gericht op het middelste nulpunt. Dit blijkt $r \approx 0{,}347$ te zijn (en dus $\cos(4\pi/9) \approx 0{,}174$).

Opgave 1 Uitgaande van een startinterval met lengte $s$ en door halvering in iedere iteratie, is in de $n^e$ iteratie de lengte teruggebracht tot $\left(\tfrac{1}{2}\right)^{n-1}s$. De benadering is goed genoeg wanneer $\left(\tfrac{1}{2}\right)^ns \le \delta$. Leid af dat dit wordt bereikt zodra $n \ge \log(\tfrac{s}{\delta})/\log(2)$.

 

$\color{white}{Iteratie}$	$\color{white}{Bisectie}$	$\color{white}{Regula falsi}$
$1$	$0{,}75$	$1{,}33333333333333333$
$2$	$0{,}375$	$0{,}8181818181818181$
$3$	$0{,}1875$	$0{,}42907801418439717$
$4$	$0{,}28125$	$0{,}355127249018671$
$5$	$0{,}328125$	$0{,}3479610792736418$
$6$	$0{,}3515625$	$0{,}34735210690679696$
$7$	$0{,}33984375$	$0{,}34730102653422457$
$8$	$0{,}345703125$	$0{,}3472967466813742$
$9$	$0{,}3486328125$	$0{,}3472963881202459$
$10$	$0{,}34716796875$	$0{,}34729635808064296$
$11$	$0{,}347900390625$	$0{,}347296355563981$
$12$	$0{,}3475341796875$	$0{,}3472963553531398$

 

Opgave 2 Pas de Python-programma's (je vindt ze hieronder via de knop [Bekijk oplossing]) voor de bisectiemethode toe voor de andere twee nulpunten van $f(x) = x^3 - 3x + 1$ door het startinterval aan te passen. Neem ook een aantal verschillende startintervallen die alle drie de nulpunten bevatten en vergelijk de uitkomsten. En je kunt natuurlijk ook andere veeltermen beschouwen.

De regula falsi methode

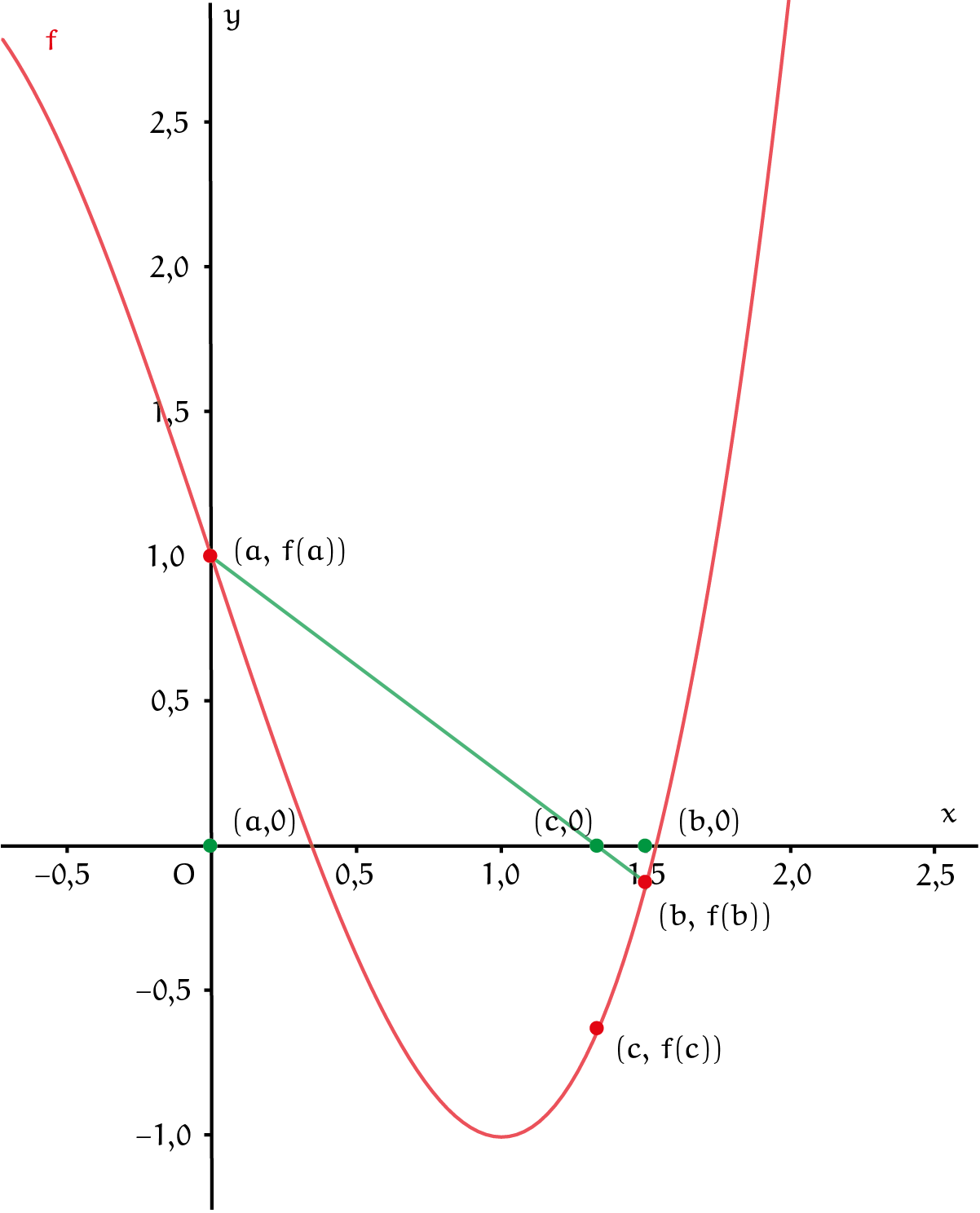
De regula falsi methode werkt net als de bisectiemethode met een interval waarin zich zeker een nulpunt bevindt. Ze is dus ook alleen toepasbaar daar waar de functie van teken wisselt, en gaat ook uit van twee punten $(a, f(a))$ en $(b, f(b))$ op de grafiek aan weerszijden van het nulpunt en aan weerszijden van de $x$-as. In deze methode is de nulpuntsbenadering het nulpunt van de lineaire functie tussen $(a, f(a))$ en $(b, f(b))$. In grafiekvorm betekent dit dat er tussen deze twee punten een recht lijnstuk wordt getrokken en het punt berekend wordt waar dat lijnstuk de $x$-as snijdt. Het lijnstuk heeft richtingscoëfficiënt $\frac{f(b)-f(a)}{b-a}$ en als vergelijking:

$y=f(a)+\frac{f(b)-f(a)}{b-a}(x-a)$.

Het snijpunt $(c,0)$ van het lijnstuk en de $x$-as volgt voor $y=0$:

$c=a-f(a)\frac{b-a}{f(b)-f(a)}=\frac{af(b)-bf(a)}{f(b)-f(a)}.$

$(\star)$

Zie figuur 4. Als $f(c) = 0$, dan is $r = c$. Anders wordt bepaald in welk deel $[a, c]$ of $[c, b]$ van $[a, b]$ het nulpunt $r$ ligt door de tekens van $f$ in $a$, $b$ en $c$ te vergelijken. Als $f(a)$ en $f(c)$ tegengesteld teken hebben, dan ligt $r$ in $[a, c]$, anders in $[c, b]$. De volgende benadering wordt berekend door $(\star)$ opnieuw te gebruiken op het interval waarin $r$ ligt. Enzovoort. Dus niet alleen de tekens van de functiewaarden maar ook de waarden zelf worden in de benadering betrokken. De regula falsi ('regel van de onware (positie)') geeft een 'valse' positie, maar herhaald toegepast uiteindelijk altijd een goede benadering van het nulpunt.

Hieronder staat de regula falsi methode in pseudocode. Wederom zijn $a$ en $b$ telkens de eindpunten van het interval met het nulpunt. De berekening stopt als $|f(c)|$ niet groter is dan een vooraf gekozen klein getal $\varepsilon$ (voorwaarde (1)).

{Gegeven: functie f, startpunten a en b, 0 < ε << 1}
fa = f(a)
fb = f(b)
c = (a*fb - b*fa)/(fb – fa)
fc = f(c)
Zolang |fc| > ε
      Als teken(fc) ≠ teken(fb), dan
            a krijgt de waarde van c
            fa krijgt de waarde van fc
      anders
            b krijgt de waarde van c
            fb krijgt de waarde van fc
      c = (a*fb - b*fa)/(fb – fa)
      fc = f(c)
{Uitkomst: c met |f(c)| ≤ ε}

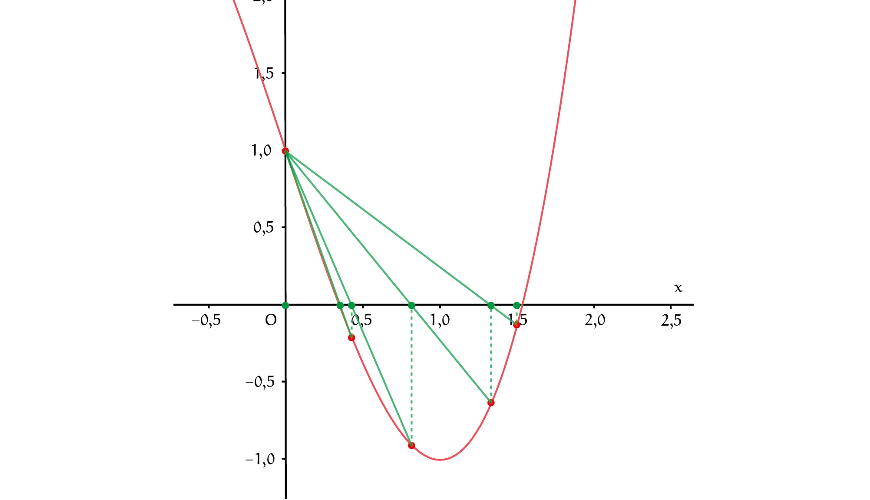
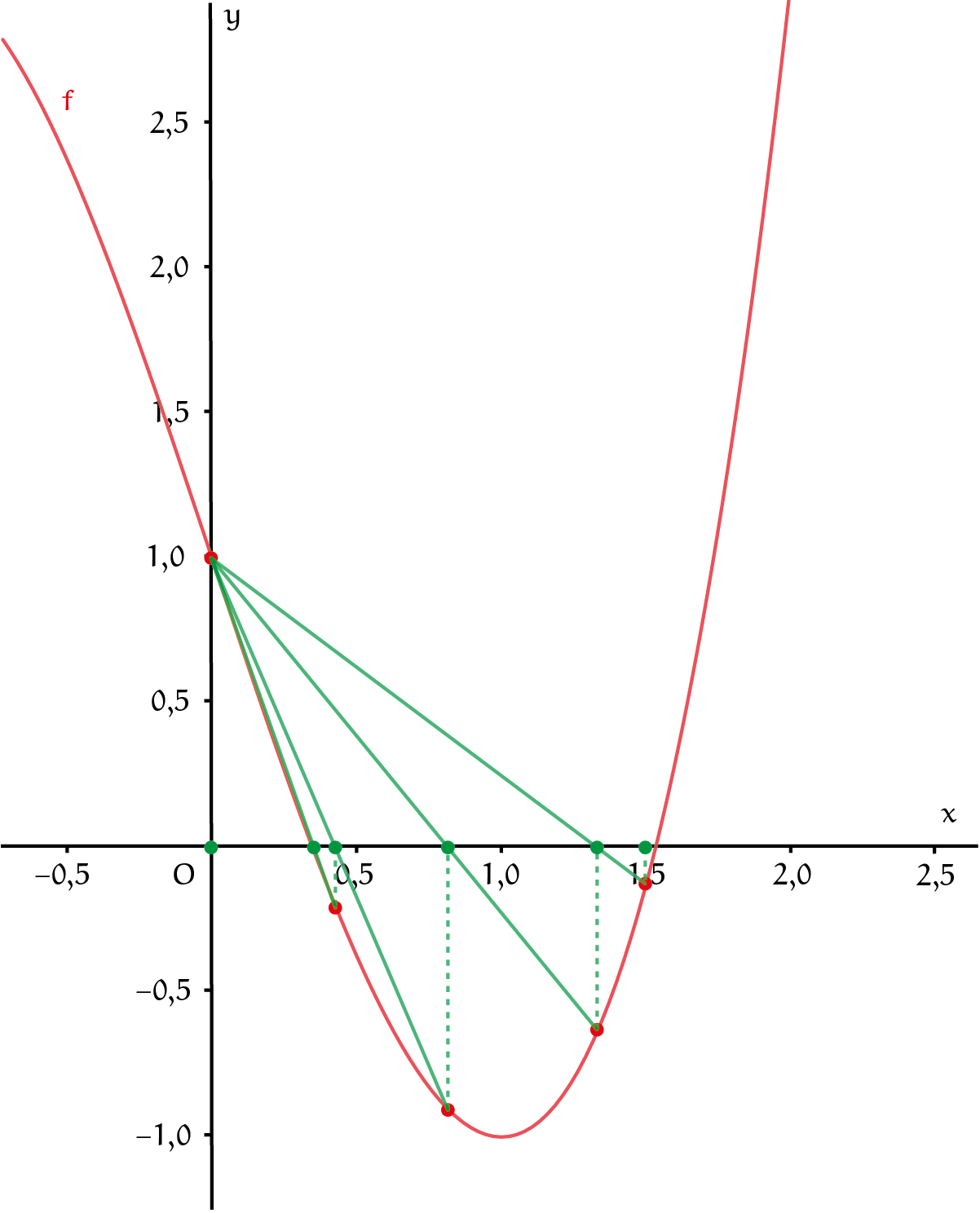
De voorwaarde om de berekening te stoppen kijkt naar de grootte van de functiewaarde $f(c)$ en niet naar de lengte van het interval $[a, b]$. Die lengte wordt weliswaar in iedere iteratie kleiner, maar hoeft niet naar $0$ te gaan zoals bij herhaalde halveringen. Dat hangt af van het verloop van de functie rond het nulpunt. Voor $f(x) = x^3 - 3x + 1$ en startpunten $a = 0$ en $b = 1{,}5$ geven figuur 5 en tabel 1 een aantal iteraties van de regula-falsimethode gericht op het middelste nulpunt. Het rechter eindpunt van het insluitende interval beweegt zich in de richting van het nulpunt, maar het linker eindpunt blijft op zijn plek. Afschattingen voor $|r - c|$ zijn dan lastig, omdat $b - a$ niet maatgevend is. Wel geldt $f(c) \approx f'(r)(c - r)$ dichtbij $r$, vandaar de keuze voor de voorwaarde $|f(c) | < \varepsilon \ll 1$. De regula falsi methode komt in veel gevallen in minder iteraties dan de bisectiemethode op een goede benadering uit, omdat er meer informatie over de functie wordt meegenomen: in de berekening van de benadering komen functiewaarden voor en dat is bij de tweedelingen niet het geval. Het volgende artikel behandelt twee andere methoden die nóg beter zijn.

Opgave 3 Vergelijk met de Python-programma's voor $f(x) = 2x^3 - 4x^2 + 3x$ de snelheid (in termen van aantal iteraties) van de regula falsi methode met startpunten $a = -1$ en $b = 1$ en met startpunten $a = -0{,}1$ en $b = 1$.