Het is hier in Pythagoras al eens eerder aangestipt: Borromeaanse ringen zijn drie met elkaar verstrengelde ringen die niet los te maken zijn zonder knippen. Als je om het even welke van de drie ringen zou doorknippen en wegnemen komen de twee overgebleven ringen volledig vrij te liggen. Anders dan de benaming en figuur 1A aangeven, is dat onmogelijk met drie cirkels te realiseren. Met drie rechthoeken lukt dat wel, zoals de alom bekende constellatie in figuur 1B laat zien. Je kunt dat gemakkelijk controleren met drie grote paperclips, zoals de eindredacteur van Pythagoras mij toonde toen dit eerder in Pythagoras 61-1 aan de orde kwam (figuur 1C).

De drie rechthoeken in figuur 1B bestaan uit houten balkjes met een vierkante doorsnede die net als een lijstje van een schilderij in gewoon verstek onder $45^{\rm o}$ zijn gezaagd en geschilderd. Daar op voortbordurend zijn er op dezelfde manier andere constructies mogelijk zoals wiskunstenaar Koos Verhoeff (1927 – 2018) aantoonde (figuur 2). Figuur 3 is een variant op figuur 2B. Eenzelfde constructie, maar de vierkante balk is eerst $45^{\rm o}$ gedraaid alvorens hem onder een hoek van $45^{\rm o}$ door te zagen om passende balkjes te maken.

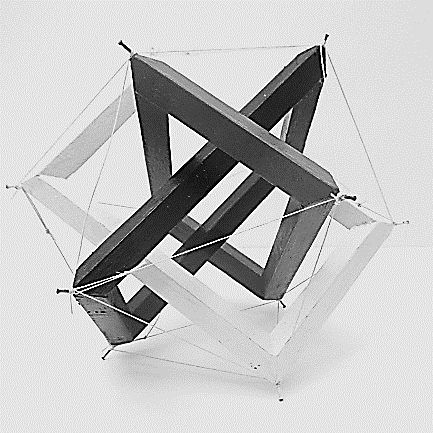
Opgave 1 Bepaal de (maximale) lengte van de balkjes in de figuren 1B en 2, anders gezegd: bepaal de lengte van de langste zijde(n).

Figuur 4 is een opengewerkte versie van figuur 1B. Het Borromeaanse drietal rechthoeken zit ineengeklemd om een rood kubusje. Ze hebben geen contact met elkaar. Ze staan onderling loodrecht op elkaar en hun middelpunten vallen samen. Figuur 5 is daar weer een variant op. De opengewerkte rechthoeken zijn gouden rechthoeken. Dat zijn rechthoeken waarvan de zijden zich verhouden volgens de gulden snede. De gulden snede is de verdeling van een lijnstuk in twee delen waarbij het grote deel zich verhoudt tot het kleine als het hele lijnstuk tot het grote deel (figuur 6).

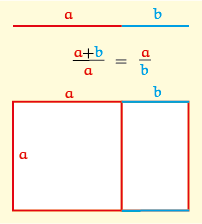
Opgave 2 Bereken het gulden getal $\varphi = a/b$ door $a/b$ op te lossen uit $(a + b)/a = a/b$ in figuur 6.

Borromeaanse Gouden Rechthoeken

De gouden rechthoeken in figuur 5 bestaan uit vierkante balkjes. Alvorens ze door te zagen zijn ze eerst $45^{\rm o}$ gedraaid, net als de balkjes in figuur 3. Zo worden de twaalf hoekpunten van de drie rechthoeken ook echte punten. Door die hoekpunten onderling met touwtjes te verbinden wordt dit Borromeaanse drietal op zijn plaats gehouden. De lengte van die touwtjes is precies gelijk aan een korte rechthoekzijde. Zo spannen die drie loodrecht op elkaar staande Borromeaanse gouden rechthoeken een regelmatig twintigvlak of icosaëder op, zoals in figuur 7. Samen met de 6 korte rechthoekzijden vormen de 24 touwtjes de 30 ribben of randen van het regelmatig twintigvlak.

Opgave 3 Bepaal aan de hand van figuur 7 het aantal verschillende rechthoeken in een icosaëder. Toon aan dat dit inderdaad gouden rechthoeken zijn.

Fraaier en iets meer op vervormde cirkels lijkend wordt het met drie ruimtelijke twaalfhoeken (figuur 8). Ze bestaan elk uit 12 ruimtelijke trapezia.

 

Bekijk oplossing