Opgave 1

Figuur 1. Elk van de drie rechthoeken bestaat uit twee balkjes met een maximale lengte van 3 maal de dikte en twee balkjes met een maximale lengte van 5 maal de dikte van de gebruikte balk.

Figuur 2. De maximale lengte van alle balkjes is 4 maal de dikte van de gebruikte balk.

Opgave 2

$\frac{a+b}{a} = \frac{a}{b}$ kan worden geschreven als $1 + \frac{b}{a} = \frac{a}{b}$ met $\varphi = \frac{a}{b}$ wordt dit $1+\frac{1}{\varphi}=\varphi$ dat kan worden omgewerkt tot $\varphi+1=\varphi^2$ of $\varphi^2-\varphi-1=0$.

Toepassen van de abc-formule levert $\varphi=\frac{1\pm\sqrt{1+4}}{2}=\frac{1+\sqrt{5}}{2}=1{,}6180\ldots$.

De negatieve oplossing vervalt uiteraard want $\varphi$ is de verhouding van de lengten van twee lijnstukken.

Opgave 3

15 gouden rechthoeken (zoals aan het einde van deel 2 beschreven)

Voor een gouden rechthoek in een icosaëder zijn twee tegenover elkaar liggende zijden nodig. Omdat een icosaëder $30$ zijden heeft zijn er $\frac{30}{2}=15$ verschillende gouden rechthoeken mogelijk. De middelpunten van die $15$ gouden rechthoeken vallen samen met het middelpunt van de icosaëder.

Berekening

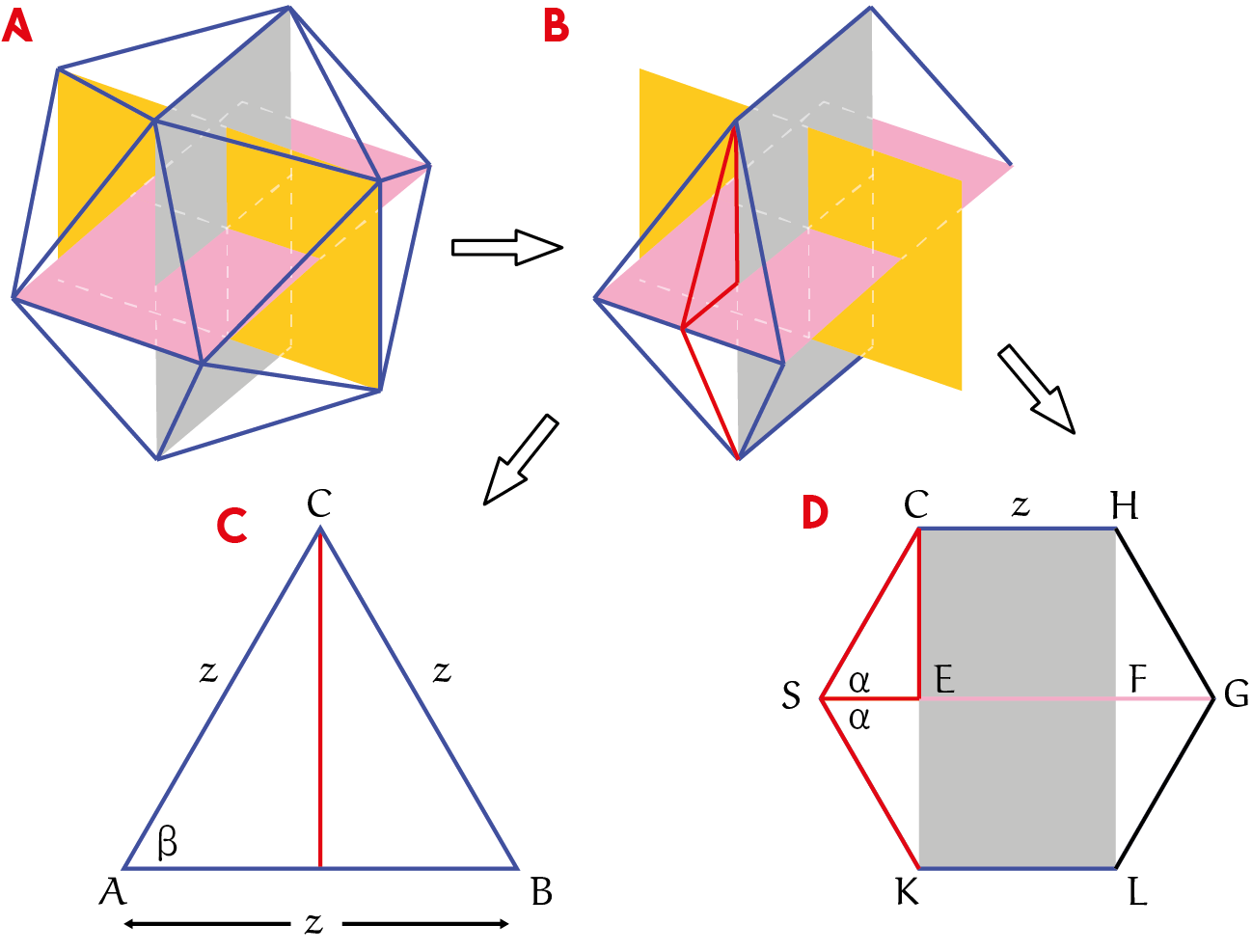
De icosaëder van figuur A wordt opgespannen door drie loodrecht op elkaar staande congruente rechthoeken met samenvallende middelpunten. In figuur C is de gelijkzijdige driehoek $ABC$ een zijvlak van de icosaëder met zijden $AB = BC = AC = z$. In driehoek $ASC$ is hoek $\beta$ gelijk aan $60^{\rm o}$. Dat betekent dat de lengte van lijnstuk $CS$ gelijk is aan $\tfrac{1}{2}z\sqrt{3}$. In een icosaëder is de hoek tussen twee zijvlakken afgerond $138^{\rm o}$.

In figuur D is dat hoek $CSK$. Dan is in driehoek $SEC$ hoek $\alpha$ afgerond $69^{\rm o}$.

Ook geldt in driehoek $SEC$ dat $CE = CS \times \sin(69^{\rm o} = \tfrac{1}{2}z\sqrt{3} \times 0{,}9336 = 0{,}8085 z$. Dan is $CK = 2 CE = 1{,}617 z$ en verhouden de zijden van de lichtgrijze rechthoek in figuur D zich afgerond als $1{,}617$. Daarmee is aangetoond dat die lichtgrijze rechthoek inderdaad een gouden rechthoek is. Hetzelfde geldt voor de gouden en roze rechthoeken in de figuren A en B.

Kijken (zoals aan het einde van deel 2 beschreven)

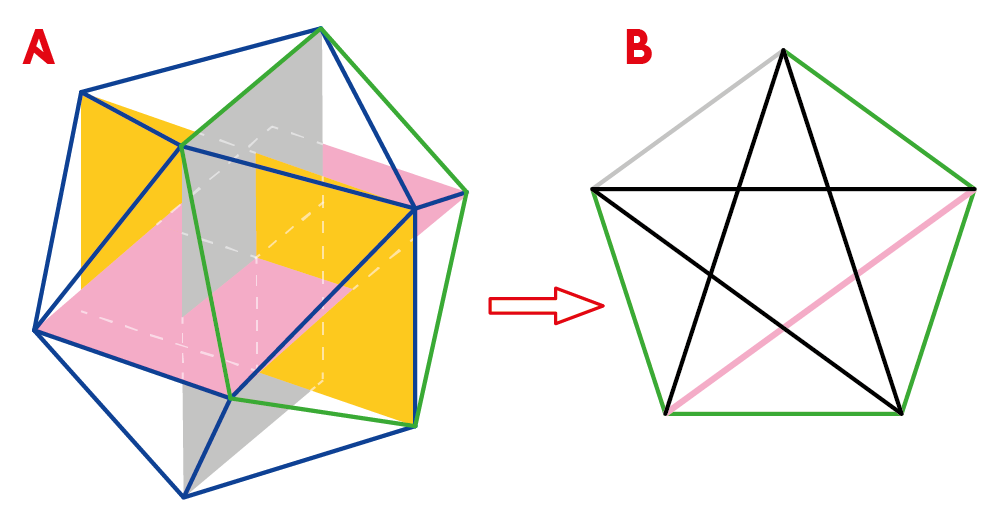
In de icosaëder van figuur A met daarin wederom de drie loodrecht op elkaar staande congruente rechthoeken, vormen de vijf groene zijden een regelmatige vijfhoek. In figuur B is die er apart uitgelicht. Daarin is de zijde die tevens een korte zijde is van de grijze rechthoek, grijs gekleurd. Ook is daarin de diagonaal die tevens een lange zijde is van de roze rechthoek, roze gekleurd. Gegeven is dat in een regelmatige vijfhoek een diagonaal en een zijde zich verhouden als het gulden getal. En daarmee verhouden de zijden van de rechthoeken in figuur A als het gulden getal. Het zijn dus gouden rechthoeken.