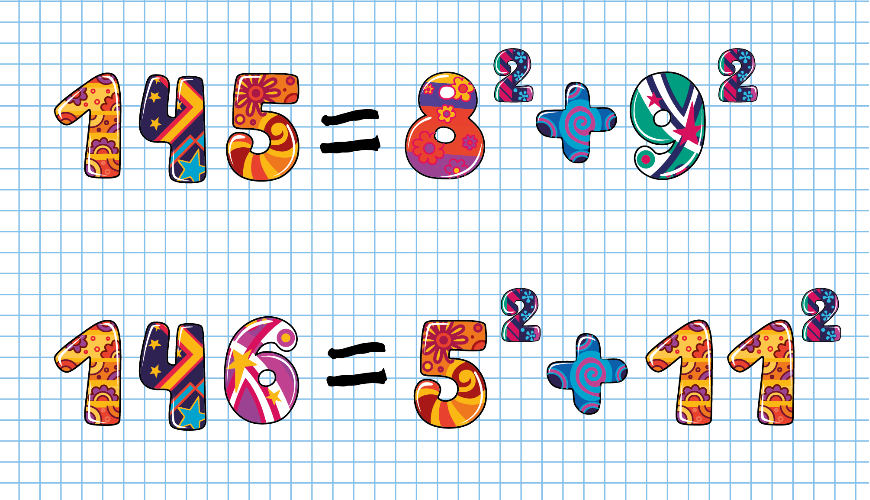
Opeenvolgende getallen die elk de som zijn van twee kwadraten
In een paar artikelen, in Pythagoras 55-1 en 55-2 uit 2015 is besproken hoe positieve gehele getallen te schrijven zijn als de som van twee of vier kwadraten. Met getallen die sommen zijn van kwadraten hebben de beroemdste wiskundigen zich beziggehouden, van Diophantus (ca. 3e eeuw na Christus) tot Gauss (1777-1855). In dit artikel gaan we ook zoiets onderzoeken. We kijken naar opeenvolgende gehele getallen die allemaal te schrijven zijn als de som van telkens twee kwadraten. Een voorbeeld: $145 = 8^2 + 9^2$ en $146 = 5^2 + 11^2$.
We stellen ons de volgende vragen: zijn er langere rijtjes van opeenvolgende getallen te vinden die allemaal de som van twee kwadraten zijn? Kunnen we die rijtjes net zo lang maken als we willen? Zo niet, wat is dan de maximale lengte? En zijn er dan van die rijtjes eindig of oneindig veel?
Wat is het maximaal aantal opeenvolgende sommen van kwadraten?
Een mooi voorbeeld is het drietal opeenvolgende getallen $72 = 6^2 + 6^2$, $73 = 3^2 + 8^2$ en $74 = 5^2 + 7^2$. Maar hoe je ook zoekt, met $71$ lukt het niet en met $75$ ook niet. Is de maximumlengte van zo'n rijtje misschien $3$?
Inderdaad, er zijn geen rijtjes van vier of meer opeenvolgende getallen die allemaal de som zijn van twee kwadraten. Om dat aan te tonen maken we gebruik van de volgende eenvoudige eigenschappen van kwadraten.
Voor een even getal $E = 2m$ geldt dat $E^2 = 4m^2$ een $4$-voud is $(4 - v)$. Voor een oneven getal $O = 2m + 1$ geldt dat $O^2 = (2m + 1)^2 = 4(m^2 + m) + 1$ een $4 - v + 1$ is. Stel nu eens dat er vier opeenvolgende getallen $g$, $g + 1$, $g + 2$ en $g + 3$ zijn die alle te schrijven zijn als de som van twee kwadraten. Eén van deze vier getallen is een $4 - v$, één een $4 - v + 1$, één een $4 - v + 2$ en één een $4 - v + 3$. Met $E$ een even getal en $O$ een oneven getal hebben we voor de som van twee kwadraten slechts drie mogelijkheden:
$E_1^2+E_2^2$: dit is een $4-v$
$E^2+O^2$: dit is een $4-v+1$
$O_1^2+O_2^2$: dit is een $4-v+2$
Dus een $4 - v + 3$ kan niet voorkomen. Het maximum aantal is daarmee drie opeenvolgende getallen. Het kleinste, dus $g$, moet een $4 - v$ zijn. Stel namelijk dat $g$ een $4 - v + 1$ is of een $4 - v + 2$. Dan is $g + 2$ of $g + 1$ een $4 - v + 3$ en dus geen element van het drietal. Het al genoemde drietal $72$, $73$, $74$ begint inderdaad met een $4 - v$. Een ander voorbeeld is $232 = 6^2 + 14^2$, $233 = 8^2 + 13^2$ en $234 = 3^2 + 15^2$: het laagste voorbeeld met telkens twee verschillende kwadraten.
oneindig veel drietallen?
Er zijn inderdaad oneindig veel opeenvolgende drietallen. Bekijk om dat aan te tonen als speciaal geval het getal $g = a^2 + a^2$, de som van twee dezelfde kwadraten. Neem vervolgens de twee getallen $a + 1$ en $a - 1$. De som van de kwadraten van deze twee getallen is $(a + 1)^2 + (a - 1)^2 = 2a^2 + 2 = g + 2$. We hebben dan al twee getallen, elk gelijk aan de som van twee kwadraten, die $2$ verschillen: $g$ en $g + 2$. Kunnen we, naast de paren $(a, a)$ en $(a + 1, a - 1)$, nu nog een paar vinden waarvan de som van de kwadraten $g + 1 = 2a^2 + 1$ is, zodat we dan het opeenvolgende drietal $g$, $g + 1$ en $g + 2$ hebben? Noem dit paar $(a + x, a - y)$. We zoeken dus $a$, $x$ en $y$ zo dat geldt: $g + 1 = (a + x)^2 + (a - y)^2 = 2a^2 + 1$ Maar in welk gebied moeten we de waarden van $x$ en $y$ zoeken? Dat is even wat puzzelen.
Opgave 1Ga zelf na dat:
|
We mogen dus de oplossing voor $a$ in ieder geval schrijven als:
$$a=\frac{x^2+y^2-1}{2(y-x)}\ge 0$$
want de noemer is niet $0$. Als $x$ en $y$ beide even of beide oneven zijn, is de teller hier oneven en de noemer even. Maar dat geeft geen gehele waarde van $a$. Dus we zien zo dat van het paar $x$ en $y$ er één even en één oneven is.
Voor $a > 0$ is de teller positief (want $x = y = 0$ kan niet) en daarmee ook de noemer, dus moet gelden $y > x$. Daarbij zou de som van $a^2$ en $(a + 1)^2$ al groter worden dan $2a^2 + 1$ en dat kan geen oplossing geven voor $g + 1$. En de som van $a^2$ en $(a – 1)^2$ wordt zelfs kleiner dan $g$ en geeft dus evenmin een oplossing. We zien dus dat in $g + 1$ één kwadraat groter en één kleiner moet zijn dan $a^2$. Voor $a > 0$ kunnen we ons daarom beperken tot het zoekgebied $0 < x < y$. (Kwadraten van negatieve getallen bieden natuurlijk dezelfde mogelijkheden als kwadraten van positieve getallen, dus we kunnen eigenlijk volstaan met waarden $y \le a$. Maar omdat we $a$ van tevoren niet kennen laten we voor het gemak deze bovengrens vallen; we kunnen daardoor dubbele oplossingen tegenkomen, met dezelfde combinatie van kwadraten in $g + 1$ en met $y > a$.)
Voor $a = 0$ geldt $x^2 + y^2 = 1$. De vier mogelijke oplossingen $(x = 0, y = \pm 1)$ en $(x = \pm 1, y = 0)$ geven allemaal dezelfde twee kwadraten. We kiezen dan $(x = 0, y = 1)$, waarmee we het zoekgebied uitbreiden tot $0 \le x < y$. Voor $x = 0$, $y = 1$ en dus $a = 0$ vinden we als oplossing het drietal $0 = 0^2 + 0^2$, $1 = 0^2 + 1^2$, $2 = 1^2 + 1^2$. Merk op dat in dit geval $a$ kleiner is dan $y$. Voor $x = 1$, $y = 2$ wordt de oplossing $a = 2$ en $8 = 2^2 + 2^2$, $9 = 0^2 + 3^2$, $10 = 1^2 + 3^2$. Zulke oplossingen met een $0^2$ erin vinden we misschien triviaal maar staan we wel toe. De eenvoudigste niet-triviale keuze is $x = 2$ en $y = 3$ (of $y = 9$) met $a = 6$ en dat levert het al bekende drietal $72$, $73$, $74$ op. Algemener kunnen we voor een willekeurige $x \ge 0$ de keuze $y = x + 1$ maken. Dat geeft: $a = x(x + 1)$.
Opgave 2Toon aan dat nu geldt: $$(a+x)^2+(a-y)^2=2a^2+1.$$ |
Daarmee hebben we voor elke $x \ge 0$ het opeenvolgende drietal:
$g = a^2 + a^2$
$g + 1 = (a + x)^2 + (a - x - 1)^2 = 2a^2 + 1$
$g + 2 = (a + 1)^2 + (a - 1)^2 = 2a^2 + 2$
Er bestaan dus oneindig veel drietallen $g$, $g + 1$ en $g + 2$ die telkens te schrijven zijn als sommen van twee kwadraten. De eerste zijn:
$x=0, y=1, a=0$, dit geeft $0$, $1$ en $2$
$x=1, y=2, a=2$, dit geeft $8$, $9$ en $10$
$x=2, y=3, a=6$, dit geeft $72$, $73$ en $74$
$x=3, y=4, a=12$, dit geeft $288$, $289$ en $290$
Dit kun je zelf zo voortzetten. Maar zo vinden we niet alle drietallen die beginnen met $g = 2a^2$. Immers, we hebben $y - x = p$ gelijk aan $1$ genomen.
Een algemenere aanpak
Hogere oneven waarden van $p$ kunnen natuurlijk nog meer oplossingen geven. Dan moeten we hierboven in de teller $x^2 + y^2 - 1$ de noemer $2(y - x) = 2p$ kunnen uitdelen. De factor $2$ zal altijd lukken, want de teller is even. Om te zien voor welke combinatie van $x$ en $y$ we ook de factor $p$ kunnen uitdelen is het handig van nu af aan die factor overal zichtbaar te maken. We schrijven daarom $x$ en $y = x + p$ nu als
$$x = rp + s, y = (r + 1)p + s.$$
Hierbij mag $r$ een willekeurig geheel getal $\ge 0$ zijn. Het getal $s$ is het restant dat in $x$ of $y$ na deling door $p$ overblijft, dus $s$ ligt tussen $0$ en $p - 1$. Na invullen krijgen we voor $a$ de algemene formule
$$a=\frac{\left(r^2+(r+1)^2\right)p^2+2(2r+1)ps}{2p} + \frac{2s^2-1}{2p}.$$
Ook hier hebben we de factoren $p$ die uitgedeeld kunnen worden in de eerste term van het rechterlid bij elkaar gezet. Omdat $p$ oneven is, is de teller van die eerste term wel oneven, dus na uitdelen van $2p$ wordt die eerste term halftallig. Als $a$ een geheel getal moet zijn, geldt dus de voorwaarde dat ook de tweede term halftallig is, dus dat $\left(2s^2 - 1\right)/p$ oneven is (eventueel wel negatief!). Daarmee wordt de algemene voorwaarde voor het restant $s$:
$$2s^2-1=pq.$$
met $p$ en $q$ beide oneven (en $q$ misschien negatief). Het handigste is nu om voor oplopende waarden van $s$ naar waarden voor $p > s$ en $q$ te zoeken. Voor $s = 0$ vinden we $p = 1, q = -1$ en krijgen we de hierboven al gevonden oneindige serie oplossingen weer terug: $a = x(x + 1)$ en $x = r = 0, 1, 2, 3, \dots$ met $r = 2$ en het drietal $72, 73, 74$ als eerste niet-triviale mogelijkheid.
Een uitgebreidere klasse oplossingen
Voor oplossingen met $s > 0$ kunnen we twee mogelijkheden onderscheiden.
| $\color{red}{i}$ |
$p > 1, q = 1$ dus $s^2 = (p + 1)/2$ |
Opgave 3Ga na dat voor $s=2$ geldt $p=7$ en dat voor $s=3$ geldt $p=17$. Bereken $a$ als functie van $r$ voor het geval $s=3$ en vind daaruit voor $r=0$ en $r=1$ de drietallen sommen van kwadraten. |
$\color{red}{ii}$ |
$p > 1$ en $q > 1$ |
Dit betekent dat $2s^2 - 1$ geen priemgetal mag zijn. Hier wordt het lastiger om iets algemeens te zeggen, want we komen hier op het moeilijke terrein van de priemgetallen. Toch kun je voor oplopende $s$ zelf al snel een paar mogelijkheden vinden.
Opgave 4Voor welke laagste twee waarden van $s$ is $2s^2 - 1$ geen priemgetal? En in welke factoren $p$ (groter dan $s$) en $q$ wordt dit dan ontbonden? Bereken voor elk van deze twee waarden van $s$ de drietallen sommen van kwadraten bij $r = 0$. |
Ongelijke kwadraten
Als we algemener willen beginnen met ongelijke kwadraten, dus met $g = a^2 + b^2$ en $b \neq a$, dan wordt het iets lastiger. Toch kunnen we met onze oplossingsmethode nog een belangrijke stap maken. Zonder verdere afleiding geven we de volgende conclusie: bij elke hierboven beschreven oplossing $(a, x, y)$ met $x > 0$, voor een drietal dat begint met gelijke kwadraten, vinden we direct ook een oplossing met ongelijke kwadraten in $g$. Als $x$ oneven is en dus $y$ even wordt dat $b = ay - \tfrac{1}{2}y^2$ en
$g=a^2+b^2$
$g+1=(a-y)^2+(b+1)^2$
$g+2=(a+x)^2+(b-1)^2$
Als $x$ even is en dus $y$ oneven wordt dat $b=ax+\tfrac{1}{2}x^2 en:$
$g=a^2+b^2$
$g+1=(a+x)^2+(b-1)^2$
$g+2=(a-y)^2+(b+1)^2$
Door opeenvolgende sommen van kwadraten van elkaar af te trekken kun je dit ook zelf verifiёren. Dus ook hier oneindig veel drietallen, telkens één-op-één corresponderend met drietallen die beginnen met gelijke kwadraten.
Opgave 5Ga zelf na dat dit voor $x=2$ en $y=3$ nu het aan het begin genoemde drietal $232, 233, 234$ oplevert. |
Ten slotte
De eindconclusie is dus dat we oneindig veel drietallen opeenvolgende gehele getallen gevonden hebben die elk de som zijn van twee kwadraten. Bovendien weten we inmiddels ook dat met twee kwadraten langere rijtjes niet mogelijk zijn. Wanneer we sommen van drie kwadraten zouden bekijken, krijgen we meer mogelijkheden en zullen er wel langere rijtjes opeenvolgende getallen te vinden zijn. Dat is misschien iets voor een volgend artikel. Maar nu al kunnen we met elk gevonden drietal $g$, $g + 1$, $g + 2$ van dit artikel op de volgende triviale wijze zeventallen maken met telkens drie kwadraten in de som:
$h = g + 0^2$
$h + 1 = g + 1^2$ of $(g + 1) + 0^2$
$h + 2 = (g + 1) + 1^2$ of $(g + 2) + 0^2$
$h + 3 = (g + 2) + 1^2$
$h + 4 = g + 2^2$
$h + 5 = (g + 1) + 2^2$
$h + 6 = (g + 2) + 2^2.$
Bekijk oplossing
