Opgave 469 ^[oOO]

Omdat $x$ deelbaar is door $9$, is ook $y$, de som van de cijfers van $x$, deelbaar door $9$. Daarmee is ook $z$ deelbaar door $9$, en ook de som van de cijfers van $z$. 

Elk cijfer van $x$ is tussen de $0$ en de $9$, waarbij geldt dat minstens één van de cijfers ongelijk is aan $0$. Hieruit volgt dat $1 \le y \le 2022 \cdot 9 = 18198$. De som van de cijfers van $y$ is dan maximaal $1 + 9 + 9 + 9 + 9 = 46$, dus $1 \le z \le 46$. De som van de cijfers van $z$ is dan maximaal $3 + 9 = 12$. Echter, de som van de cijfers van $z$ is deelbaar door $9$, en het enige getal tussen de $1$ en de $12$ is $9$ zelf; dit is dus altijd de som van de cijfers van $z$.

Opgave 470 ^[oOO]

We leggen de $10 \times n$-rechthoek zo neer dat hij $10$ vakjes breed is en $n$ vakjes hoog. Het is duidelijk dat $n = 1$ en $n = 2$ beide niet mogelijk zijn. Voor $n = 3$ kijken we naar het vakje linksboven. Er zijn twee manieren om daar een tegel te leggen. In het ene geval is op de tweede rij het eerste vakje leeg en het tweede vakje
bedekt; in het andere geval zijn op de tweede rij de eerste twee vakjes leeg en is het derde vakje bedekt. In beide gevallen kan het eerste vakje in de tweede rij niet meer worden bedekt, dus $n = 3$ is ook niet mogelijk.

Voor $n = 4$ kijken we ook naar het vakje linksboven. Met hetzelfde argument voor het geval $n = 3$ hierboven kunnen we laten zien de de tegel die het vakje linksboven bedekt niet "horizontaal" kan liggen; dat wil zeggen, dat de eerste vier vakjes van de eerste rij door deze tegel worden bedekt.

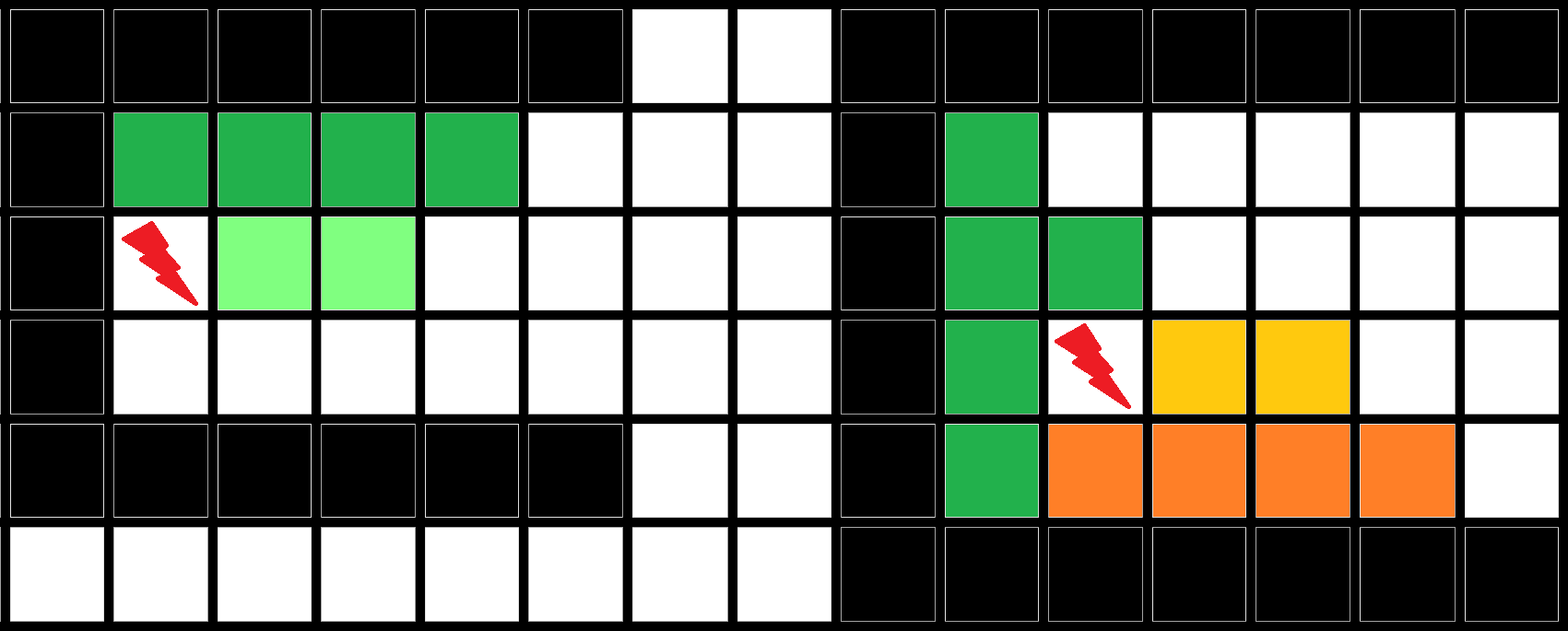
De tegel die het vakje linksboven bedekt moet dus verticaal tegen de linkerwand staan. Door eventueel te spiegelen mogen we aannemen dat het vijfde vakje van de tegel in de tweede kolom op de tweede rij ligt. Het onderste vakje in de tweede rij kan nu alleen worden bedekt met een tegel die horizontaal op de onderste rij ligt, maar in beide gevallen kan het vakje op de derde rij in de tweede kolom niet meer worden bedekt. Ook $n = 4$ is dus niet mogelijk.

Het geval $n = 5$ kan wel en daarmee is $n = 5$ de kleinste $n$ zodat de rechthoek gevuld kan worden.

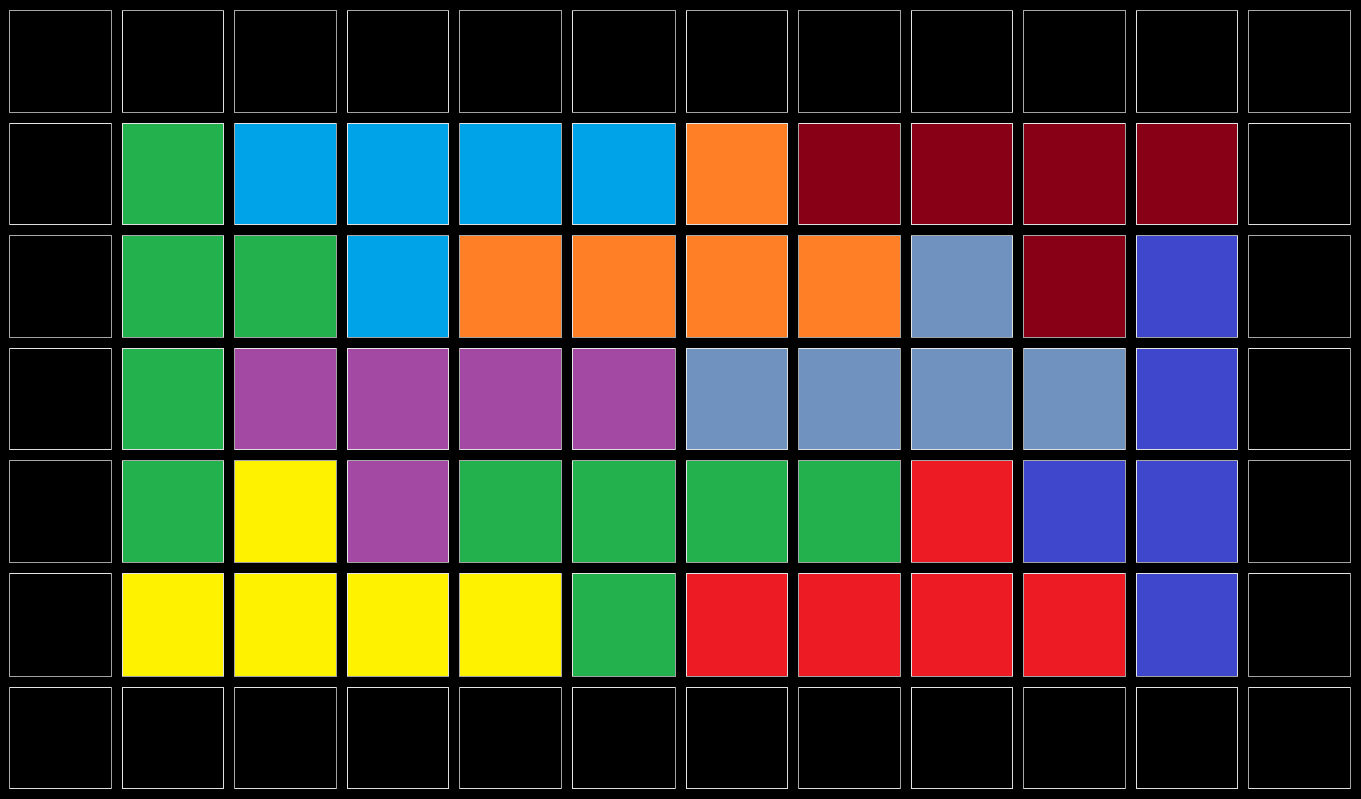
Opgave 471 ^[ooO]

Voor het eerste deel merken we op dat het altijd een diagonale stap kost om van de even naar de oneven rijen (dan wel kolommen) te gaan. In onze rondwandeling moeten we minstens één keer van de even naar de oneven rijen en minstens één keer terug. Dit betekent dat er minstens twee diagonale stappen moeten worden gezet, en dit is ook mogelijk; zie de figuur.

Voor deel twee brengen we een denkbeeldige kleuring op de sterren aan: we kleuren de kolommen van de rechthoek afwisselend blauw en rood. Zo kleuren we bijvoorbeeld de vijf sterren in de eerste kolom blauw, de vier sterren op in de tweede kolom rood, enzovoort). Elke diagonale stap brengt ons van een rode ster naar een blauwe of omgekeerd. Een rechte stap daarentegen brengt ons van rood naar rood of blauw naar blauw. Er zijn in totaal $20$ rode sterren. Een rondgang met k rechte stappen en verder diagonaal kan dus maximaal $20 + k$ blauwe sterren aandoen. Omdat er $30$ blauwe sterren zijn, zien we dat $k$ minstens tien moet zijn. Dit is ook mogelijk; zie de figuur.

Opgave 472 ^[ooO]

Het is voor Bas altijd mogelijk om de gehele rij munten met munt omhoog te krijgen, ongeacht wat Harry doet.

We maken een kleine aanpassing: we verplaatsen de munten niet meer, maar lopen we steeds door de rij munten heen, van links naar rechts. (Overtuig jezelf ervan dat dit hetzelfde spel is.) We geven de munten ook een waarde: we geven de meest linker munt waarde $0$ als munt boven ligt en waarde $1$ als kop boven ligt. De tweede munt geven we waarde $0$ als munt boven ligt en waarde $2$ als kop boven ligt. De derde munt geven we waarde $0$ als munt boven ligt en waarde $4$ als kop boven ligt. Dit doen we ook met de overige munten (de laatste munt heeft waarde $0$ of $32$). De score van een hele rij is de som van de waarden van de individuele munten: de waarde van de rij ligt dus altijd tussen $0$ (alle munten liggen met munt omhoog) en $1+2+4+8+16+32 = 63$ (alle munten liggen met kop omhoog).

Het doel van het spel is om alle munten met munt omhoog te krijgen, oftewel score $0$. Om dit te bereiken is echter ook score $63$ goed: dan ligt de hele rij met kop omhoog, dus mag Bas al deze munten achter elkaar in munt veranderen, en wint hij daarmee het spel. We hebben dus twee mogelijke doelen: de score zo laag als mogelijk krijgen, of de score zo hoog als mogelijk.

Stel dat we ons in de situatie bevinden dat de munt helemaal links aan de beurt is. We bekijken de volgende zes beurten, dat wil zeggen, totdat de hele rij munten een keer aan de beurt is geweest. Bas kan nu de volgende strategie toepassen: hij draait elke munt die met kop naar boven ligt om, zodat deze nu met munt naar boven ligt. Harry moet hierop reageren: als hij alle munten met munt naar boven zo laat liggen, dan zal aan het eind van deze zes beurten de gehele rij munt zijn en dan wint Bas. Dit betekent dat Harry een munt die met munt omhoog ligt naar kop zal draaien. Bas past vanaf dat moment zijn strategie aan: hij laat nu alle munten met kop naar boven zo liggen (totdat de zes beurten afgelopen zijn).

We laten met een voorbeeld zien dat de score van de rij na deze zes beurten altijd is gestegen. Dit is daarmee een winnende strategie voor Bas: omdat de score altijd zal stijgen, komen we op een gegeven moment op score $63$ uit, oftewel een rij met alleen maar kop. Bas kan nu alles naar munt draaien. Stel dat Bas de eerste vier munten van kop naar munt heeft gedraaid, waarna Harry de vijfde munt van munt naar kop draait. De eerste vier zetten halen $1 + 2 + 4 + 8 = 15$ van de score van de rij af, waarna de vijfde zet juist $16$ toevoegt. Met Bas zijn strategie zal de score van de rij zes zetten later dus hoger zijn, waaruit volgt dat Bas altijd kan winnen.