Oplossing 358 [niveau oOO]

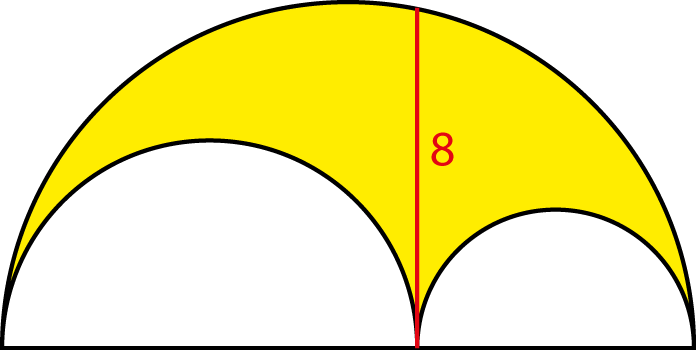
Hieronder zijn drie halve cirkels getekend. Het rode lijnstuk heeft lengte 8 en raakt beide kleine halve cirkels. Bepaal de oppervlakte van het gele gedeelte.

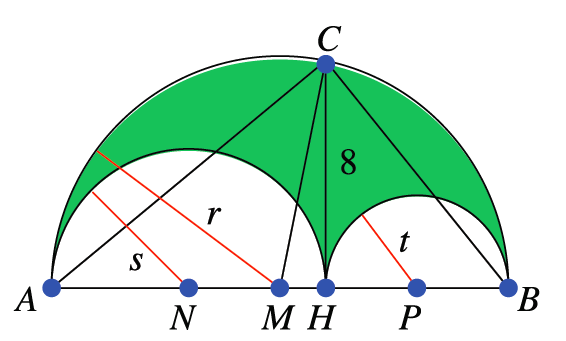Oplossing. We tekenen een aantal punten in de figuur: $A$ en $B$ zijn de uiteinden van de middellijn, $C$ en $H$ zijn de uiteinden van het gegeven verticale lijnstuk. $M$ is het middelpunt van de groene cirkel, met straal $r$. De cirkelboog aan de linkerzijde heeft middelpunt $N$ en straal $s$. De cirkelboog aan de rechterzijde heeft middelpunt $P$ en straal $t$. Eenvoudig valt af te leiden dat $r = s + t$ en dat $MH = 2s – r = s – t$. Voor de
rechthoekige driehoek $MHC$ geldt volgens Pytha­goras dat $r^2 = 64 + (s – t)^2$, ofwel $4st =64$. Het gewenste oppervlak is ${1 \over 2} \pi (r^2 − s^2 − t^2 ) = \pi st = 16\pi$.

 

Oplossing 359 [niveau oOO]

Een archipel bestaat uit $64$ eilanden. Elk eiland is voorzien van een haven. In elke haven staan $63$ containers gereed, bestemd voor de $63$ andere eilanden. Je wilt met één schip alle vracht in de havens van bestemming brengen. Je vertrekt vanaf eiland $1$, vaart via de eilanden $2$ tot en met $63$ (die je elk precies één keer aandoet) naar eiland $64$, en vaart vervolgens in omgekeerde richting weer terug naar eiland $1$ (waarbij je opnieuw de eilanden $63$ tot en met $2$ elk één keer aandoet). Hoeveel containers moeten er minimaal op het schip passen?
Oplossing. We nummeren de eilanden (havens) van $1$ t/m $64$, waarbij Haven $1$ de vertrekhaven is en Haven $64$ de haven is waar omgedraaid wordt, waarna de terugreis begint. Voor elke container geldt dat deze wordt vervoerd van $K$ naar $L$, waarbij $K \neq L$. Als $K < L$ dan moet deze op de heenreis meegenomen worden. Als $K > L$, dan kun je in principe kiezen voor zowel meenemen op de heen als terugreis, maar handig is om de container op de terugreis pas in te laden. Als de boot vaart van haven $K$ naar haven $K + 1$ dan zijn er op de boot containers afkomstig van de eilanden $1$ t/m $K$, die zijn bestemd voor $K+1$ t/m $64$. Aangezien voor elke combinatie van twee eilanden een aparte container op het dek staat, gaat het dus om $K(64 – K) = 64K – K^2$ containers. Het maximum wordt aangenomen voor $K = 32$, immers $64K – K^2 = 1024 – (K – 32)^2 ≤ 1024$. Tussen Haven $32$ en Haven $33$ vaart de boot met $1024$ containers. Op de terugweg gebeurt identiek hetzelfde en vaart de boot tussen Haven $33$ en Haven $32$ opnieuw met $1024$ containers.

 

Oplossing 360 [niveau ooO]

Jelly houdt al haar hele leven bij wanneer ze op dezelfde weekdag jarig is als haar geboortedag. De eerste keer is ze vergeten, maar de tweede keer was op haar 11de verjaardag en de derde keer op haar 22ste verjaardag. Hoe oud werd ze op haar verjaardag toen deze voor de eerste keer op dezelfde weekdag viel als haar geboortedag?
Oplossing. In de schrikkeljaren schuift de dag van de week 2 dagen op, in een “gewoon” jaar is dat slechts een dag. We onderscheiden vier gevallen:

1. Jelly is geboren in een schrikkeljaar (voor ons gemak laten we dit lopen van 1 maart tot en met 28 februari)
2. Jelly is geboren in het jaar na een schrikkeljaar
3. Jelly is geboren in het tweede jaar na een schrikkeljaar
4. Jelly is geboren in het jaar voor een schrikkeljaar

De dag waarop haar geboorte viel geven we aan met 0. De dag erna met 1, dan, 2, 3, 4, 5 en 6. Daarna weer 0. Het maakt niets uit welke dag we met de 0 aangeven. Met de getallen 0 t/m 6 noteren we op welke dag de verjaardag van Jelly valt op de opeenvolgende jaren (zie onderstaande figuur).

Met een 0 wordt aangegeven dat de dag dezelfde is als haar geboortedag. Er zijn twee mogelijkheden met zowel bij de 11de als de 22ste verjaardag een 0. Die in regel 3 valt af, want we zochten de eerste verjaardag. De verjaardag die ze is vergeten staat dus in regel 4: haar vijfde verjaardag. De verjaardag die ze vergeten is, is haar vijfde verjaardag.

 

Oplossing 361 [niveau ooO]

Bepaal alle viertallen reële getallen $a$, $b$, $c$, $d$ die voldoen aan
\(\begin{eqnarray} a + c &=& –5\qquad(1)\\ b + d + ac &=& 5\;\;\,\qquad(2)\\ ad + bc &=& 5\;\;\,\qquad(3)\\ bd &=& –6 \qquad(4) \end{eqnarray}\)
Oplossing. Tel de $4$ vergelijkingen bij elkaar op. We krijgen nu: $a + b + c + d + ac + ad + bc + bd = –1$ ofwel $(a + b)(c + d) + a + b + c + d + 1 = 0$. Nu volgt de ontbinding in twee factoren: $(a + b + 1)(c + d + 1) = 0$. Dat betekent dat ofwel $a + b = –1$ ofwel $c + d = –1$. Nu nemen we vergelijking $(1)$ minus vergelijking $(2)$ plus vergelijking $(3)$ minus vergelijking $(4)$. We hebben nu $a – b + c – d – ac + ad + bc – bd = 1$. Ofwel $(a – b)(d – c) + a – b + c – d – 1 = 0$. Ook nu kunnen we ontbinden in twee factoren: $(a – b – 1)(d – c + 1) = 0$. Dit betekent ofwel $a – b = 1$ ofwel $c – d = 1$. We moeten nu $4$ mogelijkheden bekijken:

1. $a + b = –1$ en $a – b = 1$. Eenvoudig volgt $a = 0$ en $b = –1$. Uit vergelijking $(1)$ volgt $c = –5$. Ten slotte volgt uit vergelijking $(2)$ dat $d = 6$.
2. $a + b = –1$ en $c – d = 1$. We substitueren $b = –a – 1$ en $c = d + 1$ in vergelijking $(3)$. We vinden $ad + (–a –1)(d + 1) = 5$ ofwel $–a – d – 1 = 5$. We kunnen nu $a$, $b$ en $c$ uitdrukken in $d$ als volgt: $a = – d – 6$, $b = –a – 1 = d + 5$ en $c = d + 1$. We substitueren $b$ in vergelijking $(4)$: $(d + 5)d = –6$ ofwel $d^2 + 5d + 6 = 0$. Ontbind het linkerlid in factoren: $(d + 2)(d + 3) = 0$. Hieruit volgen twee waarden voor $d$, namelijk $d = –2$ en $d = –3$. De bijbehorende oplossingen voor $(a, b, c, d)$ zijn $(–4, 3, –1, –2)$ en $(–3, 2, –2, –3)$.
3. $c + d = –1$ en $a – b = 1$, ofwel $c = –d – 1$ en $b = a – 1$. Uit vergelijking $(1)$ volgt $a = –c – 5$. We kunnen nu $a$, $b$ en $c$ uitdrukken in $d$ als volgt: $a = –c – 5 = d – 4$, $b = a – 1 = d – 5$ en $c = –d – 1$. We substitueren $b$ in vergelijking $(4)$: $(d – 5)d = –6$ ofwel $d^2 – 5d + 6 = 0$. Ontbind het linkerlid weer in factoren: $(d – 2)(d – 3) = 0$. Hieruit volgen twee waarden voor $d$, namelijk $d = 2$ en $d = 3$. De bijbehorende oplossingen voor $(a, b, c, d)$ zijn $(–2, –3, –3, 2)$ en $(–3, 2, –4, 3)$.
4. $c + d = –1$ en $c – d = 1$. Nu volgt eenvoudig dat $c = 0$ en $d = –1$. Uit vergelijking $(1)$ volgt dat $a = –5$ en uit $(4)$ volgt $b = 6$.

Nu nemen we alle oplossingen samen: $$(a, b, c, d) \in \{(0, –1, –5, 6),
(–4, 3, –1, –2), (–3, 2, –2, –3), (–2, –3, –3, 2), (–3, 2, –4, 3), (–5, 6, 0, –1)\}$$