Opgave 393 [oOO]

Je komt in een hotel terecht met drie dames (Karin, Lieke en Maaike). Je weet dat elk van deze dames of de waarheid spreekt of liegt. Een dame die liegt, doet dat consequent, dat wil zeggen: élke afzonderlijke bewering is gelogen. Het hotel heeft 10 kamers, genummerd van 1 t/m 10. De dames doen over deze kamers de volgende uitspraken:

• Karin : kamer 1 is vrij, kamer 3 is bezet, kamer 4 is bezet, kamer 5 is vrij, kamer 8 is bezet.
• Lieke: kamer 2 is bezet, kamer 4 is vrij, kamer 10 is vrij.
• Maaike: kamer 6 is vrij, kamer 7 is bezet, kamer 9 is bezet, kamer 10 is vrij.

Hoeveel kamers zijn er minimaal vrij en hoeveel kamers zijn er minimaal bezet?

Oplossing. We weten vooraf niet wie er liegt en wie er de waarheid spreekt. Maar we weten wel dat een kamer of bezet is of vrij. Zo kunnen de uitspraken van Karin en Lieke nooit gelijktijdig waar zijn, want dan is gelijktijdig kamer 4 bezet en vrij. We veronderstellen daarom dat Karin liegt. We zien ook een relatie tussen de uitspraken van Lieke en Maaike, aangaande kamer 10.

We stellen nu een tabel op voor de uitspraken van de drie dames. We geven met "-" aan dat de betreffende dame geen uitspraak doet. Met "0" zegt de dame dat de kamer vrij is en met "1" zegt de dame dat de kamer bezet is.

	1	2	3	4	5	6	7	8	9	10
Karin	1	-	0	0	1	-	-	0	-	-
Lieke	-	1	-	0	-	-	-	-	-	0
Maaike	-	-	-	-	-	0	1	-	1	0
Totaal	1	1	0	0	1	0	1	0	1	0

Als Karin liegt en Lieke en Maaike spreken de waarheid, dan zijn er 5 kamers bezet en zijn er 5 kamers vrij. Als omgekeerd Karin de waarheid spreekt, dan moeten Lieke en Maaike allebei liegen (vanwege de gekoppelde uitspraken voor kamer 4 en kamer 10). In dat geval zullen alle vrije kamers bezet zijn en alle bezette kamers vrij. Ook dan zijn 5 kamers vrij en 5 kamers bezet.

Opgave 394 [oOO]

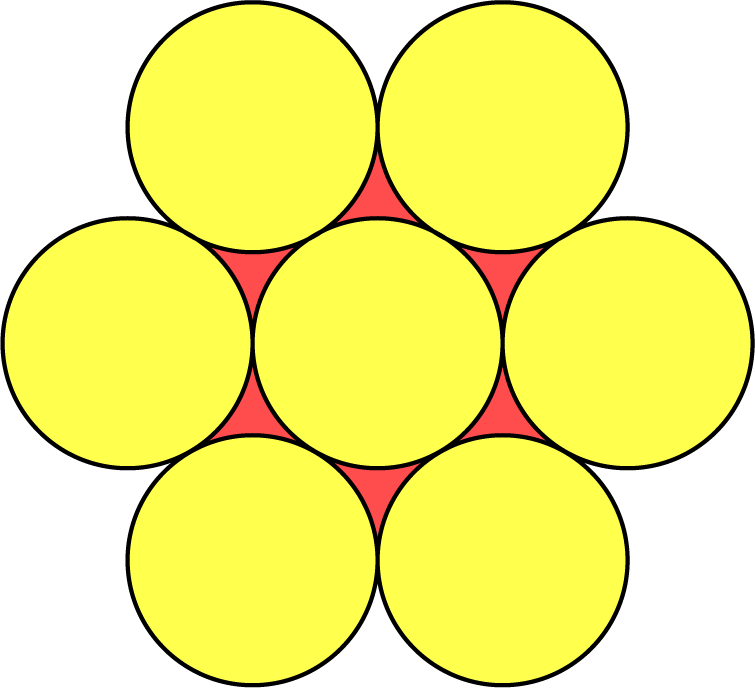
Deze figuur wordt begrensd door 6 gelijke cirkeldelen. Elk cirkeldeel heeft straal $2.$ De figuur is 6-voudig draaisymmetrisch en de cirkeldelen raken elkaar.

Wat is de oppervlakte van deze figuur?

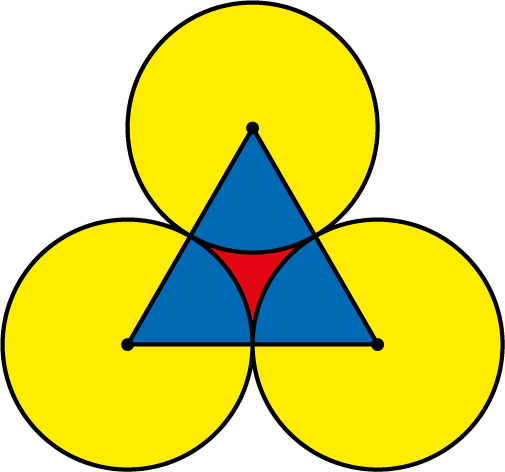
Oplossing. We tekenen de volledige cirkels. De te berekenen oppervlakte bestaat uit de oppervlakte van $7$ gele cirkels en $6$ rode driehoekig gekromde oppervlakten. De oppervlakte van een cirkel is $\pi 2^2 = 4\pi$. Om de oppervlakte te bepalen kijken we naar de andere figuur. We zien daar dat de oppervlakte van het rode oppervlak gelijk is aan de oppervlakte van een gelijkzijdige driehoek met zijde $4$ minus $3$ blauwe segmenten van $60^{\circ} (\frac{1}{6}$ van de cirkel). Ofwel het rode oppervlak is $2 \cdot 2\sqrt{3} - \frac{3}{6}\cdot 4\pi = 4\sqrt3 - 2\pi$. Daarmee is de totale oppervlakte $7\cdot 4\pi +6\cdot(4\sqrt3 - 2\pi) = 24\sqrt{3} + 16\pi.$

Opgave 395 [ooO]

Gegeven een piramide met een vierkant grondoppervlak met zijde $10$ en hoogte $15.$ Bepaal de grootst mogelijke kubus die in deze pyramide kan worden geplaatst.

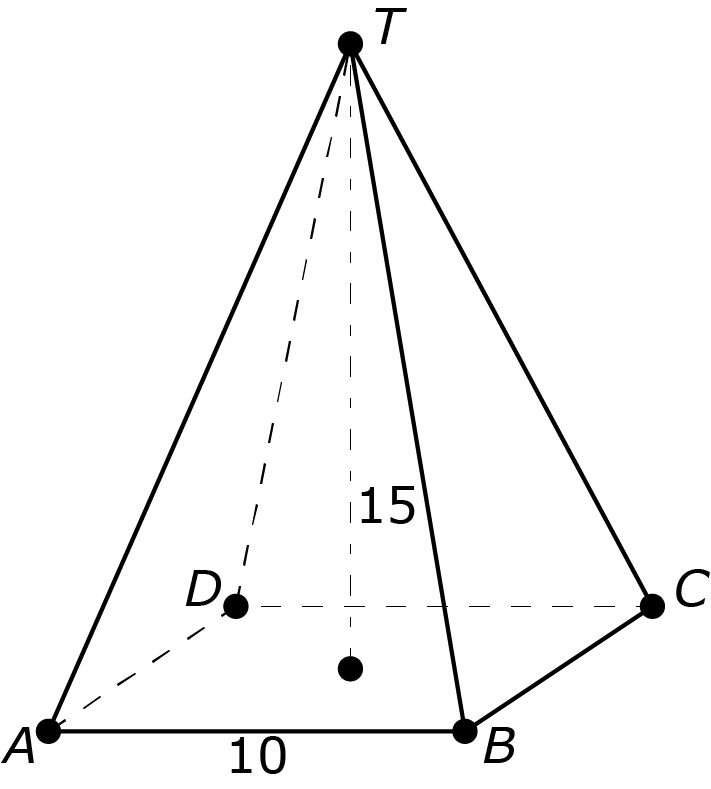
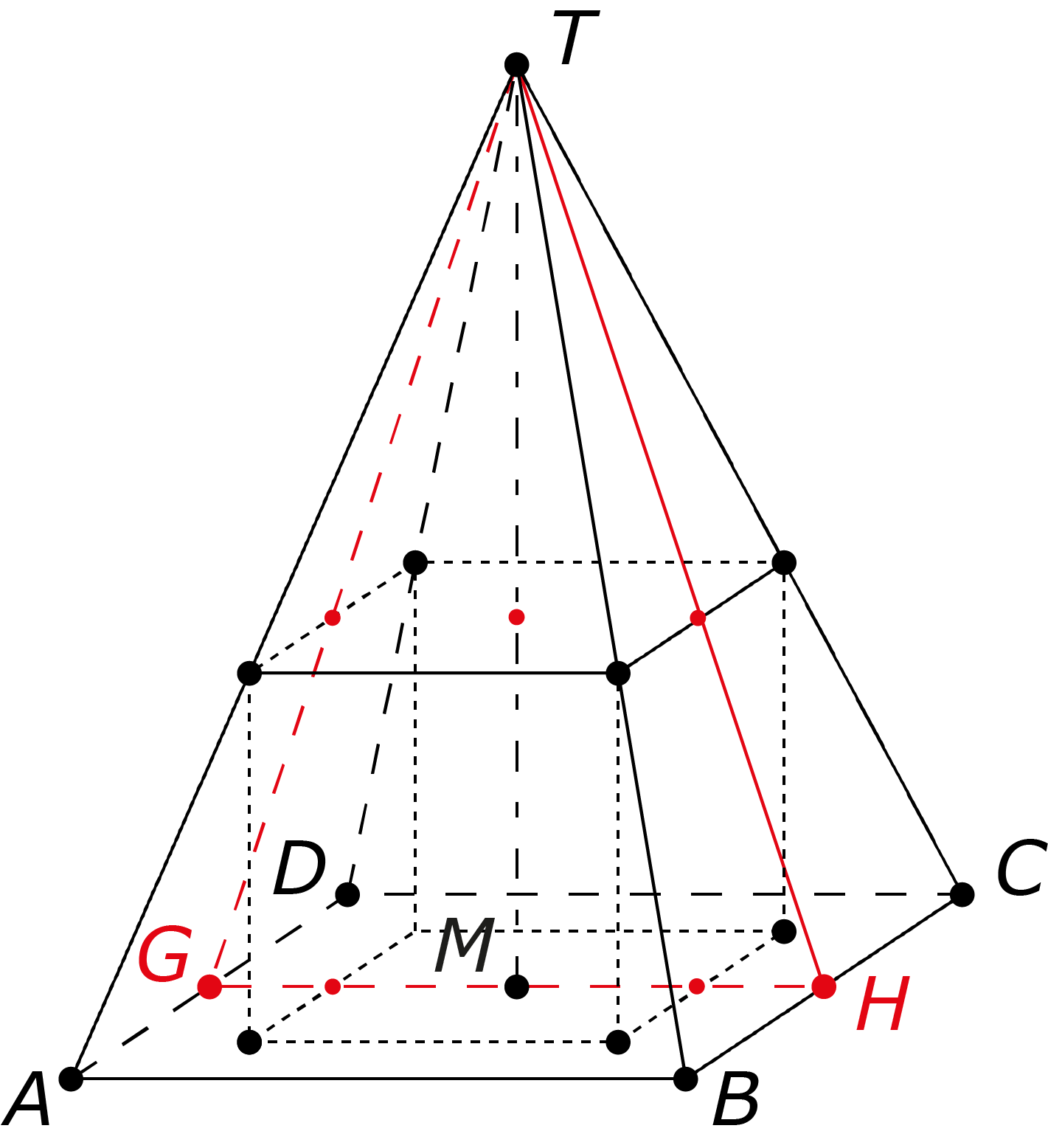
Oplossing. We hebben de kubus geplaatst in de piramide, zoals die geplaatst moet worden. De rode lijnen in de figuur links vormen een vlak dat de piramide loodrecht op het grondvlak snijdt door $T$ en evenwijdig aan het lijnstuk $AB.$ Vervolgens bekijken we deze doorsnede. Zie de volgende figuur.

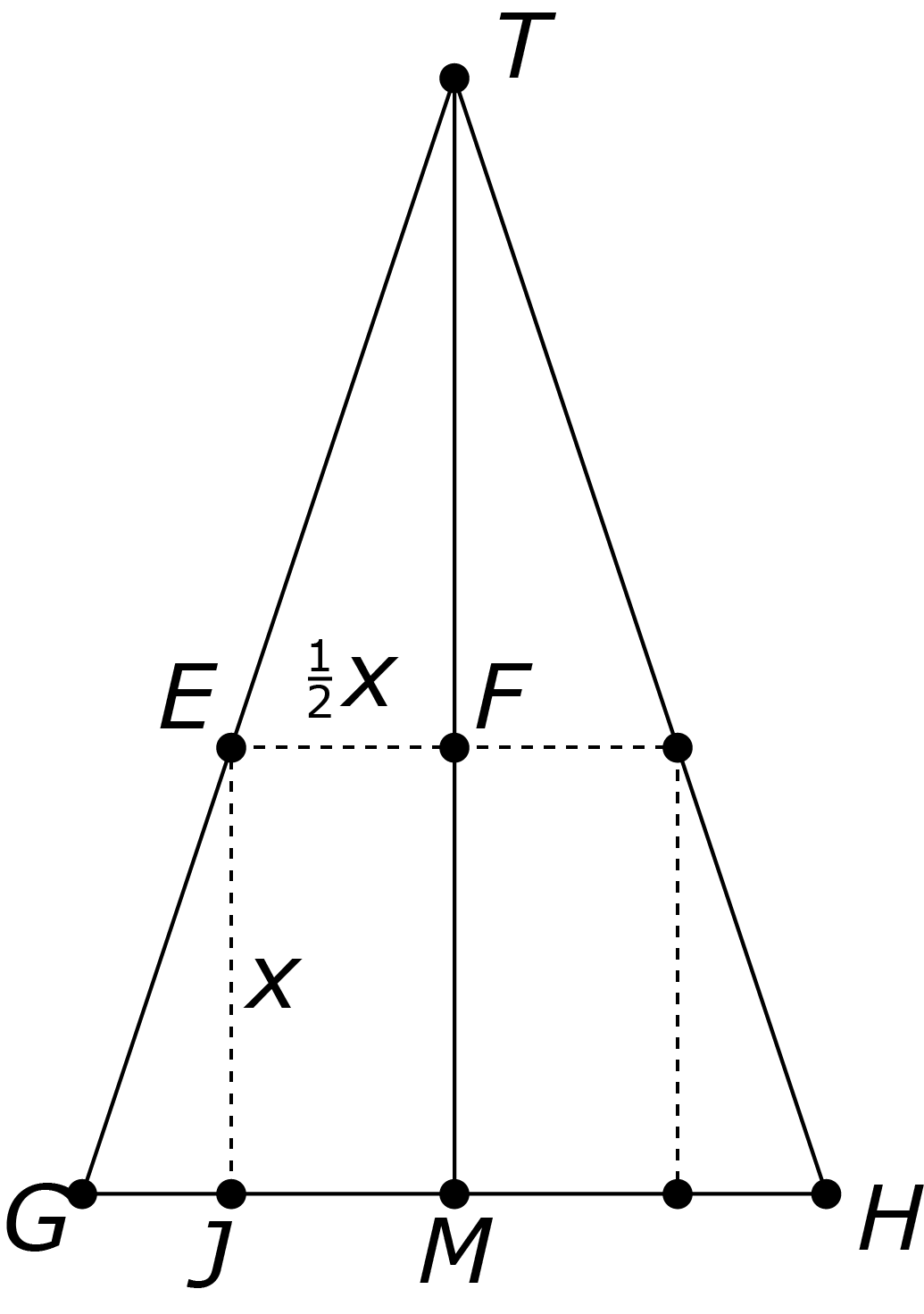De zijde van het vierkant noemen we $x.$ Zij $M$ het midden van $GH, J$ het hoekpunt van het vierkant dat op lijnstuk $GM$ ligt en $E$ het punt waar het vierkant zijde $GT$ raakt. Dan is $|JM|=\frac{1}{2}x,$ dus is $|GJ|=5-\frac{1}{2}x.$ Bovendien is $|JE|=x.$ Omdat $JE\parallel MT,$ is $\triangle GJE\sim\triangle GMT,$ dus vinden we $|GJ|:|JE|=|GM|:|MT|,$ ofwel $\frac{5-\frac{1}{2}x}x=\frac{5}{15}.$ Vermenigvuldigen met $6x$ geeft ons: $30 - 3x = 2x,$ ofwel $30 = 5x,$ dus is $x = 6.$

Opgave 396 [ooO]

Patrick heeft tien verschillende, strikt positieve getallen. Hij telt ze alle tien bij elkaar op tot het getal $A.$ Ook neemt hij $1$ gedeeld door elk van deze getallen en telt deze tien nieuwe getallen op tot het getal $B.$ Tenslotte berekent hij het product $A \cdot B.$ Kan dit getal kleiner zijn dan $55?$ Waarom wel of niet?

Oplossing. We veronderstellen dat de 10 getallen $a_1 < a_2 < a_3 < \cdots < a_{10}$ zijn. Nu is $A = a_1 + a_2 + a_3 + \cdots + a_{10}$ en $B = \frac{1}{a_1} + \frac{1}{a_2} + \frac{1}{a_3} + \cdots + \frac{1}{a_{10}}.$ Voor het product $AB$ geldt dat dit de som is van 100 termen, alle van de vorm $\frac{a_i}{a_j}$. Als $i < j$ dan is dit quotiënt kleiner dan $1,$ en dan negeren we dit. Als echter $i \ge j$ dan is het quotiënt groter of gelijk aan $1.$ Het aantal keren dat $i \ge j$ is $1 + 2 + 3 + \cdots + 10 = 55.$ De som is dus altijd strikt groter dan $55.$

Nogmaals opgave 387

Vind alle gehele getallen $n$ waarvoor geldt:

$$\max(2n - 11 + 2n^6, 2\max(n - 7 + n^6, 5 - 2n + 6n^6)) \le 2n^6.$$

Hierbij staat $\max(a, b)$ voor het maximum, dus de grootste, van de getallen $a$ en $b.$ Bijvoorbeeld, $\max(3, 5) = 5, \max(-3, -5) = -3$ en $\max(3, 3) = 3.$

De redactie had de indruk dat opgave 387 uit Pythagoras 58-1 exact identiek was aan opgave 381 uit Pythagoras 57-5/6. Dat bleek onjuist. Door een klein verschil is de uitwerking anders. De redactie beoordeelde dat de opgave daarom apart meetelt.