In 1643 stelde Fermat aan Torricelli de vraag om bij een gegeven driehoek het punt te construeren waarvoor de som van de afstanden tot de 3 hoekpunten zo klein mogelijk is. Hij loste het op en sindsdien heet dit punt het punt van Torricelli. In de negende en de achtenveertigste jaargang van Pythagoras staan mooie bewijzen van de constructie.

Er zijn twee gevallen. Als de hoek van een in de hoekpunten groter is dan of gelijk aan $120^{\circ},$ dan is dat hoekpunt het punt van Torricelli.

Als alle hoeken van de driehoek kleiner zijn dan $120^{\circ},$ dan construeer je het punt zoals in de volgende figuur.

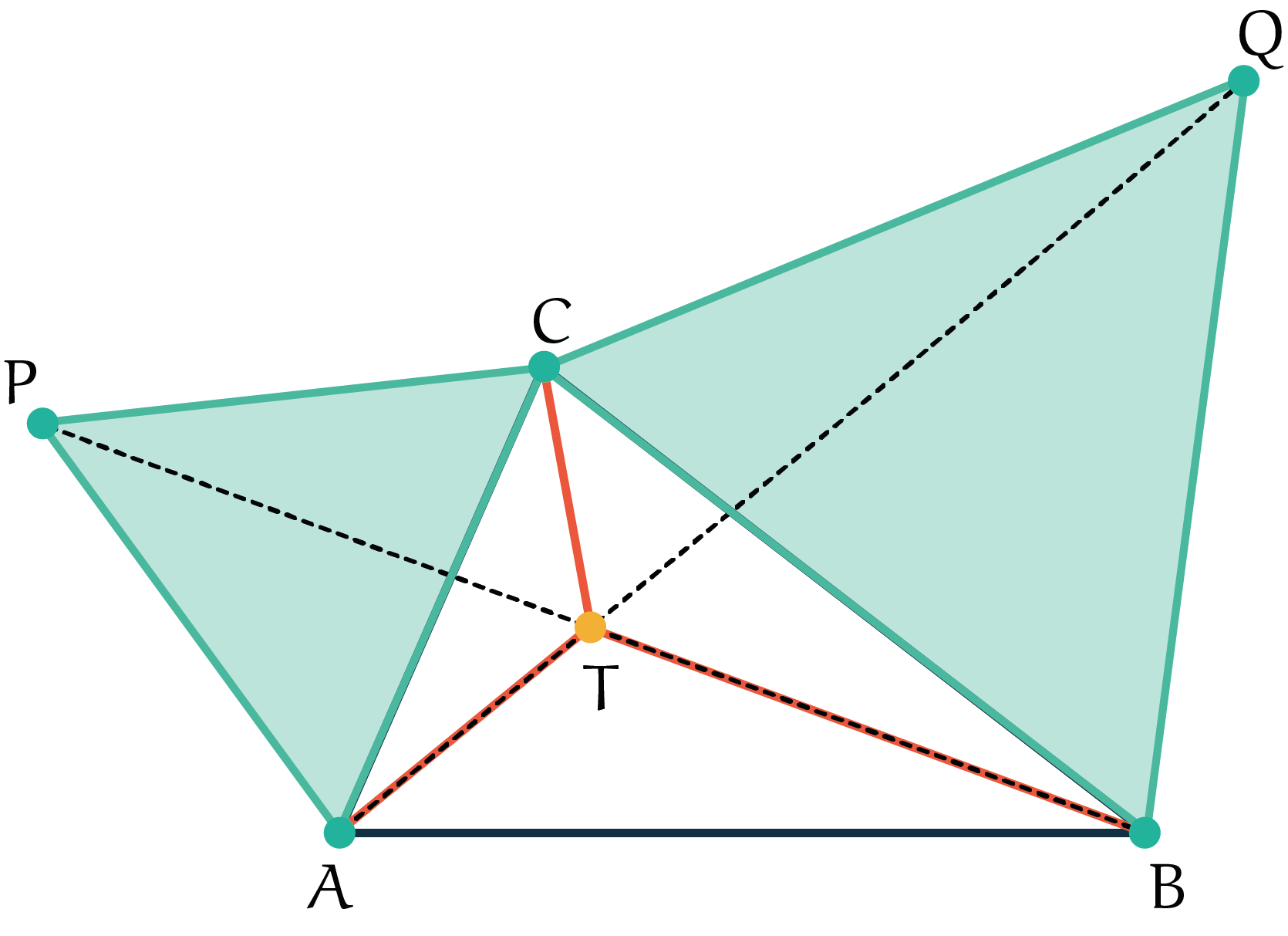
Teken op de zijden $AC$ en $BC$ gelijkzijdige driehoeken $\Delta ACP$ en $\Delta BCQ.$ Het snijpunt $T$ van de rechten $AQ$ en $BP$ is het gewenste punt. Uit de constructie van het punt $T$ kan worden afgeleid dat de hoeken $\angle ATC$ en $\angle ATB$ gelijk zijn aan $120^{\circ}.$

In 1836, in een brief aan de astronoom Christian Schumacher, tekende Gauss verschillende voorbeelden van het kortste netwerk tussen vier punten. In de figuur hieronder staan twee gevallen. De grijze punten zijn gegeven, de groene punten zijn Torricellipunten.

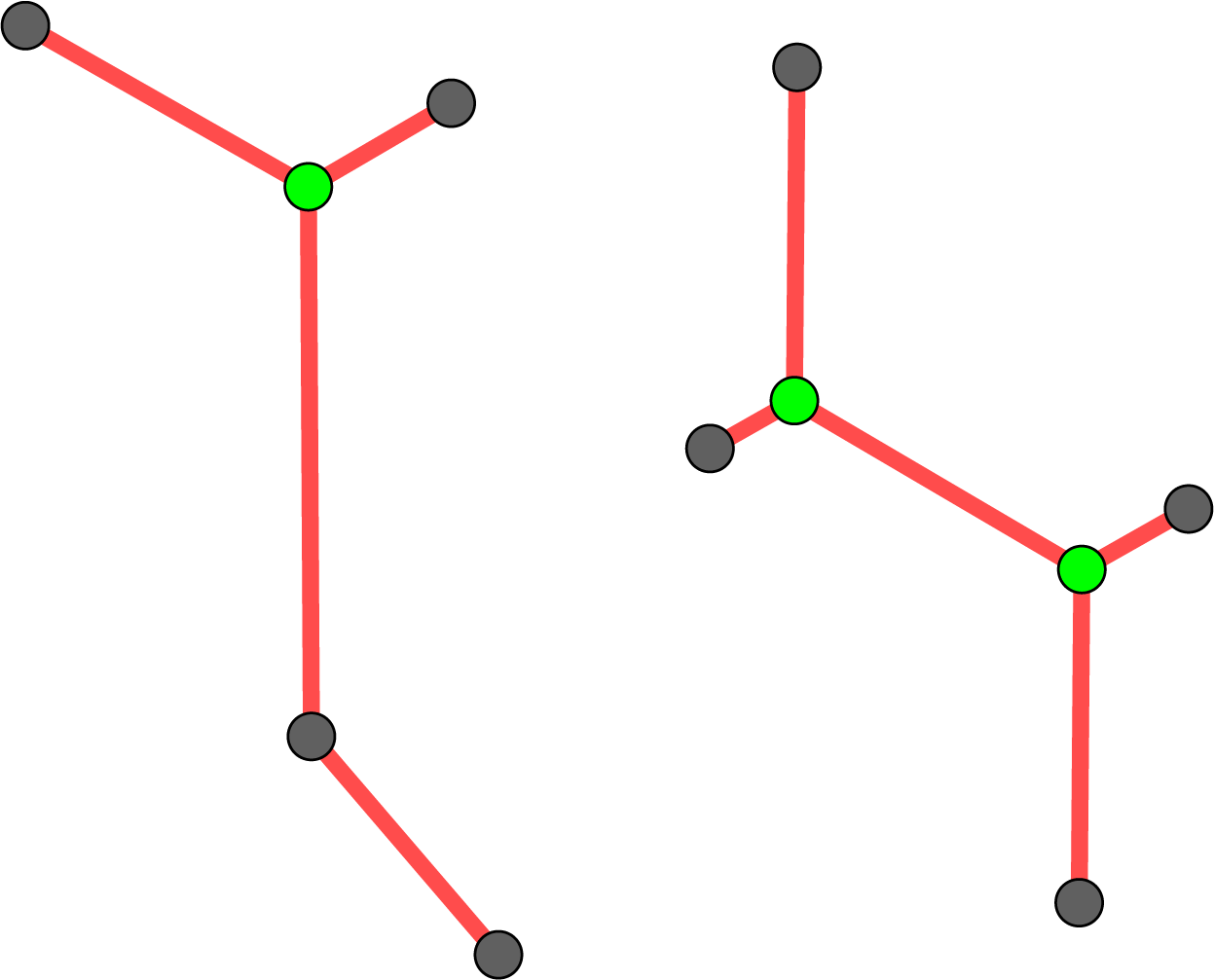
Het is interessant dat we voor het kortste netwerk tussen vier punten in het algemeen twee Torricellipunten moeten introduceren. De hoeken bij deze punten zijn $120^{\circ}.$ De algemene constructie staat in de volgende figuur en gaat weer met gelijkzijdige driehoeken.

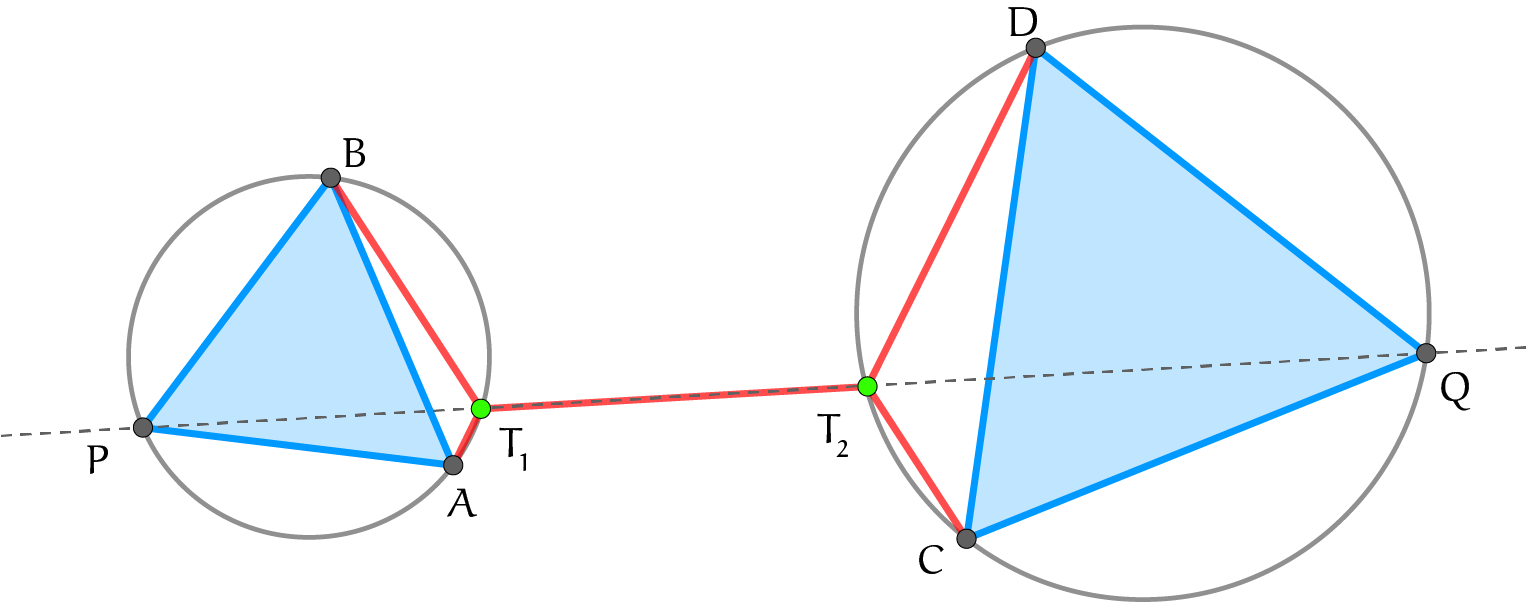
Dezelfde vraag voor een willekeurig aantal punten kan wel worden opgelost, maar er zijn steeds meer Torricellipunten nodig. Het aantal mogelijkheden voor het plaatsen van deze punten neemt zeer snel toe en het probleem wordt snel praktisch onoplosbaar.

 

Feuerbach | Poncelet | Pascal | Morley | Torricelli | Ceva