Opgave 553 ^[oOO]

Merk eerst op dat er in totaal $12$ verschillende letters in de woorden voorkomen. Daarom komt elke letter op precies één zijde van één dobbelsteen voor. Door het woord $DOR$ weten we dat $D$, $O$ en $R$ elk op verschillende dobbelstenen voorkomen. We noteren dit als

$\{D\}, \{O\}, \{R\}$.

Het woord $RED$ leert ons dat $E$ niet op dezelfde dobbelsteen als $R$ of $D$ staat, en dus op die van $O$ moet staan. We schrijven

$\{D\}, \{O,E\}, \{R\}$,

waarbij $\{O,E\}$ dus aangeeft dat $O$ en $E$ op dezelfde dobbelsteen staan. Op dezelfde manier leren we van $IER$ dat we hebben 

$\{D, I\}, \{O,E\}, \{R\}$.

Uit $RIT# krijgen we

$\{D, I\}, \{O,E,T\}, \{R\}$.

Door het woord $DAL$ weten we dat de $A$ niet in $\{D, I\}$ zit, en door $GAT$ weten we dat de $A$ niet in $\{O,E,T\}$ hoort. Dus hebben we 

$\{D, I\}, \{O,E,T\}, \{R, A\}$.

Nu kunnen we de overige letters van $DAL$ en $GAT$ ook een plekje geven:

$\{D, I,G\}, \{O,E,T, L\}, \{R, A\}$.

Nu moeten we alleen de letters $N$, $S$ en $V$ nog verdelen. Door de woorden $ONS$ en $VEN$ weten we dat de $N$ niet bij de $S$ en niet bij de $V$ kan. De enige optie is dus 

$\{D, I, G, N\}, \{O,E,T, L\}, \{R, A, S, V\}$.

Tot slot is het gemakkelijk te zien dat alle woorden inderdaad te vormen zijn met deze drie dobbelstenen.

Opgave 554 ^[oOO]

We noteren het cijfer dat op de eerste plaats staat als $n_0$, wat dus ook het totaal aantal nullen weergeeft. Het cijfer op de tweede plaats geven we weer met $n_1$, wat gelijk is aan het aantal éénen, enzovoorts. Merk eerst op dat het totaal aantal cijfers gelijk is aan de som van $n_0$ tot en met $n_9$, waaruit volgt dat

$n_0 + n_1 + \dots + n_9 = 10$.

We kijken eerst naar de waarde van $n_0$. Hieruit volgt dat er precies $10-n_0$ cijfers ongelijk aan $0$ zijn, wat betekent dat het totaal aantal verschillende cijfers in het getal gelijk is aan $10-n_0$. Als we er hier $6$ of meer van hebben, dan is de som van deze cijfers minstens gelijk aan $0+1+2+3+4+5 = 15 > 10$. Dit kan niet, en dus concluderen we dat $10-n_0 \le 5$, waaruit volgt dat $n0 \ge 5$. De situatie $n_0 = 5$ kunnen we ook gemakkelijk uitsluiten. In dat geval komen er $5$ verschillende cijfers voor in het getal, waarvan één gelijk is aan $5$. Echter, nu is de totale som al minstens $0 + 1 + 2 + 3 + 5 = 11$. We concluderen dat

$n_0 \ge 6$.

Vervolgens kijken we naar de waarden $n_6$ tot en met $n_9$. Doordat $n_0 \ge 6$, komt minstens één van de getallen $6$ tot en met $9$ een keer voor. Bovendien kan een getal boven de $5$ niet twee keer voorkomen, en kunnen we ook niet twee van deze getallen hebben, aangezien in beide gevallen de som van de cijfers boven de $10$ uitkomt. We concluderen dat precies één van de getallen $n_6, \dots, n_9 \ge 1$ gelijk is aan $1$, terwijl de andere $0$ zijn. We kunnen dit kort weergeven als

$n_6 + \dots + n_9 = 1$.

Uit bovenstaande zien we ook dat $n_1 \ge 1$. Bovendien is $n_1 = 1$ niet mogelijk, aangezien we dan tweemaal een $1$ zouden hebben (namelijk voor $n_1$ en voor $n_6, n_7, n_8$ of $n_9$). We vinden dus

$n_1 \ge 2$.

Samenvattend hebben we dus al

$n_0 + n_1 + (n_6 + \dots + n_9) \ge 6 + 2 + 1 = 9$

zodat

$n_2 + \dots + n_5 \le 1$.

Doordat $n_2 \ge 2$, moeten we nog minstens één $1$ kwijt, wat alleen op $n_2$ tot en met $n_5$ kan. Uit $n_2 + \dots + n_5 \le 1$ volgt dat dit precies één $1$ is, zodat $n_1 = 2$. Nu weten we ook waar deze laatste $1$ naartoe moet; kennelijk hebben we $n_2 = 1$, aangezien een $2$ voorkomt. Tot slot kunnen we alleen een som van $10$ krijgen als $n_0 = 6$, waaruit volgt dat $n_6 = 1$. Het enige getal dat kan voldoen is dus

$6\,210\,001\,000$.

We kunnen gemakkelijk controleren dat dit getal ook inderdaad werkt.

Opgave 555 ^[ooO]

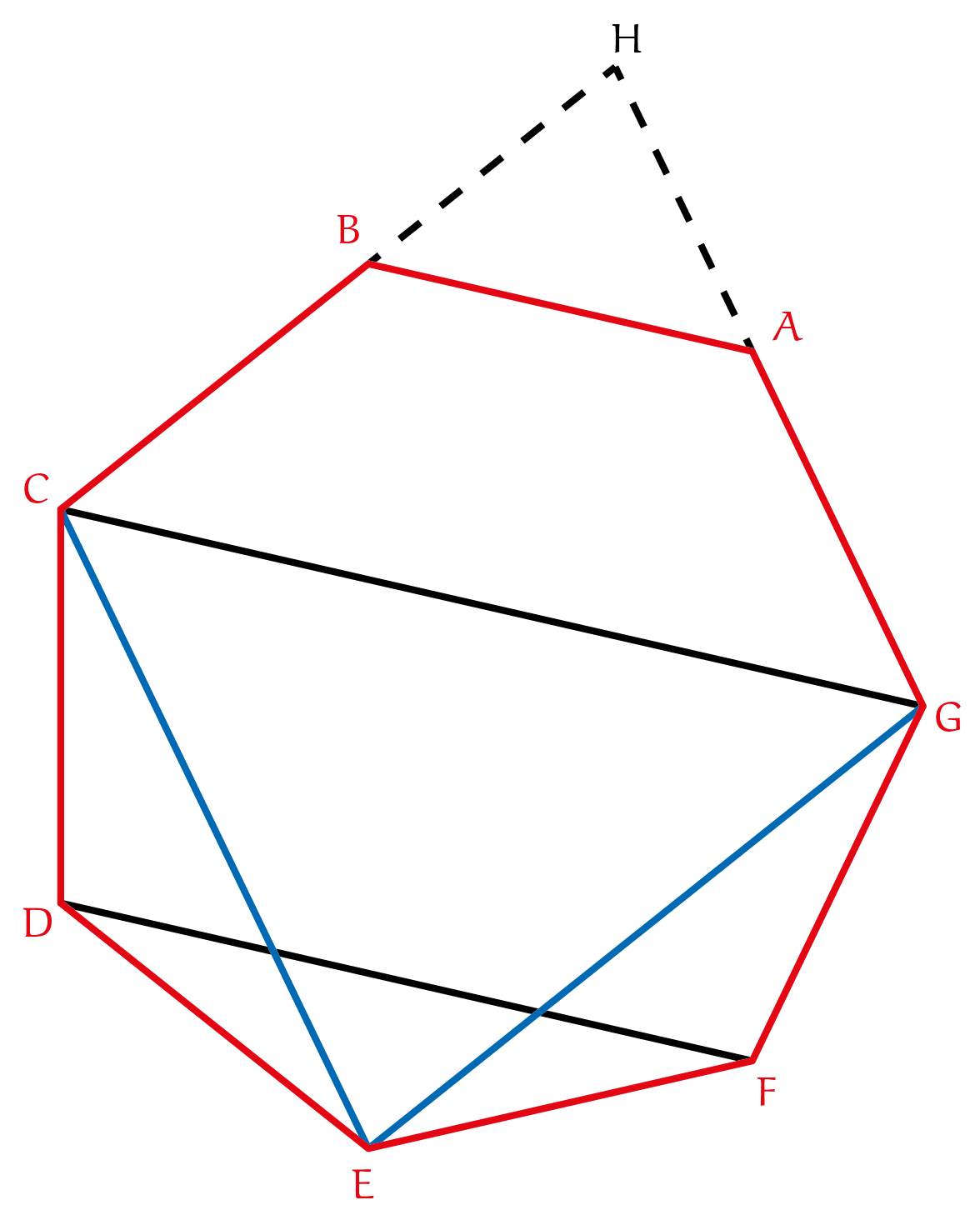
We tekenen de lijnstukken $CE$ en $EG$; zie de figuur. Merk op dat door symmetrie de driehoeken $GHC$ en $GEC$ allebei gelijkbenig zijn, met $GH = CH$ en $EG = CE$. Bovendien hebben deze twee driehoeken de zijde $CG$ gemeen. Als we kunnen aantonen dat $\angle\text{EGC} = \angle\text{HGC}$, dan zijn de twee driehoeken gelijk, waaruit volgt dat $H$ inderdaad het spiegelbeeld van $E$ in $CG$ is. Merk eerst op dat elk van de hoeken van de regelmatige zevenhoek gelijk is aan $\frac{5}{7}\times360^{\rm o}$. Vervolgens kijken we naar de vierhoek $ABCG$. Uit symmetrie volgt dat $\angle\text{AGC} = \angle\text{BCG}$. Aangezien de som van de hoeken in een vierhoek gelijk is aan $2\times360^{\rm o}$, en doordat $\angle\text{ABC} = \angle\text{BAG} = \frac{5}{7}\times360^{\rm o}$, vinden we 

$\angle\text{HGC} = \angle\text{AGC} = \frac{1}{2}\left(2 \times 360^{\rm o} - 2\times \frac{5}{7}\times360^{\rm o}\right) = \frac{2}{7}\times360^{\rm o}$.

Doordat driehoek $EFG$ gelijkbenig is vinden we bovendien 

$\angle\text{EGF} = \frac{1}{2}\left(360^{\rm o} - \frac{5}{7}\times360^{\rm o}\right) = \frac{1}{7}\times360^{\rm o}$.

Verder zien we dat 

$\angle\text{EGF} + \angle\text{EGC} + \angle\text{AGC} = \angle\text{FGH} = \frac{5}{7}\times360^{\rm o}$,

zodat 

	$\angle\text{EGC}$	$=$	$\frac{5}{7}\times360^{\rm o} - \angle\text{AGC} - \angle\text{EGF} = $
		$=$	$\left( \frac{5}{7}-\frac{2}{7}- \frac{1}{7}\right)\times360^{\rm o} = \frac{2}{7}\times360^{\rm o}$.

We zien dus inderdaad dat $\angle\text{EGC} = \angle\text{HGC}$, waaruit het gevraagde volgt.

Opgave 556 ^[ooO]

Stel dat niet alle getallen rood gekleurd zijn. Dan is er een kleinste getal dat niet rood is, we noemen dit getal $k$. Merk op dat $k > 1$ en dat $k - 1$ wel rood is, aangezien $k$ anders niet de kleinste was. Door de tweede regel weten we dat $2 \times (k - 1) = 2k - 2$ ook rood is. Bovendien is $2 \times 1 = 2$ rood en is $(2k - 2) + 2 = 2k$ duidelijk even. Nu mogen we de derde regel gebruiken om te concluderen dat

$\frac{2k}{2}=k$

ook rood is. Dit gaat echter tegen onze aanname over $k$ in. Deze tegenspraak leert ons dat alle getallen wel degelijk rood gekleurd zijn.