Over 'rechtste' en kortste wegen
[ooo]
Dit artikel bespreekt een onderwerp uit de differentiaalmeetkunde, de meetkunde van kromme lijnen en gekromde oppervlakken: de geodeet. Om tastbaar te maken wat een geodeet is, snijden we er eentje uit de schil van een flespompoen!
'De kortste verbinding tussen twee punten in het platte vlak of in de ruimte is een rechte lijn,' weet iedereen. Als een vel papier met daarop een recht lijnstuk getekend zo wordt gebogen dat het lijnstuk een kromme in de ruimte wordt, dan is de kortste verbinding tussen zijn uiteinden een recht lijnstuk dat (grotendeels) buiten het papier ligt. Maar op het vel zelf – voor een mier die over het papier loopt – is de getekende lijn nog steeds de kortste weg tussen zijn begin- en eindpunt. Dat is niet veranderd door het papier te buigen. Hoewel de rechte lijn een kromme in de ruimte is geworden, loopt de mier naar eigen idee nog steeds rechtuit zonder af te buigen naar links of naar rechts. Het is – om een andere beeldspraak te gebruiken – de weg afgelegd op een fiets waarvan het stuur vastzit. De rechte lijn is in zekere zin recht gebleven. Een lijn die binnen de beperking van een gekromd oppervlak rechtuit loopt in de betekenis zoals hier aangeduid, heet een geodeet.
Geodeten op de Cilinder
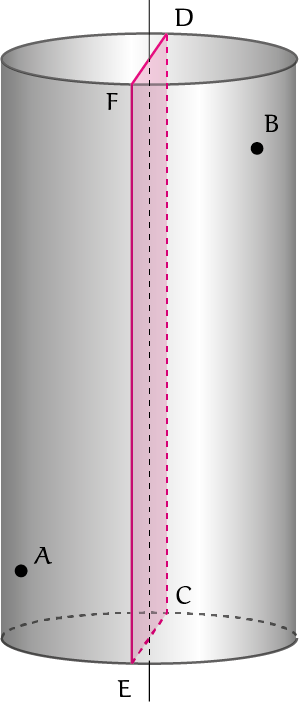
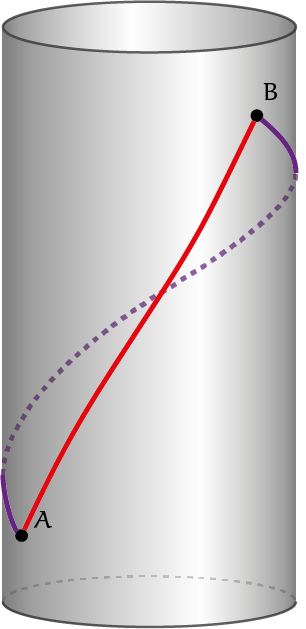
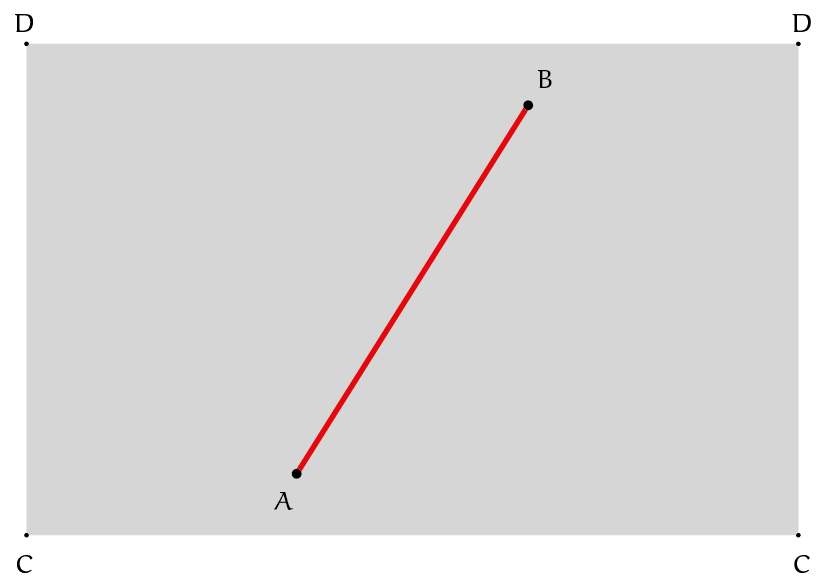
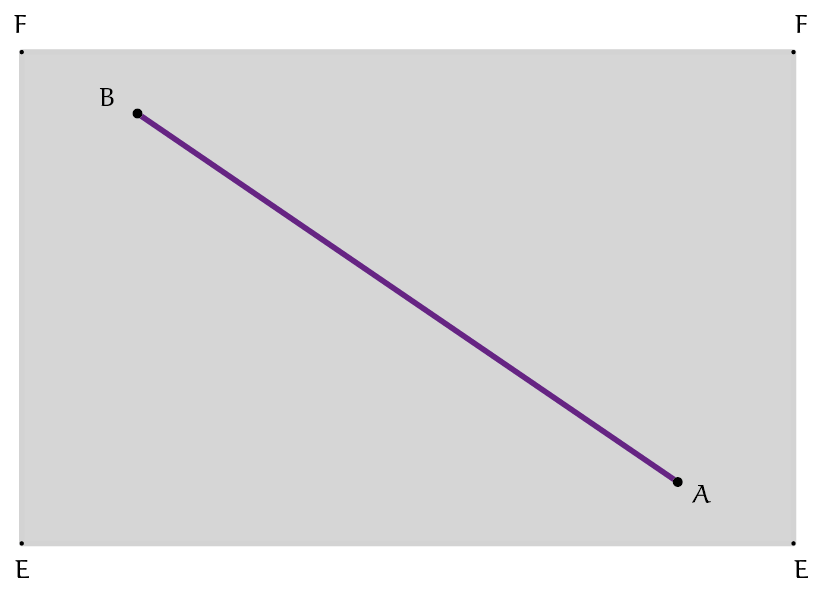
Het oppervlak van een cilinder kan worden gezien als een opgerolde rechthoek. Geodeten kunnen dan ook worden verkregen door rechte lijnen op papier te tekenen en vervolgens dat papier om een cilinder te wikkelen, dan wel dat papier tot een cilinder op te rollen. De kortste weg tussen twee punten $A$ en $B$ op een cilinder zoals in figuur 1 kan als volgt worden bepaald. Knip de cilinder langs een verticale lijn open, vouw hem uit, en trek een rechte lijn tussen de punten. Hierbij is omzichtigheid geboden in de keuze van die verticale lijn. De figuur toont twee mogelijkheden, namelijk de twee snijlijnen $CD$ en $EF$ van de cilinder en het verticale vlak waarin de as van de cilinder ligt en tot waar beide punten dezelfde afstand hebben. Bij openknippen langs $CD$ blijven de punten dicht bij elkaar, ver van die lijn. In het andere geval worden ze ver uit elkaar gehaald. Het kortste, rode rechte verbindingslijntje geeft na terugwikkelen de kortst mogelijke weg op de cilinder tussen $A$ en $B$. Als de punten op dezelfde hoogte liggen, dan is een cirkelboog in een vlak loodrecht op de as natuurlijk de kortste weg. Liggen ze recht boven elkaar, dan is een verticaal lijnstuk het kortst, en niet de schroeflijn die éénmaal rond gaat.
|
1A |
1B |
|
1C |
1D |
Het verband tussen 'de kortste weg' en het begrip 'geodeet’ is dus als volgt: de kortste verbinding is altijd een stukje geodeet (dat in het geval van de cilinder horizontaal ten hoogste $\pi$ radialen aflegt), maar niet elk stukje geodeet is de kortste weg.
Opgave 1Ga na dat op een cilinder een schroeflijn met een willekeurige constante spoed (dat is de afstand tussen de windingen) een geodeet is, en ga na met welke rechte lijnen op de opengeknipte en uitgevouwen cilinder deze overeenkomt. |
Geodeten op kegels
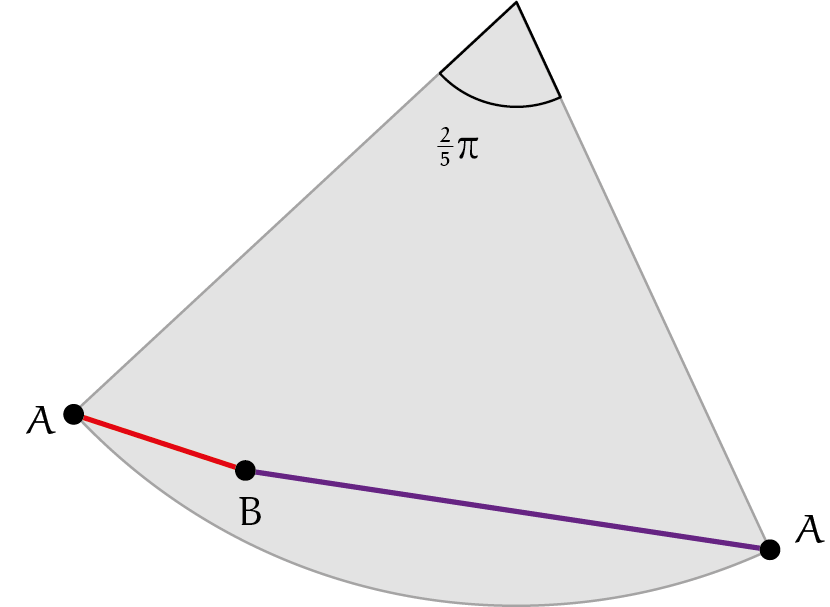
Net als de cilinder kan ook een kegel worden beschouwd als een opgerolde vlakke figuur, namelijk een cirkelsector met een bepaalde centrale hoek $\alpha$, met $0 < \alpha < 2\pi$. Geodeten en kortste wegen kunnen daarom op eenzelfde wijze worden gevonden. Een kegel wordt dan opengeknipt langs een zogenoemde beschrijvende van de kegel (een rechte lijn op het kegeloppervlak vanuit de top). Die kan (net als bij de cilinder) tussen begin- en eindpunt worden gekozen, maar ook door één van de punten (bij de cilinder had dat ook gekund). Figuur 2 toont een kegel met daarop twee punten $A$ en $B$ en de bijbehorende cirkelsector van $\alpha = \tfrac{2}{5}\pi$ radialen. Merk op dat de uiteinden van de cirkelboog beide met het punt $A$ op de kegel overeenkomen. Van de twee aangegeven geodeten op de kegel is er eentje de kortst mogelijke weg tussen $A$ en $B$.
|
2A |
2B |
|
* http://www.rdrop.com/~half/Creations/Puzzles/cone.geodesics/index.html
Geodeten algemeen
Ieder stukje van een cilinder of een kegel (behalve de top) is in feite een gebogen stukje plat vlak. Dat geldt niet voor elk oppervlak. Bijvoorbeeld een deel van een boloppervlak of een zadeloppervlak (denk aan een paardenzadel: in de ene richting hol en in de andere richting bol) kunnen niet worden platgestreken zonder vouwen en scheuren. Dan is de constructie van geodeten vanuit rechte lijnen op een vlakke figuur niet meer toepasbaar.
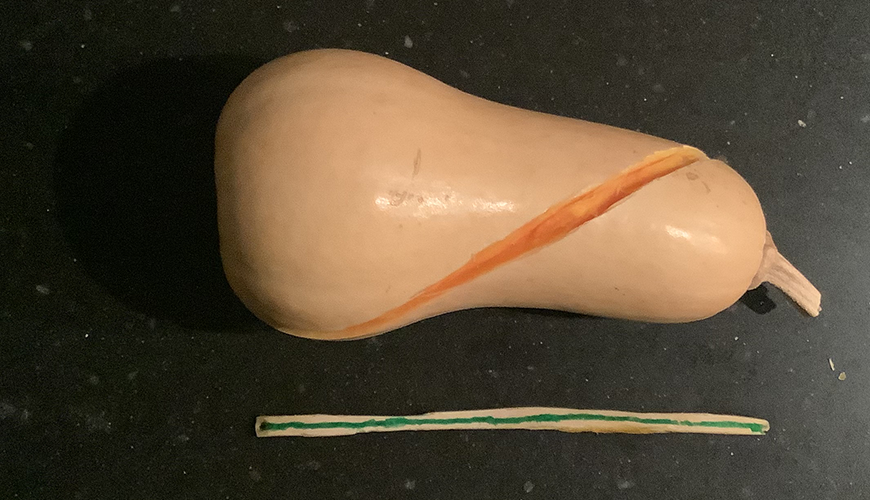
Op een bol kunnen de geodeten gemakkelijk worden aangewezen. Het artikel De stelling van Pythagoras op een bol (Pythagoras 63-2) legde uit wat over een boloppervlak de kortst mogelijke lijnen tussen punten zijn: de kortste verbinding is een stukje van de cirkel waarvan het middelpunt samenvalt met dat van de bol en waarvan de straal dus even lang is als die van de bol, een zogenoemde grootcirkel. De grootcirkels zijn de geodeten op de bol. Voor andere oppervlakken is meer theorie nodig om de geodeten te kunnen bepalen. Maar in voorkomende gevallen kan het ook experimenteel! Figuur 5 toont een geodeet op een flespompoen en maakt nog eens zijn definiërende eigenschap duidelijk. Een aangespannen draad over het oppervlak, de kortste verbinding tussen twee punten, bepaalt een lijn op de schil die nagetrokken met een viltstift, uitgesneden en plat neergelegd helemaal recht blijkt te zijn.
|
Figuur 5A |
Figuur 5B |


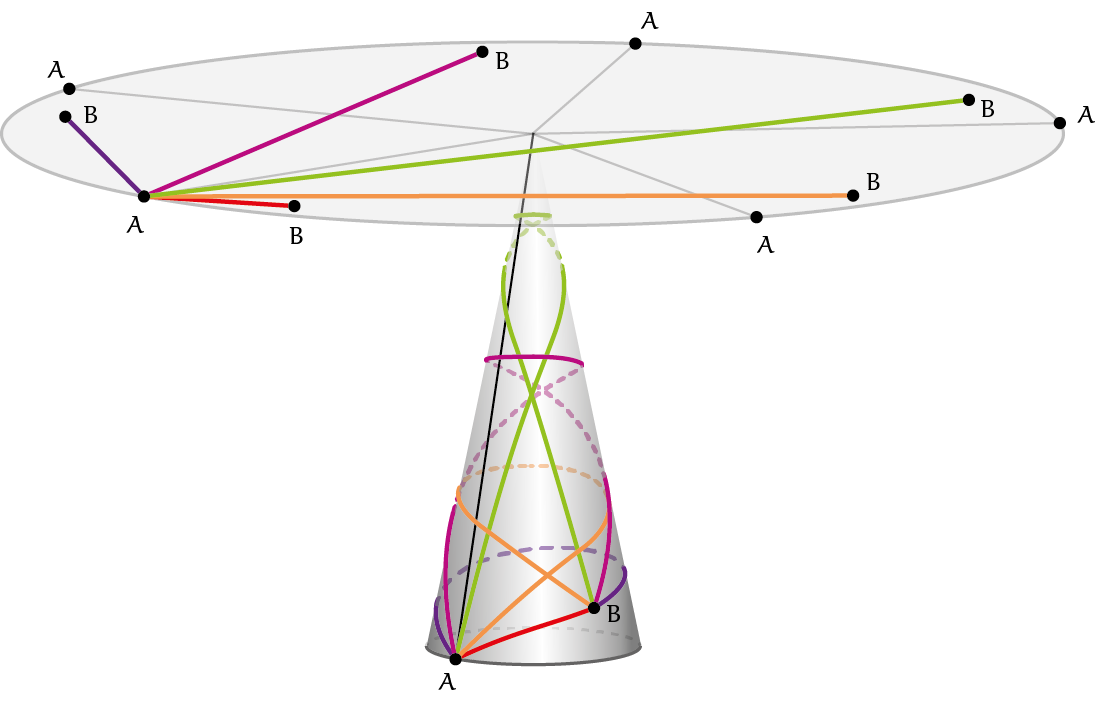 Figuur 3
Figuur 3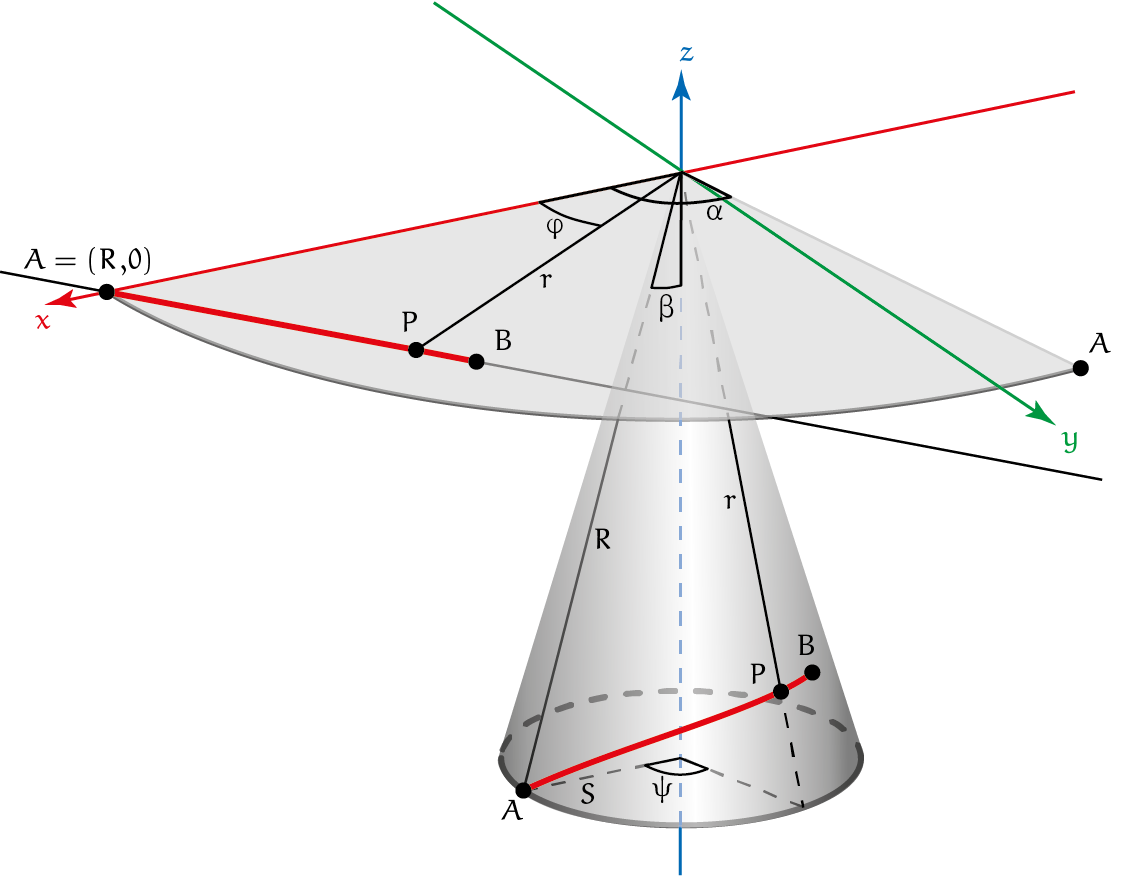 Figuur 4
Figuur 4
