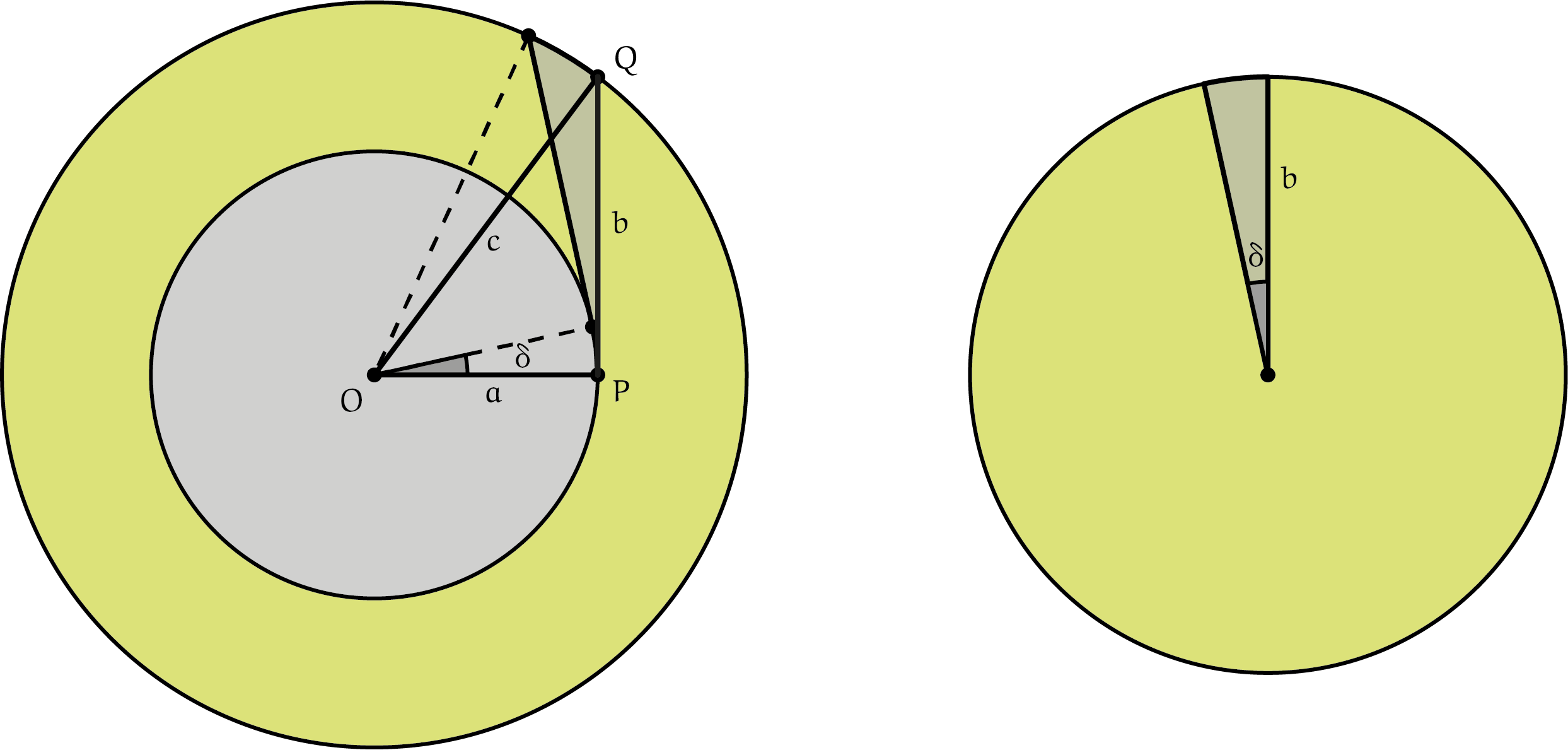
Een draaiende driehoek $OPQ$ en de ring bestreken door de zijde $PQ$. De ring en de cirkelschijf rechts hebben dezelfde oppervlakte.

Voor de stelling van Pythagoras zijn er heel veel bewijzen (zie een zestal op de achterkanten van de 60ste jaargang van dit tijdschrift en de posters). Hier geven we de volgende afleiding. Figuur 1 toont een rechthoekige driehoek $OPQ$ met rechthoekszijde $OP$ met lengte $a$, rechthoekszijde $PQ$ met lengte $b$ en schuine zijde $OQ$ met lengte $c$. Draait deze eenmaal rond het punt $O$, dan bestrijkt de zijde $OP$ een cirkelschijf met oppervlakte $\pi a^2$ en de zijde $OQ$ een cirkelschijf met oppervlakte $\pi c^2$. Het oppervlakteverschil tussen deze twee cirkelschijven, ofwel de oppervlakte van de ring ertussen, blijkt $\pi b^2$ te zijn. Daaruit volgt $a^2 + b^2 = c^2$, de stelling van Pythagoras voor de rechthoekige driehoek $OPQ$.

Dat de ring dezelfde oppervlakte heeft als een cirkelschijf met straal $b$ is als volgt in te zien. Bij een draaiing van de driehoek over een kleine hoek $\delta$ bestaat de beweging van de zijde $PQ$ grofweg uit een verschuiving in zijn eigen richting (omdat $PQ$ loodrecht op $OP$ staat) en een draaiing rond het uiteinde $P$ over dezelfde hoek $\delta$ (omdat $PQ$ over dezelfde hoek draait als $OP$). Een lijnstuk dat in zijn verlengde opschuift bestrijkt geen oppervlakte. Het draaiende lijnstuk $PQ$, dat lengte $b$ heeft, bestrijkt een cirkelsector met straal $b$ en middelpuntshoek $\delta$. Draait de driehoek in stapjes rond, dan vormen de overeenkomende cirkelsectoren een volledige cirkelschijf. (Als deze redenering je nog niet helemaal overtuigt, lees dan ook eens het artikel De tractrix in Pythagoras 56-5.)

Laat ons nu eens kijken wat er gebeurt op een bol als we dezelfde redenering proberen te volgen als hierboven.

Driehoeken op een bol

Allereerst is het zaak te begrijpen hoe drie verschillende punten op een bol een driehoek bepalen. Dat is door over het boloppervlak de kortst mogelijke lijnen tussen de drie punten te trekken. De kortste verbinding is een stukje van de cirkel waarvan het middelpunt samenvalt met dat van de bol en waarvan de straal dus even lang is als die van de bol, een zogenoemde grootcirkel. Dus een boldriehoek is een deel van een boloppervlak ingesloten door drie bogen van grootcirkels.

De lengte van een zijde van een boldriehoek, de boog van een grootcirkel tussen twee hoekpunten, is gelijk aan de straal maal de hoek in radialen tussen de twee stralen die de zijde opspannen. Elke andere verbindingskromme is langer.

Opgave 1 Teken op een bol, bijvoorbeeld een sinaasappel, een grootcirkel en overtuig jezelf ervan dat er tussen twee verschillende punten op deze cirkel geen kortere kromme bestaat.

Figuur 2 toont op een bol met straal $r$ een driehoek met middelpuntshoeken $\alpha$, $\beta$ en $\gamma$, en zijden met booglengten $a = \alpha r$, $b = \beta r$ en $c = \gamma r$. Verwar de middelpuntshoeken niet met de eigenlijke hoeken van de boldriehoek, dat zijn de hoeken tussen de raaklijnen in elk hoekpunt aan de twee grootcirkels waarop de zijden liggen. 

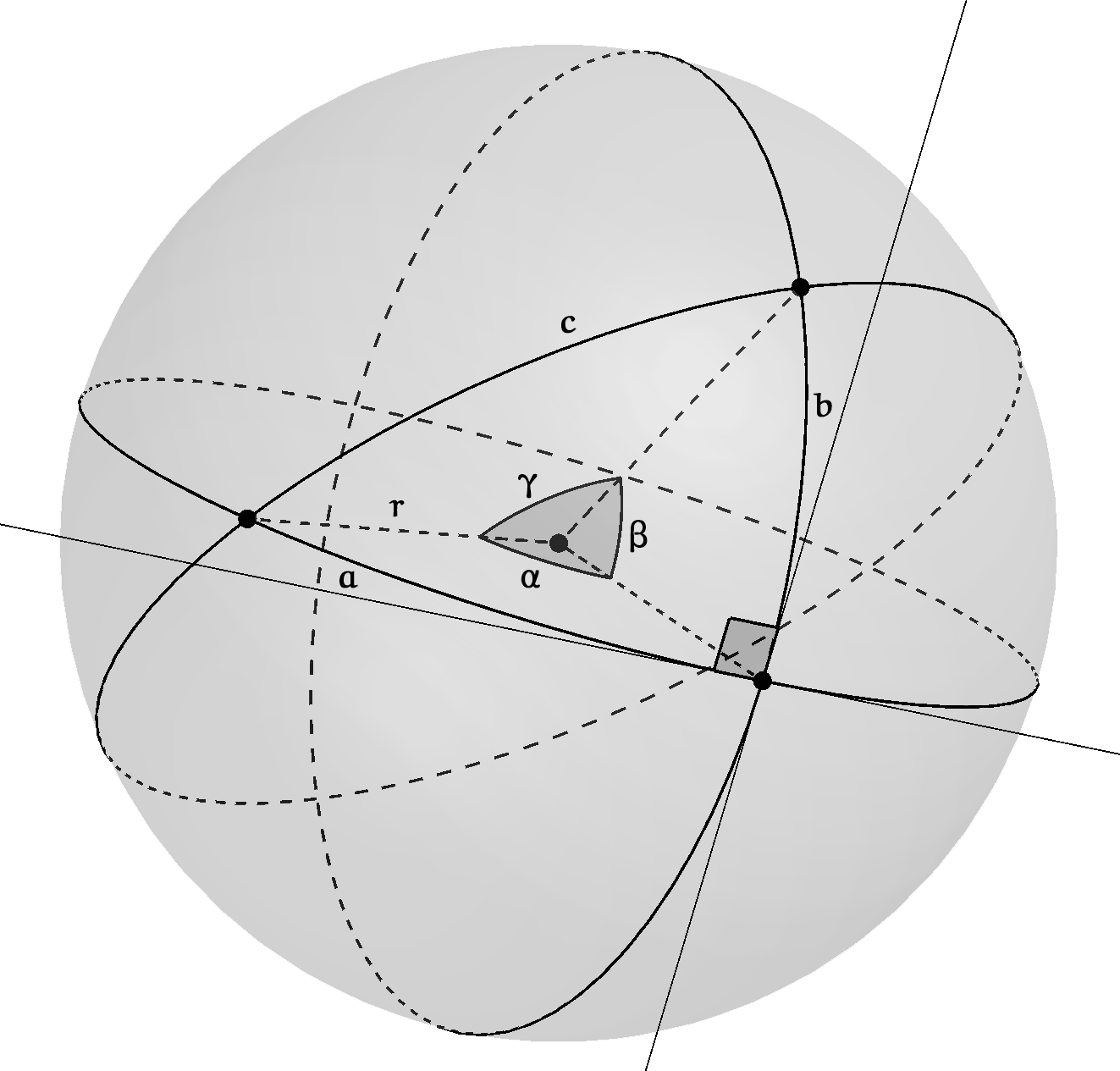
Een rechthoekige boldriehoek

De cosinusregel en de sinusregel voor de betrekkingen tussen de groottes van de hoeken en de zijden van een willekeurige vlakke driehoek hebben hun tegenhangers in de bolmeetkunde. Zover gaat dit artikel niet, maar ze zijn gemakkelijk elders te vinden (zie bijvoorbeeld het hoofdstuk 'Platte en bolle meetkunde' in het boek Speeltuin van de wiskunde). Hier gaat het alleen over driehoeken met een rechte hoek, waarvoor de stelling van Pythagoras geldt. De boldriehoek in figuur 2 is zo gekozen dat één van de hoeken een rechte hoek is.

Opgave 2 Teken op een bol driehoeken met geen, twee, en drie rechte hoeken.

Pythagoras op een bol

Een draaiende boldriehoek $OPQ$ en het bolsegment bestreken door de zijde $PQ$.

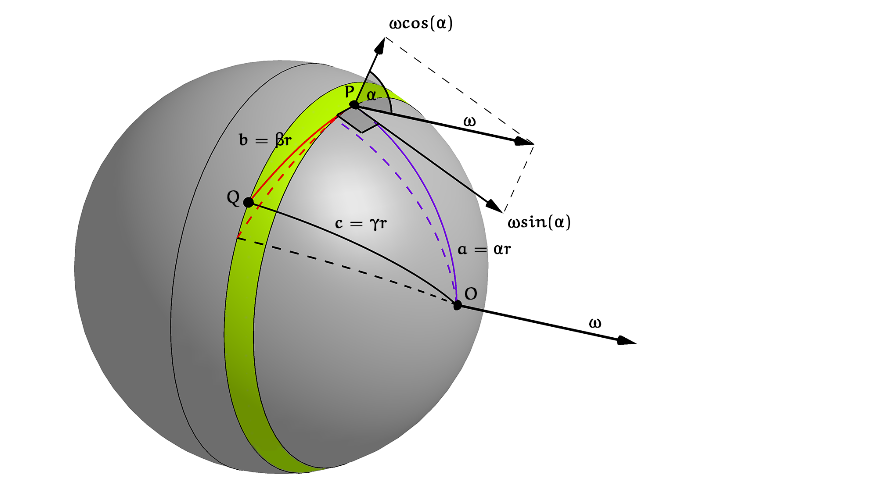
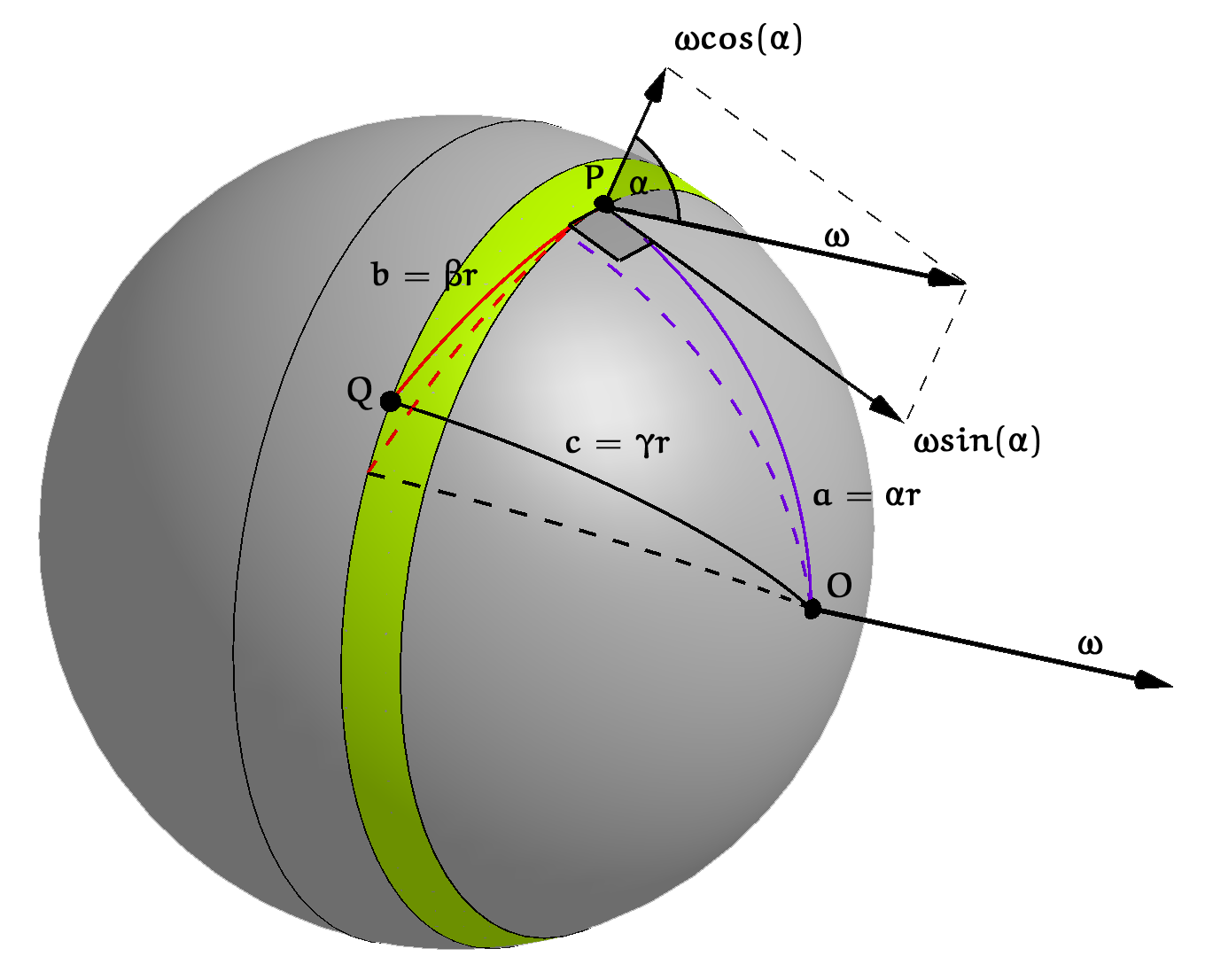
Figuur 3 toont een boldriehoek $OPQ$ met een rechte hoek in $P$. Wanneer deze driehoek om het hoekpunt $O$ draait beschrijven de andere twee hoekpunten $P$ en $Q$ elk een cirkel. De redenering verloopt vervolgens net als in het platte vlak, met in de uitwerking twee verschillen.

Het eerste verschil is onmiddellijk duidelijk: de zijden $OP$ en $OQ$ bestrijken geen cirkelschijven maar bolkappen. We moeten dus de oppervlakte van een bolkap weten.

Het tweede verschil is iets lastiger in te zien en betreft de draaiing van de zijde $PQ$: de hoek waarover deze zijde om zijn uiteinde $P$ draait (de hoek tussen de $\color{red}{rode}$ bogen) is kleiner dan de hoek waarover de andere twee zijden om $O$ draaien (de hoek tussen de $\color{purple}{paarse}$ bogen). Meer daarover verderop in dit artikel.

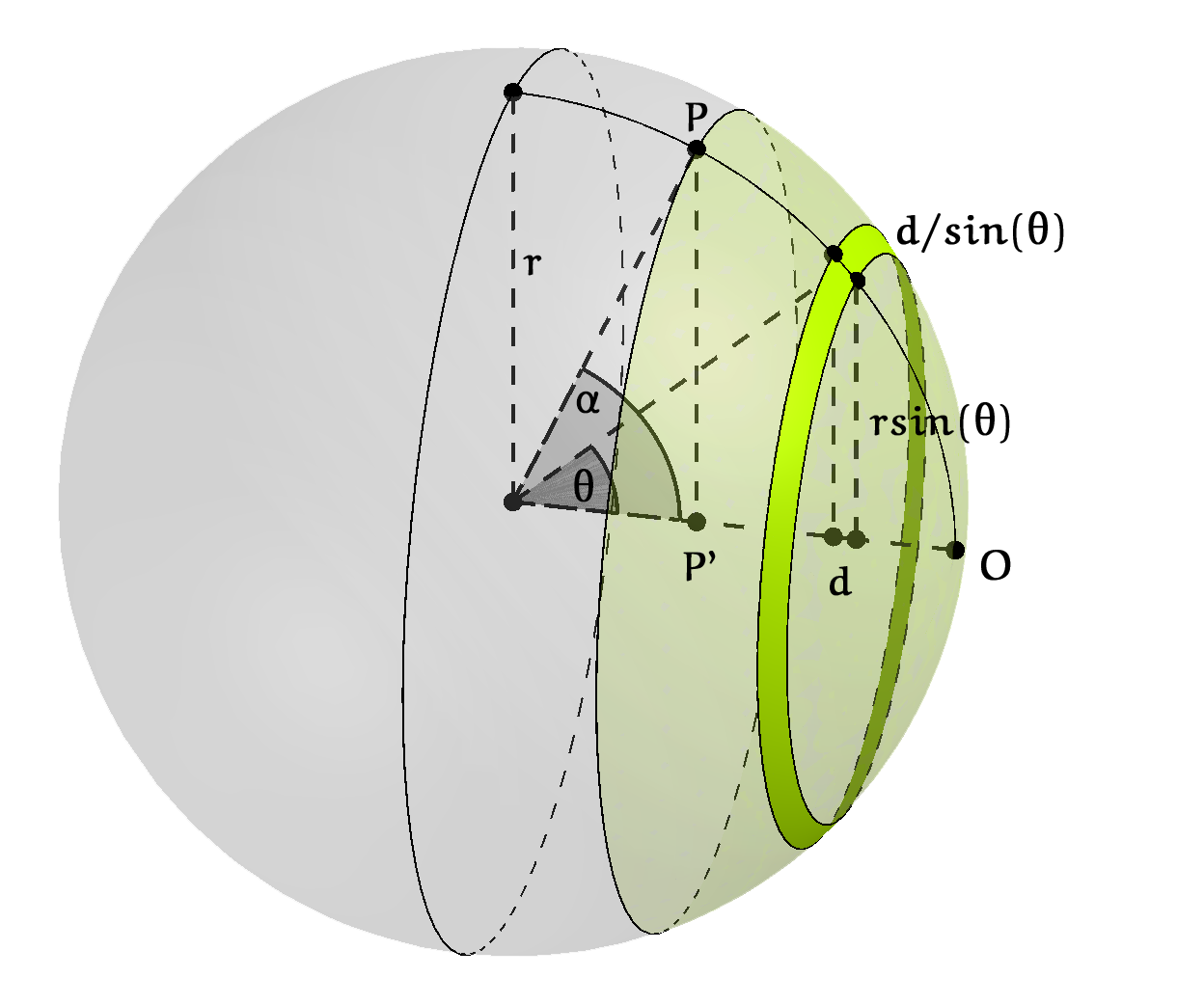
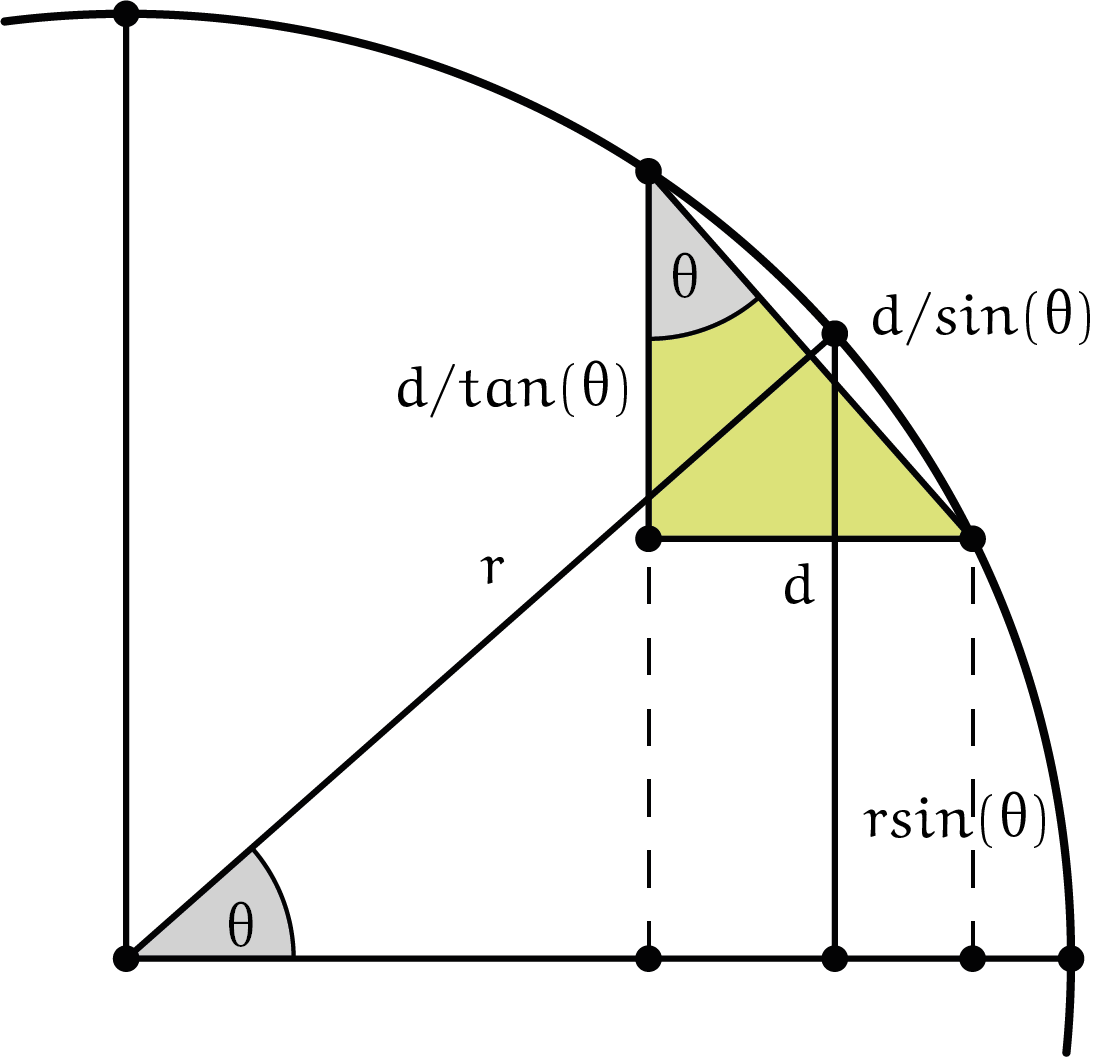
Een bolkap en een uitvergroot deel van de doorsnede.

Figuur 4 toont een bol met straal $r$ met een bolkap bepaald door een middelpuntshoek $\alpha$. Uitgelicht is een dunne schijf (segment) van de bolkap met dikte $d$ rond een middelpuntshoek $\theta, 0 < \theta < \alpha$. De breedte van de schuine rand van de dunne schijf is bij benadering $d/\sin(\theta)$. De straal van de rand ligt rond $r\sin(\theta)$, dus zijn omtrek is ongeveer $2\pi r\sin(\theta)$. De oppervlakte van de rand is dus $2\pi r\sin(\theta)\cdot d/\sin(\theta)=2\pi rd$. Merk op dat deze waarde onafhankelijk is van $\theta$ en dus geldt voor elke dunne schijf. De oppervlakte van de bolkap, opgebouwd gedacht uit dunne schijven, is daarom $2\pi r$ maal de hoogte ervan. De hoogte van de bolkap, de afstand tussen $O$ en $P'$, bedraagt $r - r\cos(\alpha)$. De oppervlakte van de bolkap is dus:

$${\rm Opp_{\rm bolkap}}(r, \alpha)=2\pi r(r-r\cos(\alpha))=2\pi r^2(1-\cos(\alpha)).$$

Opgave 3 Bereken hiermee de oppervlakte van de gehele bol.

Wanneer een bol om zijn as draait met een bepaalde hoeksnelheid $\omega$, dan is het zo dat elk punt op de bol dezelfde hoeksnelheid $\omega$ heeft. De hoeksnelheid is een vector in de richting van de draaiingsas, die kan worden ontbonden in een component loodrecht op het boloppervlak ter grootte $\omega\cos(\alpha)$ en een component rakend aan het oppervlak ter grootte $\omega\sin(\alpha)$. Zie figuur 3.

Dit is te begrijpen door te kijken naar de beweging van iemand die op de aarde op een vaste plek staat. Precies op de noordof zuidpool draait men in een dag om de eigen as, die samenvalt met de aardas. Op de evenaar draait men in een dag in een cirkel om de aardas, maar niet om de eigen as. Op alle andere plekken draait men zowel in een cirkel als om de eigen as. Draait de boldriehoek $OPQ$ met rechte hoek in $P$ eenmaal over de bol rond een as door $O$ (een van de andere hoekpunten), dan bestrijken de zijden $OP$ en $OQ$ elk een bolkap.

Bij een draaiing van de driehoek over een kleine hoek $\delta$ bestaat de beweging van de zijde $PQ$ uit een verschuiving langs zichzelf en een draaiing rond een andere as door zijn uiteinde $P$ loodrecht op de bol met hoeksnelheid $\omega\cos(\alpha)$. Daardoor draait $PQ$ in dezelfde tijdsduur slechts over een hoek $\delta\cos(\alpha)$. De bolkapsectoren die $PQ$ stap voor stap bestrijkt en die samen een bolsegment vormen, vullen rond een punt tegen elkaar gelegd dan ook niet een gehele bolkap van $2\pi$ radialen, maar slechts een sector over $2\pi\cos(\alpha)$ radialen. Zie figuur 5.

Het bolsegment uit figuur 3 en de bolkapsector hebben dezelfde oppervlakte.

Deze bolkapsector heeft oppervlakte ${\rm Opp}_{\rm bolkap}(r, \beta)\cdot\cos(\alpha)=2\pi r^2(1 - \cos(\beta))\cdot\cos(\alpha)$. De oppervlakten van beide bolkappen en hun verschil (het bolsegment dan wel de bolkapsector) voldoen aan $2\pi r^2(1 - \cos(\alpha)) + 2\pi r^2(1 - \cos(\beta))\cdot\cos(\alpha)=2\pi r^2(1 - \cos(\gamma))$, te vereenvoudigen tot:

$\begin{align*}\cos(\gamma)&=\cos(\alpha)\cdot\cos(\beta){\rm ,\ ofwel}\\
\cos(c/r)&=\cos(a/r)\cdot\cos(b/r).\end{align*}$

Dit is het verband tussen de lengten van de zijden van een rechthoekige boldriehoek – de stelling van Pythagoras op een bol!

Opgave 4 Voor kleine hoeken $\phi, 0 < \phi \ll 1$, ($\phi \ll 1$ betekent "$\phi$ is veel kleiner dan $1$") geldt: $\cos(\phi) \approx 1 - \phi^2/2$. Ga hiermee na dat voor een kleine boldriehoek $(\alpha = a/r \ll 1, \beta = b/r \ll 1, \gamma = c/r \ll 1)$ de vlakke versie van de stelling van Pythagoras als benadering verschijnt.