We nemen een eenvoudig model om de verandering in de tijd van een variabele $x$ te beschrijven. Deze variabele kan bijvoorbeeld de windsterkte op een bepaalde plek voorstellen, of de waterstand van een rivier, of nog iets anders. We laten de tijd lopen in stappen van $1$ dag. Dan is $x(1)$ de variabele op dag $1,$ en meer algemeen $x(t)$ de variabele op dag $t.$

Ga het lekker zelf doen!

We maken in dit artikel gebruik van een paar korte Python computerprogramma’s, die verderop staan. Je kunt ze direct overnemen en er zelf mee experimenteren. Op de Pythagoras website staat onder www.pyth.eu/pypy allerlei informatie over Python programmeren. De programma’s voor dit artikel zijn kant en klaar gegeven, het enige wat je nog nodig hebt is een computer die ze uit kan voeren. Als je een computer hebt waar geen Python op staat en je wilt of kunt het niet zelf installeren, ga dan met je browser naar de website jupyter.org/try en klik op “Try JupyterLab”. Je wordt naar een pagina van de site mybinder.org geleid waar je Python programma’s in Jupyter notebooks kunt uitvoeren. Klik in het menu bovenaan op File>New>Notebook, en selecteer Python3 als “Kernel”. Neem het Python programma over, tik Shift-Enter en voilà, je programma wordt uitgevoerd.

Ons model is als volgt: $x(t+1) = a \cdot x(t) + r(t),$ waarbij $a$ een constante is tussen $0$ en $1.$ De waarde van $x$ morgen (dag $t+1)$ wordt dus bepaald door de waarde van $x$ vandaag (dag $t)$ en de waarde van $r$ vandaag. De variabele $r(t)$ in dit model is een zogenaamde kansvariabele met een normale verdeling. Dat wil zeggen dat er voor iedere tijdstap opnieuw een getal willekeuring uit de normale kansverdeling wordt genomen (om precies te zijn: de normale verdeling met gemiddelde nul en standaarddeviatie één). Bijvoorbeeld $r(1)=0{,}261, r(2)= -0{,}734, r(3)=1{,}619,$ enzovoorts.

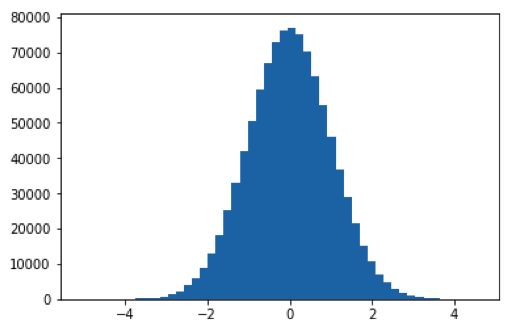
Als je heel veel getallen uit de normale verdeling neemt en er een histogram van maakt krijg je een plaatje zoals in figuur 1. Een histogram is een staafdiagram dat laat zien hoe vaak verschillende waarden voorkomen. Getallen dicht bij nul hebben de meeste kans om getrokken te worden, maar ook getallen verder weg, zeg groter dan $+2$ of kleiner dan $-2,$ komen af en toe voor. Hoe groter de absolute waarde, hoe kleiner de kans. Voor figuur 1 zijn één miljoen getallen uit de normale verdeling gebruikt. Van die één miljoen waren er zo’n $77000$ getallen tussen (ongeveer) $-0{,}1$ en $+0{,}1,$ dat geeft de hoogste staaf in het histogram in figuur 1. Als je deze figuur zelf wilt maken kun je het Python programma 1 hieronder gebruiken.

Het is overigens nog best ingewikkeld om willekeurige getallen te maken met een computer. Het voert te ver om hier te bespreken hoe je dat kunt doen, en of de getallen dan ook écht helemaal willekeurig zijn, ook al zijn het wiskundig interessante vragen (net als de vraag wat dat dan precies betekent, “echt” willekeurig). Voor nu houden we het er bij dat we in Python eenvoudig willekeurige getallen uit de normale verdeling kunnen nemen met de instructie $\mathtt{“r[i] = random.gauss(0,1)”}$, zoals in programma 1 (de normale verdeling wordt in het Engels vaak de Gaussiaanse verdeling genoemd).

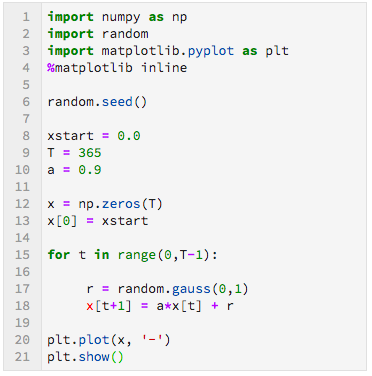
We gaan terug naar het model, $x(t+1) = a \cdot x(t) + r(t).$ We kiezen $a = 0{,}9.$ We weten hoe we de kansvariabelen $r(t)$ kunnen genereren, en daarmee zijn we klaar om ons model op een computer te simuleren. In programma 2 staat Python code waarmee het model over $T$ tijdstappen wordt gesimuleerd. Zoals je kunt zien hebben we $T$ op $365$ gezet: $365$ dagen oftewel $1$ jaar. We beginnen bij nul, dus $x(0) = 0,$ en we laten $t$ oplopen van $0$ naar $T-1.$ Iedere volgende waarde van $x$ wordt berekend door eerst een kansvariabele $r(t)$ te nemen uit de normale verdeling, en vervolgens $x(t+1) = a \cdot x(t) + r(t)$ uit te rekenen. De reeks opeenvolgende waarden van $x,$ dat wil zeggen $\{x(0), x(1), x(2), \dots, x(365)\}$ noemen we een tijdreeks. Een voorbeeld van een tijdreeks die hoort bij ons model is te zien in figuur 2, waarin de tijd $t$ op de horizontale as staat en de waarde van $x(t)$ op de verticale as. De figuur wordt gemaakt met de laatste regels van programma 2.

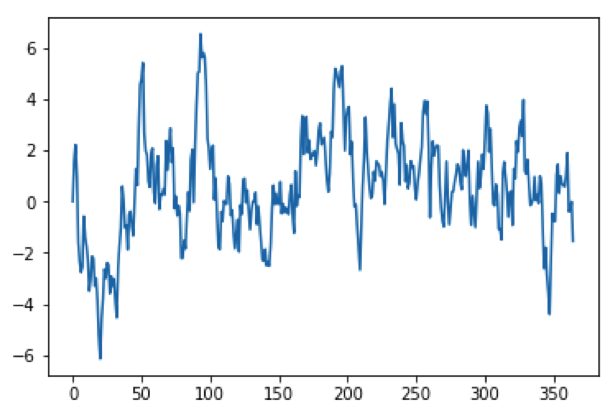
Merk op dat voor iedere nieuwe simulatie (dus iedere keer als programma 2 opnieuw uitgevoerd wordt) een nieuwe reeks kansvariabelen $\{r(0), r(1), \dots, r(364)\}$ wordt gegenereerd. Daardoor wordt het tijdsverloop van $x$ ook steeds anders.

Zelf doen

Voer programma 2 een paar keer uit. Hoe ziet de tijdreeks voor $x$ er uit bij die verschillende herhalingen? En experimenteer eens met de waarde van $a.$ In programma 2 is $a = 0{,}9$ gekozen, maar wat gebeurt er als je een ander getal kiest? Bijvoorbeeld dicht bij nul, of juist dicht bij $1$ (zeg $0{,}99)?$

In figuur 2 zien we dat bij de hoogste uitschieter, rond $t = 100, x$ even boven $6{,}0$ komt. Omdat het tijdsverloop van $x$ afhangt van de kansvariabele $r(t)$ is het een kwestie van toeval of zo’n uitschieter voor zal komen in een afzonderlijke tijdreeks voor $x.$ Laten we een drempelwaarde $h$ kiezen, bijvoorbeeld $h = 6{,}0.$ We kunnen nu de volgende vraag stellen: wat is de kans dat $x$ boven de waarde $h$ uitkomt? Om het iets preciezer te formuleren: gegeven de startwaarde $x(0) = 0$ en de eindtijd $T = 365,$ wat is de kans dat $x(t),$ met $0 \le t \le T,$ minstens één keer boven $h$ uitkomt?

Dergelijke vragen zijn belangrijk voor verschillende toepassingen. Stel dat $x$ een maat is voor de waterstand op een plek langs de kust of langs een rivier. Een uitzonderlijk hoge waterstand kan voor problemen zorgen, zoals een overstroming. Als een dijk een maximale waterstand $h$ aankan, dan is het uiteraard van belang als je iets kunt zeggen over de kans dat het water zo hoog komt.

Zelf doen

Kijk wat de hoogste waarde is die $x$ bereikt in een simulatie. Om dat makkelijk te zien kun je de regel “$\mathtt{print('maximum = ',max(x))}$” helemaal aan het einde van programma 2 toevoegen. Voer het programma een paar keer uit. Bij hoeveel simulaties komt $x$ minstens één keer boven $6{,}0?$

Ons eenvoudige model $x(t+1) = a \cdot x(t) + r(t)$ is natuurlijk geen realistisch model voor waterstand of windsterkte. Een echt realistisch model is veel gecompliceerder, met (veel) meer dan één enkele variabele. Maar dat maakt voor het voorbeeld niet uit. Onze modelvariabele $x(t)$ verandert in de loop van tijd, op een manier die grillig is maar niet volkomen willekeurig, vergelijkbaar met wat er gebeurt in realistische modellen. Daarmee is het een geschikt voorbeeld om te laten zien wat voor wiskundige vragen je kunt stellen aan zo’n model en hoe je die kunt beantwoorden.

We gaan terug naar de vraag: wat is de kans dat $x(t) > h$ zich voordoet op of voor de eindtijd $T ($dus $t \le T)$ als we beginnen op tijdstip $t=0$ met $x(0) = 0$ en $x(t)$ verder beschreven wordt door ons model? We kunnen die vraag bij benadering beantwoorden met behulp van de zogeheten Monte Carlo methode. Bij benadering wil hier zeggen: we kunnen een schatting geven van de gezochte kans, met hulp van computersimulaties van het model. Voor uiterst simpele modellen kunnen dit soort kansen soms met pen en papier exact uitgerekend worden. Maar meestal kan dat niet en moeten we de hulp van simulaties inroepen en ons tevreden stellen met een benadering of schatting van het antwoord.

Heel kort samengevat komt de Monte Carlo methode hier op neer: herhaal de simulatie een aantal keren, met iedere keer een nieuwe reeks van kansvariabelen $r(0), r(1), \dots, r(T-1).$ Noteer van iedere simulatie of daarin $x(t) > h$ voorkomt. Als we $M$ verschillende simulaties hebben gedaan, en in $Q$ van die simulaties komt $x(t) > h$ voor, dan is de schatting van de gezochte kans gelijk aan $Q/M.$

De Monte Carlo methode is in 1946/1947 bedacht door Stan Ulam en John von Neumann en is ongelooflijk veelzijdig. Ze wordt voor heel veel verschillende onderwerpen gebruikt en nog steeds verder ontwikkeld. Wiskundig valt er veel over te zeggen. We beperken ons hier tot het volgende: de schatting $Q/M$ wordt steeds beter naarmate we $M$ groter kiezen. Dus hoe vaker we de simulaties herhalen, hoe beter en betrouwbaarder het antwoord. We weten ook hoe snel het antwoord verbetert: de verwachte fout in de schatting is omgekeerd evenredig met de wortel van $M.$ Dat wil zeggen dat als we $25$ keer meer simulaties doen $(M 25$ keer zo groot), de verwachte fout een factor $5$ kleiner wordt.

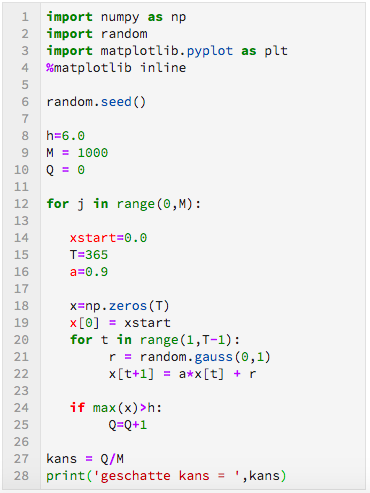
In programma 3 wordt de Monte Carlo methode gebruikt om de kans op $x(t) > h$ te schatten. De drempelwaarde $h$ is op $6{,}0$ gezet maar kan natuurlijk naar wens veranderd worden (merk op dat dan ook de kans zal veranderen!). Voor het aantal simulaties kiezen we $M = 1000.$ Als je het programma op de computer uitvoert rolt er een geschatte kans uit van ongeveer $0{,}45.$ Omdat de schatting afhangt van de gebruikte kansvariabelen $\{r(0, r(1), \dots \}$ krijg je iedere keer als je het programma opnieuw uitvoert, met steeds weer andere waarden voor $\{r(0), r(1), \dots\},$ een net iets andere schatting. Als $M$ groot is liggen die schattingen dicht bij elkaar (de te verwachten fout is klein), als $M$ niet zo groot is liggen ze verder uit elkaar (grotere fout).

Zelf doen

Kies een paar verschillende waarden voor $M,$ bijvoorbeeld $100, 1000, 10000.$ Schat de kans met programma 3 meerdere keren voor iedere waarde van $M.$ Hoe dicht liggen de antwoorden (schattingen) bij elkaar? Kun je zien dat de spreiding van de antwoorden omgekeerd evenredig is met de wortel van $M?$

Als we de drempelwaarde $h$ verhogen wordt de kans kleiner. Als de kans op een hoge waterstand of een zware storm klein is, dan is de kans op een nóg hogere waterstand of een nóg zwaardere storm natuurlijk nog wat kleiner. Met behulp van programma 3 kun je zelf makkelijk uitvinden dat bij $h = 8{,}0$ de kans ongeveer $0{,}04$ is en bij $h = 10{,}0$ tussen $0{,}001$ en $0{,}002.$ In figuur 3 zie je een voorbeeld van simulatie waarin $x(t)$ (heel even) boven $h = 10{,}0$ uitkomt.

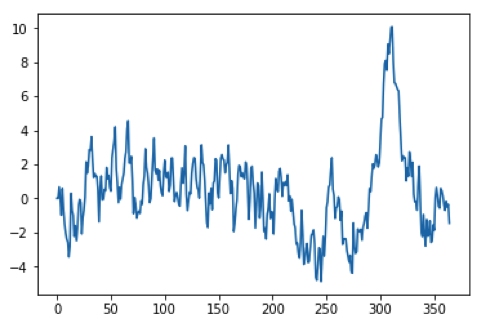
In het laatste geval, $h = 10{,}0,$ is de kans zo klein geworden dat een Monte Carlo schatting met $M = 1000$ erg onnauwkeurig is. Van de $1000$ simulaties zullen er gemiddeld nog maar één of twee de waarde $h = 10{,}0$ bereiken. Dan is het natuurlijk ook goed mogelijk dat er bij een schatting met $M = 1000$ vier simulaties $h = 10{,}0$ halen, of nul. In het eerste geval is de geschatte kans $0{,}004$ oftewel twee tot vier keer te groot, in het laatste geval is de schatting precies nul. Kortom, de relatieve fout (de fout in de geschatte kans, gedeeld door de correcte kans) is groot. Om dat te verbeteren moet $M$ groter gekozen worden. Een vuistregel voor een redelijk nauwkeurige schatting is om voor $M$ ongeveer $400$ gedeeld door de gezochte kans te kiezen. Dus bij een kans van $0{,}001$ zou je dan $M = 400000$ moeten kiezen. De gezochte kans weten we natuurlijk niet van tevoren, maar als we een eerste grove schatting hebben, zoals hierboven met $M = 1000,$ dan kunnen we $M$ aanpassen en een tweede, veel nauwkeuriger schatting maken.

Je kunt zien dat voor erg kleine kansen $M$ erg groot gekozen moet worden om een goede schatting te krijgen. Er zijn dan dus heel veel simulaties nodig, en dat maakt de Monte Carlo methode erg langzaam. Als je in programma 3 de waarde van $M$ steeds verder ophoogt, zul je merken dat het steeds langer duurt voor je een antwoord krijgt. Voor het schatten van hele kleine kansen is Monte Carlo in deze basale vorm daarom minder geschikt, en zijn alternatieve methoden ontwikkeld. Die methoden zijn sneller, maar ook gecompliceerder en minder breed inzetbaar. Wat betreft veelzijdigheid en robuustheid valt de Monte Carlo methode moeilijk te overtreffen.

Mathematics for Planet Earth!

Wist je dat wiskunde een belangrijke rol speelt in het voorspellen van weer en klimaat? Elk jaar organiseert Professor Daan Crommelin samen met anderen bijeenkomsten over wiskunde en klimaat: Mathematics for Planet Earth. In dit artikel heeft Daan Crommelin iets uitgelegd over hoe de kans op een overstroming wordt voorspeld. Programmeer en voorspel lekker mee!

In de podcastserie “De fascinatievolger” op de website van Meromorf Press, zijn er twee afleveringen speciaal aan Mathematics for Planet Earth gewijd. Je kan ze gratis beluisteren en nog veel meer interessante interviews met Wiskundigen horen. www.meromorfpress.co.uk

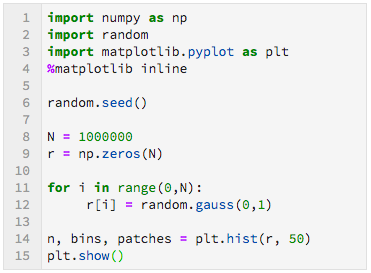
Python code voor histogram van de normale verdeling. Het array $\mathtt{r}$ wordt gevuld met $N$ verschillende willekeurige getallen uit de standaard normale verdeling die gemiddelde $0$ en standaard deviatie $1$ heeft.

Python code om model $x(t+1) = a \cdot x(t) + r(t)$ te simuleren. Starttijd is $t=0,$ eindtijd is $t+1 = T$ oftewel $t =T-1.$

Python code om de kans op $x(t) > h$ te schatten met behulp van de Monte Carlo methode.