Het was een spectaculair gezicht: rokende hoogspanningsleidingen die over een aantal kilometers vlák boven de weilanden in Flevoland hingen. Op de achtergrond grote steekvlammen. Hoewel dit een heel gevaarlijke situatie was, zijn er op die hectische momenten toch geen persoonlijke ongelukken gebeurd. Ook op het spoor, waar de bovenleiding werd geraakt door de gezakte hoogspanningsleidingen, wist de machinist de trein op tijd te stoppen.

In dit artikel gaan we de lengte van de hoogspanningsleidingen berekenen. Dat doen we door eerst een aantal benaderingen te gebruiken: een rechte lijn, een cirkel en een parabool. De werkelijke vorm van de leiding is een kettinglijn. Die berekenen we ook. Wat we als eerste willen weten is hoeveel langer de leidingen zijn geworden, maar het is misschien ook leuk om te weten hoe goed de benaderingen zijn.

HoOgspaNningsleIdiNGen

Door heel Nederland lopen hoogspanningsleidingen om stroom te vervoeren. Op veel plaatsen hangen die bovengronds aan hoogspanningsmasten. Uiteraard zó hoog dat ze normaal gesproken geen gevaar opleveren. De meeste hoogspanningsmasten in Nederland zijn tussen de $54$ en $60$ meter hoog en ze staan $350$ tot $400$ meter uit elkaar. De lijnen hangen in een boog, in het midden tussen twee masten hangt de lijn dan het laagst, op zo'n $40$ meter.

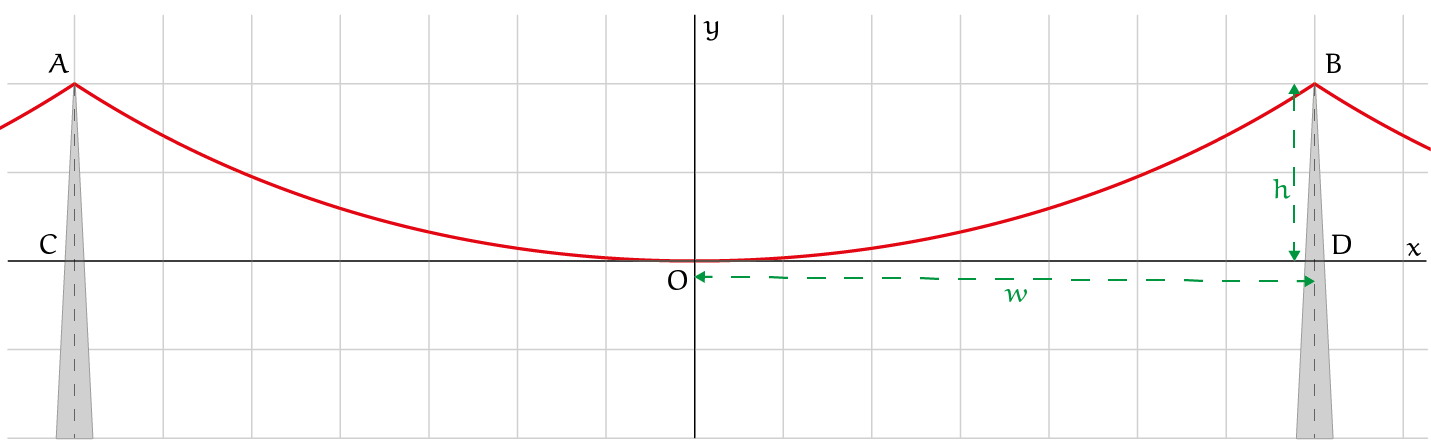
In figuur 1 staat dit versimpeld afgebeeld. Voor de berekeningen straks is het handig om een assenstelsel te nemen waar het laagste punt van de leiding samenvalt met de oorsprong. In de figuur zijn de belangrijkste maten benoemd: de afstand van de mast tot het laagste punt (dus de helft van de afstand tussen twee masten, in de figuur lengte $OD$) noemen we $w$ en de het hoogteverschil tussen het laagste en het hoogste punt van de leiding (in de figuur lengte $BD$) noemen we $h$. In Flevoland is het voornamelijk een landelijk gebied, daar hangen de leidingen niet zo hoog. Het ophangpunt zit op ongeveer $26\,m$ en het laagste punt op ongeveer $15\,m$. Daaruit volgt $h = 26 - 15 = 11\,m$. De afstand tussen de masten is daar $350\,m$. Daarmee is $w = 350/2 = 175\,m$.

Vanwege de symmetrie hoeven we in het vervolg alleen de rechterhelft van figuur 1 te gebruiken.

ReChte lijn

Als de leiding precies horizontaal zou lopen, zou deze even lang zijn als de afstand tussen twee masten. Ze hangen echter met die boog, wat betekent dat de leiding langer moet zijn. Hoeveel langer? Dat kunnen we uitrekenen als we weten wat voor formule de leiding tussen te twee punten beschrijft.

Het allersimpelst is het om aan te nemen dat de leiding in een rechte lijn naar het laagste punt gaat en daarna weer in een rechte lijn omhoog. Dan kunnen we eenvoudig met behulp van de stelling van Pythagoras de afstand berekenen.

Opgave 1 Bereken de lengte van het lijnstuk $OB$ uitgedrukt in $w$ en $h$. En hoe groot is de lengte dan met $w = 175$ en $h = 11$?

Cirkel

Iets minder simpel is het om net te doen alsof de leiding een cirkel volgt. Die cirkel moet dan gaan door de drie punten $A$, $O$ en $B$ in figuur 1. De cirkel die we zoeken is de omgeschreven cirkel van de driehoek $AOB$. Het middelpunt van die cirkel is het snijpunt van de drie middelloodlijnen van de zijden. Omdat het laagste punt in het midden zit hebben we een gelijkbenige driehoek waarvan één middelloodlijn ook nog eens samenvalt met de $y$-as. We hoeven dus alleen nog de middelloodlijn van $OB$ te bepalen. Het middelpunt $M$ van de omgeschreven cirkel is dus het snijpunt van die middelloodlijn en de $y$-as.

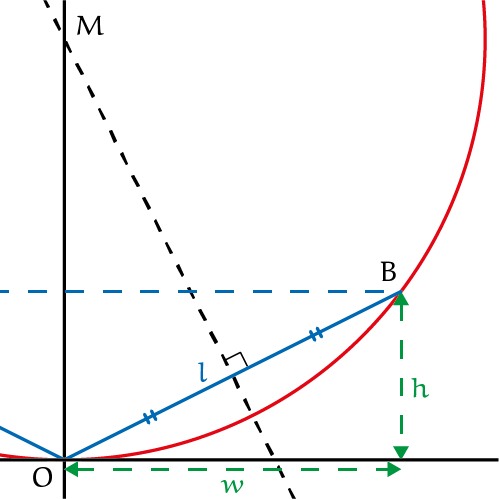
Opgave 2 Bepaal, met $w = 175$ en $h = 11$, de vergelijking van die middelloodlijn en daarmee de straal van de cirkel.

Met de straal van de cirkel weten we ook de omtrek. Om te weten welk deel van de cirkel de lengte van de boog $OB$ uitmaakt moeten we nog hoek $OMB$ bepalen. Deze hoek (in radialen) maal de straal geeft ons booglengte $OB$.

Opgave 3 Bepaal hoek $OMB$ en booglengte $OB$.

De berekeningen hierboven willen we straks nog eens doen met de langere leidingen. Daarom willen we de booglengte kunnen uitdrukken in $w$ en $h$.

De vergelijking van lijnstuk $l$ kunnen we eenvoudig bepalen: de lijn gaat door de oorsprong en de richtingscoëfficiënt is $h/w$. Dus $l : y = h/w \cdot x$. Deze lijn is de zijde van de driehoek waar we de middelloodlijn, laten we die $m$ noemen, voor moeten bepalen. De andere middelloodlijn is immers de $y$-as en we weten ook dat de drie middelloodlijnen elkaar in het punt $M$ snijden.

Het midden van lijnstuk $l$ is $(w/2, h/2)$. Verder weten we dat de richtingscoëfficiënt van de loodlijn het omgekeerde en tegengestelde is van de richtingscoëfficiënt van de lijn zelf: $m : y = -w/h \cdot x + b$. We kunnen $b$ bepalen door het middelpunt in te vullen: $-w/h \cdot w/2 + b = h/2$ dus $b = h/2 + w^2/(2h)$. Deze $b$ geeft ons ook het snijpunt met de $y$-as, wat juist het middelpunt van de cirkel is. De straal van deze cirkel is daarmee gelijk aan

$$r=\frac{h}{2}+\frac{w^2}{2h}.$$

Het stuk tussen van de cirkel tussen de mast en het laagste punt kunnen we vinden door eerst $a = \angle OMB$ te bepalen. Die hoek is gelijk aan $\tan^{-1}\left(\frac{w}{r-h}\right)$.

De lengte van boog $OB$ komt dan uit op

$$r\cdot\tan^{-1}\left(\frac{w}{r-h}\right).$$

Parabool

Ook de cirkel is een benadering. Zoals gezegd volgt de leiding een zogeheten kettinglijn. Deze is al eerder beschreven in Pythagoras 46-4. Een kettinglijn beschrijft de vorm van een draad, of ketting, die vrij tussen twee punten hangt, zoals een lege waslijn of dus een hoogspanningsleiding. Sinds de oudheid werd gedacht dat die boog een parabool was, pas in de tijd van Christiaan Huygens werd bewezen dat het geen parabool kon zijn. Zodra je was (gelijkmatig) aan die lijn gaat hangen wordt de vorm wél een parabool. Die vorm krijg je ook als je bijvoorbeeld een hangbrug maakt: de tuidraden dragen dan het wegdek, waardoor ook weer die parabool ontstaat. Laten we eerst dan maar kijken wat de benadering met een parabool ons oplevert.

Om de formule van de parabool op te stellen kunnen we gebruik maken van de vorm $y = ax^2$, want de top van onze parabool zit in de oorsprong.

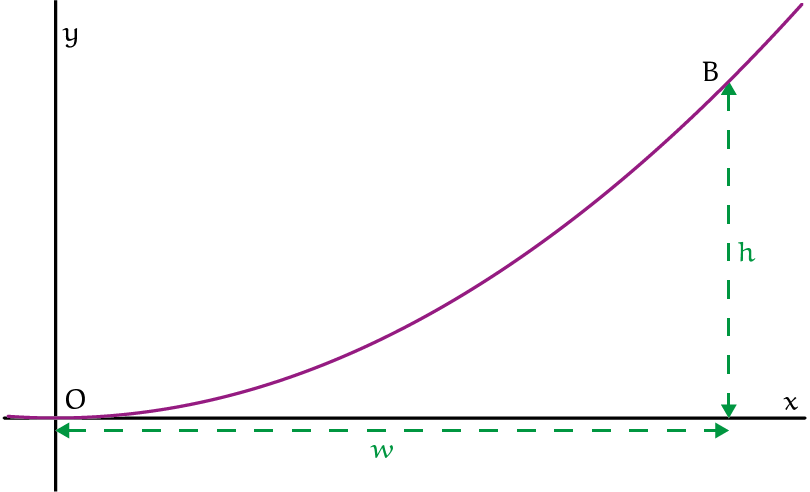
Opgave 4 Druk de waarde van $a$ in $y = ax^2$ uit in $h$ en $w$ door gebruik te maken van figuur 4.

Nu we de formule voor de parabool hebben komt het lastigste stuk, het bepalen van de lengte van de grafiek tussen de twee uiteinden. Er is een algemene formule voor de lengte $L$ van de grafiek van $f(x)$ op het interval $[u, v]$:

$$L=\int_u^v\sqrt{1+f'(x)^2}\,{\rm d}x.$$

Uit opgave 4 kwam als het goed is $a = \frac{h}{w^2}$, dus de formule van de parabool is $f(x) = \frac{h}{w^2}x^2$, wat de afgeleide $f'(x) =\frac{2h}{w^2}x$ geeft. Daarmee wordt de lengte van de grafiek van $f$ tussen $x = 0$ en $x = w$ gelijk aan

$$L=\int_0^w\sqrt{1+\frac{4h^2}{w^4}x^2}\,{\rm d}x.$$

Deze rekenen we uit met de grafische rekenmachine (of met GeoGebra of Desmos). Met de waarden voor $h = 11$ en $w = 175$ krijgen als oplossing ongeveer $175{,}4599\ m$. Dit is net iets anders dan de booglengte die je bij opgave 3 zou hebben gevonden $(175{,}4606\,m)$. Over een lengte van meer dan $175$ meter is het verschil in booglengte tussen de parabool en de cirkel dus $0{,}7\,mm$!

De kettinglijn

Tot zover de benaderingen. Om de lengte van de leiding zo precies mogelijk te berekenen zouden we de formule van de kettinglijn op moeten stellen. In het kader kun je meer lezen over de kettinglijn.

		Kettinglijn en Cosinus hyperboliCusPas na de ontwikkeling van calculus door Isaac Newton en Gottfried Leibniz kon de werkelijke formule voor de kettinglijn worden bepaald. Die is (door de oorsprong):  $$f(x)=\frac{1}{\lambda} (\cosh(\lambda x)- 1).$$ In deze formule is $\cosh(x)$ de cosinus hyperbolicus. De sinus en cosinus hyperbolicus gaan niet uit van een cirkel, zoals de 'gewone' sinus en cosinus (waar geldt: $\sin^2(x) + \cos^2(x) = 1$) maar van een hyperbool. Dan geldt $\cosh^2(x) - \sinh^2(x) = 1$. Verder hebben we nog nodig dat de afgeleide van $\cosh(x)$ gelijk is aan $\sinh(x)$ en de afgeleide van $sinh(x)$ is $\cosh(x)$. Parameter $\lambda$ bepaalt hoe steil de boog van de kettinglijn is. We willen dat onze kettinglijn door de oorsprong gaat en door het punt $B(w, h)$. Oftewel $$f(w)=\frac{1}{\lambda}(\cosh(\lambda w)-1)=h.$$ De waarde $w$ en $h$ zijn bekend, die kunnen we dus invullen. Dan houden we een vergelijking over met onbekende $\lambda$. Met onze GR kunnen we deze vergelijking oplossen. Op sommige rekenmachines kan dit direct, op andere heb je de definitie $$\cosh(x)=\tfrac{1}{2}\left({\rm e}^x+{\rm e}^{-x}\right)$$ nodig. Dan krijgt de kettinglijn de formule $$f(x)=\frac{1}{2\lambda}\left({\rm e}^{\lambda x}+{\rm e}^{-\lambda x}-2\right).$$ Met $h = 11$ en $w = 175$ vullen we in onze GR de vergelijking $(\cosh(175\star X)-1)/X=11$ in. Wel goed om te weten dat in ons geval $\lambda$ (dus $X$ in de GR) heel klein is, ergens tussen de $0$ en $0{,}002$. Als oplossing vinden we $\lambda = 0{,}0007174244\dots$.

We hebben dus de formule

$$f(x) =\frac{1}{\lambda}(\cosh(\lambda x)-1)$$

en we hebben de $\lambda$ gevonden. Voor de lengte van de hoogspanningsleiding hebben we nu weer de booglengte nodig. In die formule komt $f'(x)$ voor, in het kader hebben we kunnen lezen dat $(\cosh(x))' = \sinh(x)$. De formule voor de booglengte wordt dan

$$L=\int_0^w\sqrt{1+\sinh^2(\lambda x)}\,{\rm d}x.$$

Omdat we in het kader ook hadden gezien dat $cosh^2(x) - sinh^2(x) = 1$ krijgen we dus

$$L=\int_0^w\sqrt{\cosh^2(\lambda x)}\,{\rm d}x = \int_0^w\cosh(\lambda x)\,{\rm d}x.$$

Volgens datzelfde kader geldt $(\sinh(x))' = \cosh(x)$, dus is, omdat $\sinh(0) = 0$, de integraal eenvoudigweg

$$\sinh(\lambda w)/\lambda.$$

Invullen van $\lambda = 0{,}0007174244\dots$ en $w = 175$ geeft een booglengte van $175{,}4601\,m$. Het verschil met de parabool is $0{,}2\,mm$ en met de cirkel is het ook maar $0{,}5\,mm$. Dat zijn dus best redelijke benaderingen.

De kortsluiting

Op de bewuste 2 september 2022 trad er in Flevoland kortsluiting op en raakte de hoogspanningsleiding de bovenleiding op de spoorlijn Lelystad – Zwolle. Gegevens over hoe laag de hoogspanningsleiding precies is gekomen hebben we niet. Voor het berekenen van het nieuwe laagste punt van de hoogspanningsleiding moeten we nu iets meer weten over de bovenleiding zelf. Die hangt gemiddeld op $5{,}5\,m$ boven het spoor. Daarboven zijn ook nog ophangdraden. Verder hoeven de draden elkaar niet letterlijk te raken om een vonk over te laten springen bij dit soort spanningen. Voor het vervolg van het verhaal ga ik ervan uit dat de hoogspanningsleiding nu op het laagste punt op $7\,m$ kwam, $8$ meter lager dan normaal.

De enige verandering in de berekeningen is nu dat de waarde van $h$ nu $26 - 7 = 19\,m$ is geworden. Ter plaatse loopt de spoorlijn ook zo goed als midden onder het laagste punt. We mogen dan ook $w = 175$ laten.

Voor de rechte-lijn benadering kunnen we de nieuwe waarde van h invullen, we krijgen nu een lengte van $176{,}0281\,m$. Bij de cirkelbenadering krijgt de cirkel een kleinere straal: de 'bolling' wordt groter. Met het invullen van de nieuwe waarde voor h krijgen we een straal van de cirkel van $815{,}421\,m$. Daartegenover staat dat we een groter deel van de cirkel tussen de hoogspanningsmasten krijgen: $\angle AMO$ wordt groter, namelijk $0{,}21629\,{\rm rad}$. Daarmee wordt de lengte van de cirkelboog $815{,}421\dots \cdot 0{,}21629\dots \approx 176{,}3720\,m$.

De nieuwe formule voor de parabool wordt $y = \frac{19}{175^2}x^2$ en de lengte van de parabool tussen de top van de mast en het laagste punt vinden we weer met de grafische rekenmachine. Nu komt er ongeveer $176{,}3657$ uit. De kettinglijn krijgt ook een nieuwe parameter die we weer met de GR uitrekenen: $\lambda = 0{,}0012359\dots$, waarna we de booglengte weer kunnen uitrekenen met $\sinh(\lambda w)/\lambda$. Daar komt nu ongeveer $176{,}3678$ uit. Je ziet dat door het lager hangen van de leiding de benaderingen wat meer uiteen gaan lopen. In de tabel hieronder staan de benaderingen bij elkaar in meters:

	normaal	kortsluiting	verschil
lijn	$175{,}3454$	$176{,}0284$	$0{,}683$
cirkel	$175{,}4606$	$176{,}3720$	$0{,}911$
parabool	$175{,}4599$	$176{,}3657$	$0{,}906$
kettinglijn	$175{,}4601$	$176{,}3678$	$0{,}908$

Behalve de lijnbenadering komen ze alle drie op een verschil van (afgerond) $91\,cm$ uit. Dit moeten we nog wel vermenigvuldigen met $2$, omdat we steeds maar de helft hebben berekend. Dus om de hoogspanningsleiding $8$ meter lager te laten hangen is er afgerond $1{,}81$ à $1{,}82\,m$ extra leiding nodig op en totale lengte van meer dan $350\,m$.

Als we in één figuur op schaal de drie benaderingen en de kettinglijn willen tonen vallen de cirkel, parabool en kettinglijn niet te onderscheiden. Wel te begrijpen dus dat men in de oudheid het verschil niet kon zien. In andere gevallen moet je wel opletten met de benaderingen. Als $w$ niet $175$ maar bijvoorbeeld $38\,m$ zou zijn, dan zien de drie krommen eruit als in figuur 5. 

Dan zijn de verschillen wel wat groter.