
Poolbiljarten: diverse moeilijkheden bij het potten
Naar aanleiding van het Smartpoolscholenproject besteedt Pythagoras dit schooljaar in een serie nummers aandacht aan verschillende (wiskundige) aspecten van het poolbiljarten. In dit vierde artikel uit de serie leer je over de moeilijkheden bij het potten van de object ball in een pocket.
Om te beginnen krijg je enkele maten van pooltafels, ballen en pockets. De meeste pooltafels hebben een lengte-breedteverhouding van 2:1. De kleinste, een zogenaamde 6-foottafel (6ft), is 180 cm bij 90 cm. Dit zijn de afmetingen van het speelveld. Er zijn ook 7ft (de maat van de smartpooltafels), 8ft en 9ft-tafels. 9ft is het wedstrijdformaat en meet 254 cm bij 127 cm. De ballen die op deze tafels worden gebruikt hebben een doorsnede van 57,2 mm.
Wist je dat?
Bij veel pooltafels betaal je per wedstrijd met een muntinwerpsysteem. De object balls verdwijnen na het potten in het opbergcompartiment en komen niet meer tevoorschijn tot er opnieuw betaald is. Maar een onbedoeld gepotte cue ball moet natuurlijk weer in het spel terugkeren en wordt naar een opening aan de zijkant van de tafel geleid. Deze scheiding kan worden gerealiseerd door de cue ball iets groter te maken. Omdat het verschil in grootte van de ballen het spel aanzienlijk beïnvloedt, worden er ook tafels gemaakt met een magneetsysteem. Alle ballen zijn dan even groot, maar in de kern van de cue ball is een magneet gebouwd. Wanneer de magnetische bal een detector passeert, activeert een schakelaar de goot naar de opening.
We versimpelen de situatie in dit artikel, zodat de hoekpunten $L_P$ en $R_P$ ($L$ = links, $R$ = rechts, $P$ = pocket) van de banden met de pocket op een afstand van $4r$ van elkaar liggen ($r$ is de straal van een bal). Bovendien laten we de hoeken $L_P$ en $R_P$ recht zijn (zie de blauwe driehoekjes, toegevoegd in figuur 1).
De Foutmarge
Om een object ball $O$ te kunnen potten zal je deze nauwkeurig moeten raken. Het is belangrijk om te beseffen dat de afstand van de object ball tot de pocket de grootste rol speelt bij deze nauwkeurigheid. De lijn die een object ball volgt naar de pocket noemen we de target line.
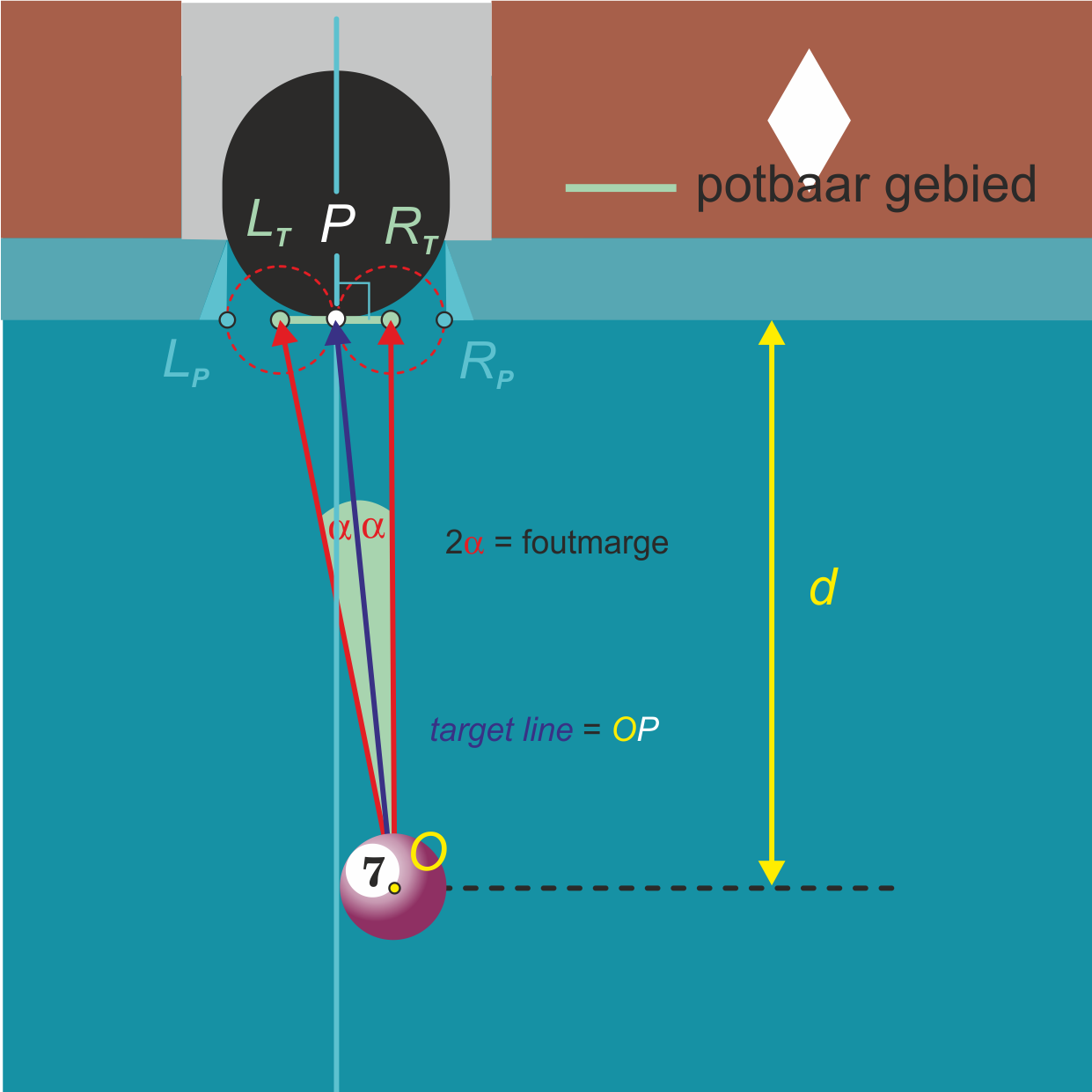
Het potbare gebied is het gebied waartussen het middelpunt van de object ball gericht moet worden om rechtstreeks in de pocket te kunnen rollen. In figuur 1 is het potbare gebied het (groene) lijnstuk $L_TR_T$ ($T$ = target), ter lengte van twee keer de straal $r$ van een bal. Het punt $L_T$ ligt op afstand $r$ van de linkerhoek van de pocket $L_P.$ Het punt $R_T$ ligt op afstand $r$ van de rechterhoek van de pocket $R_P.$
Wanneer je de uiterste target lines tekent $(OL_T$ en $OR_T)$ waarover een object ball nog gepot kan worden ontstaat $\angle L_TOR_T = 2\cdot\alpha$ die we de foutmarge noemen. De foutmarge is de marge die je je kunt veroorloven om de bal nog net te potten.
Stelling:
De foutmarge neemt af naarmate de afstand tot de pocket toeneemt.
Om dit te bewijzen bekijken we situaties waarbij de object ball recht voor de pocket ligt, op de pocket centerline (figuur 2). De pocket centerline is de middelloodlijn van het lijnstuk $L_PR_P.$ We nemen voor de breedte van de pocket $4r,$ en voor de diameter van een bal $2r.$
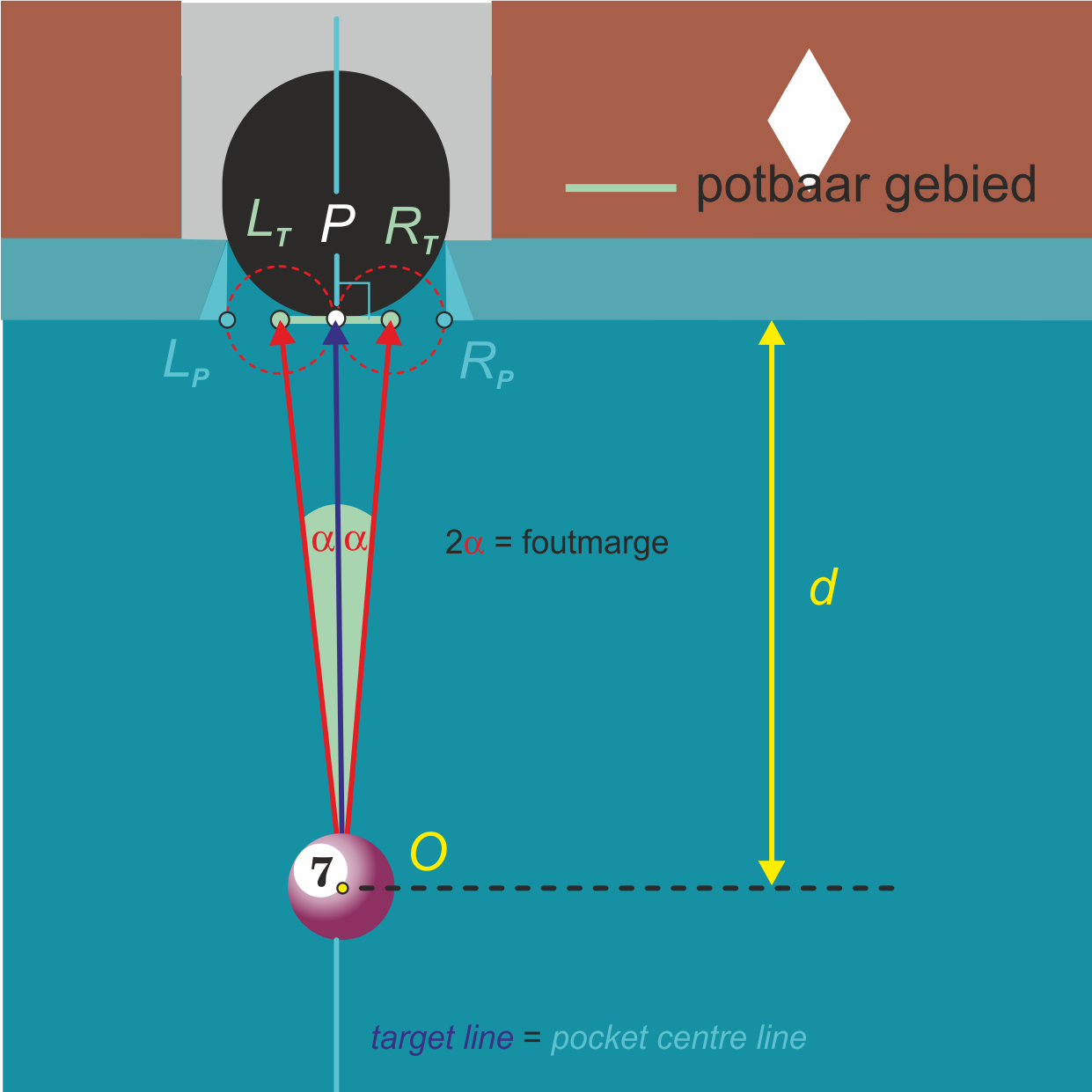
Wanneer we de object ball op de pocket centerline leggen, op afstand $d$ van de band (lijn door $L_P, L_T, P, R_T, R_P)$ geldt:
De foutmarge is $2\cdot\alpha=2\cdot\tan^{-1}\left(\frac{r}{d}\right).$
Opgave 1
Toon dat aan.
Opgave 2
Voor de volgende opdracht nemen we $r = 3$ cm.
a) Vanaf welke afstand $d$ is de foutmarge $90^{\rm o}?$
b) Bereken de foutmarge bij $d = 5, 10, 15, 20, 25$ en $30$ cm.
Het effectieve deel van de pocket (potbare gebied)
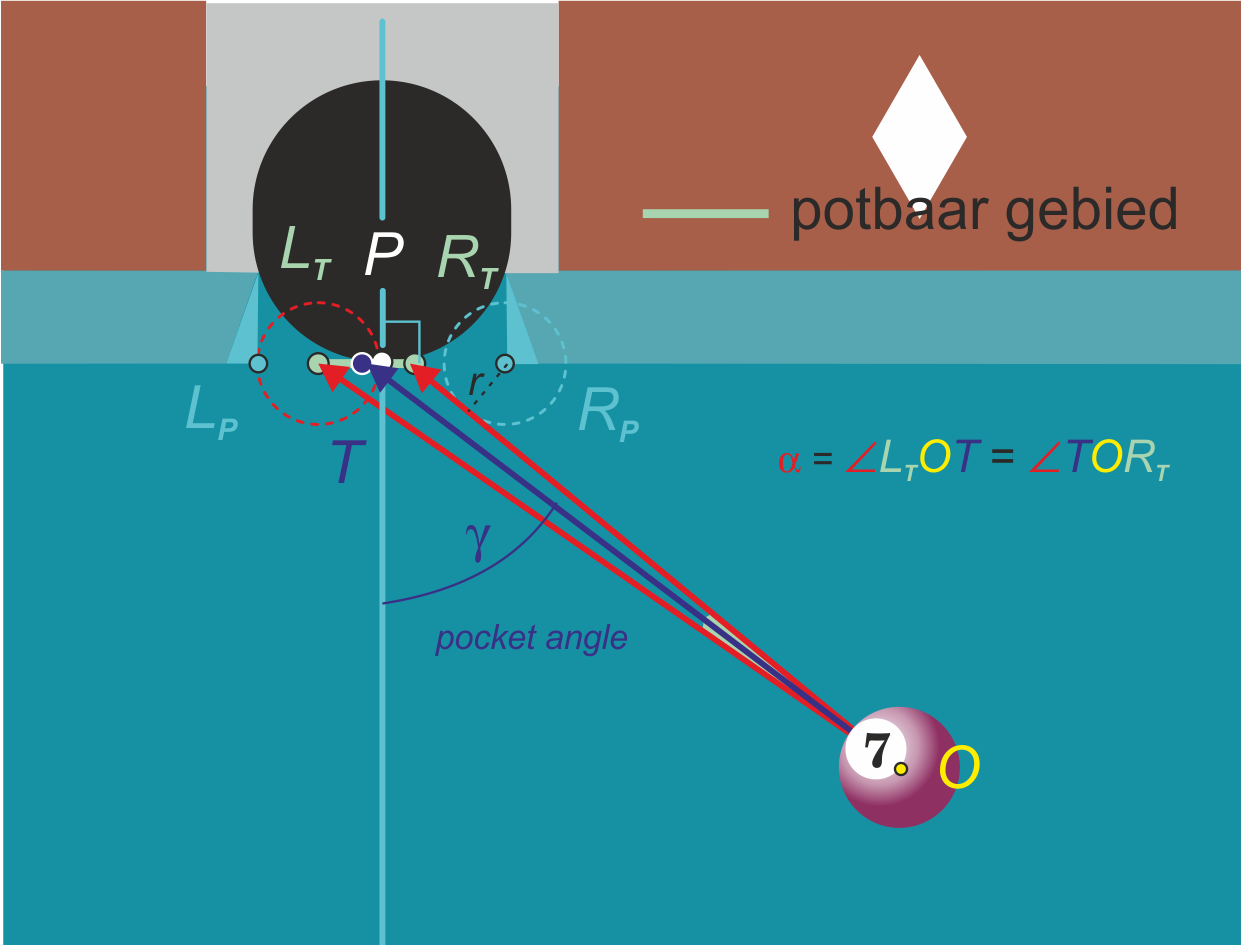
In deze paragraaf bekijken we situaties waarbij de object ball niet op de pocket centerline ligt. Zie figuur 3. Om je potkansen te vergroten kies je soms als targetline niet de lijn naar het midden van de pocket. We noemen het punt in het potbare gebied waar we op richten $T.$ We beweren dus dat om de potkans te vergroten $OP$ niet altijd gelijk is aan $OT.$
De targetline zal nu een hoek maken met de pocket centerline. De hoek tussen de targetline $OT$ en de pocket centerline noemen we de pocket angle $\gamma.$
We zien in de figuur dat het potbare gebied nu kleiner is dan $2r.$
In de eerste plaats zien we dat in dit geval geldt:
lijnstuk $L_TP = r.$ En voor $R_TR_P$ hebben we: $\cos(\gamma)=\frac{r}{R_TR_P}.$ Oftewel $R_TR_P=\frac{r}{\cos(\gamma)}>r.$ Dus $PR_T = 2r - R_TR_P < r.$ Er geldt dus dat voor het potbare gebied $L_TR_T < 2r,$ dus kleiner dan bij $\gamma=0$ (object ball op de pocket centerline).
Opgave 3
-
Bereken de uiterste hoek waaronder je een object ball naar het midden $P$ van de pocket kunt spelen. Zie figuur 4.
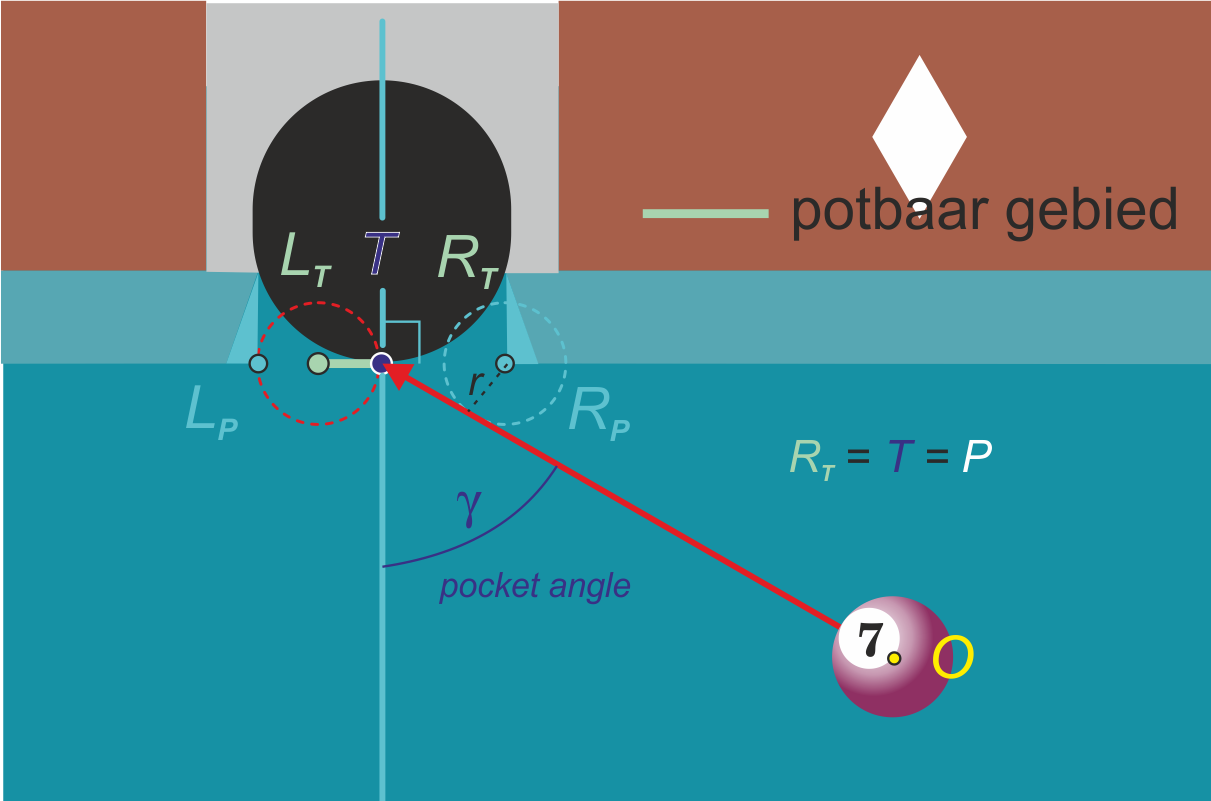
Figuur 4 -
Leg uit dat het potbare gebied nu gehalveerd is.
Willem beweert dat punt $T$ nu op het midden van lijnstuk $L_TP$ gekozen moet worden om de grootste potkans te krijgen.
-
Leg uit of hij gelijk heeft.
Opgave 4
Wat is de grootste pocket angle $\gamma$ waarover een object ball naar het potbare gebied te spelen is (figuur 5)? De foutmarge is dan $0.$
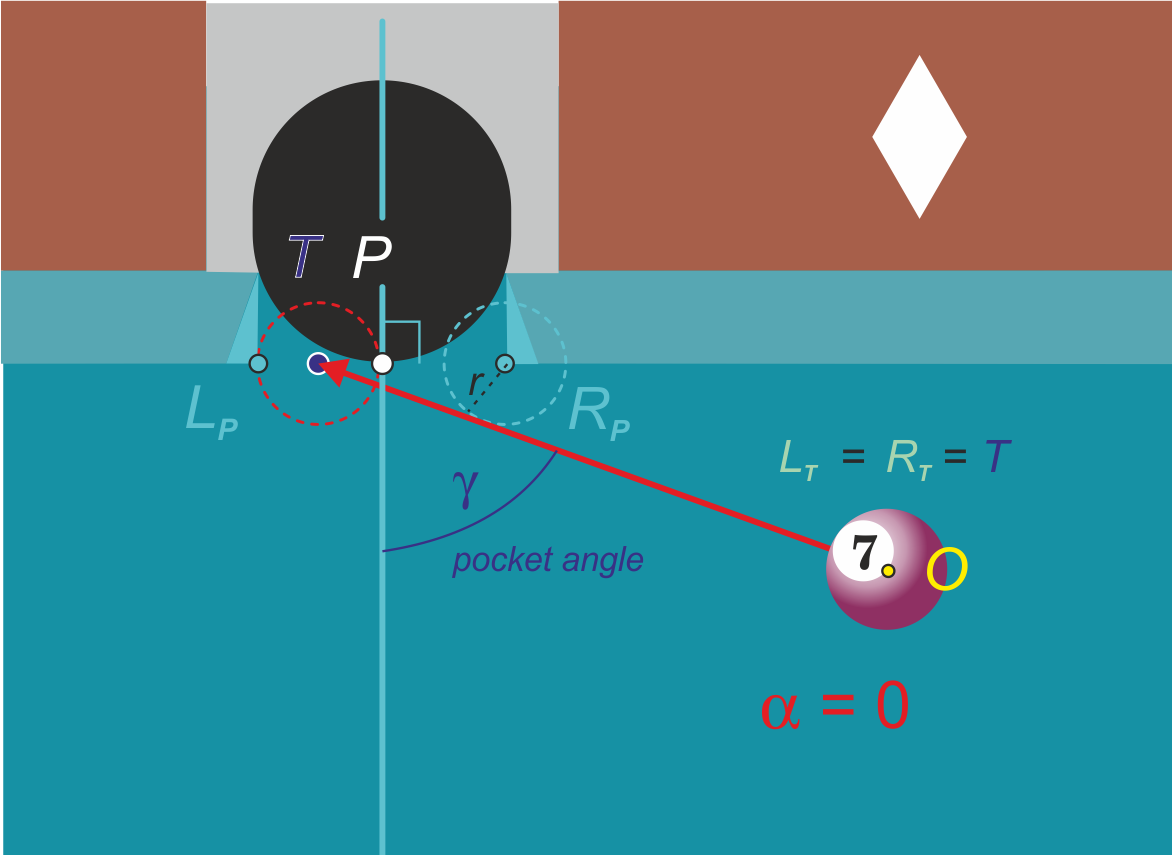
Botsingen aan de hoeken van de pocket
Het kan natuurlijk iets beter dan in opgave 4 door de pocket angle iets groter te maken, de object ball langs $R_P$ te laten scheren en op $L_P$ te laten botsen. Dan ligt het middelpunt van de bal nog iets onder de lijn $L_PR_P.$ Maar omdat een component van de impuls, de pocket in gericht, behouden blijft en niet omgekeerd wordt bij de botsing, is het mogelijk dat de bal alsnog over de lijn $L_PR_P$ komt en de pocket in rolt. Het is niet eenvoudig te berekenen wat nu echt de maximale hoek is en we laten het bij deze kwalitatieve opmerkingen.
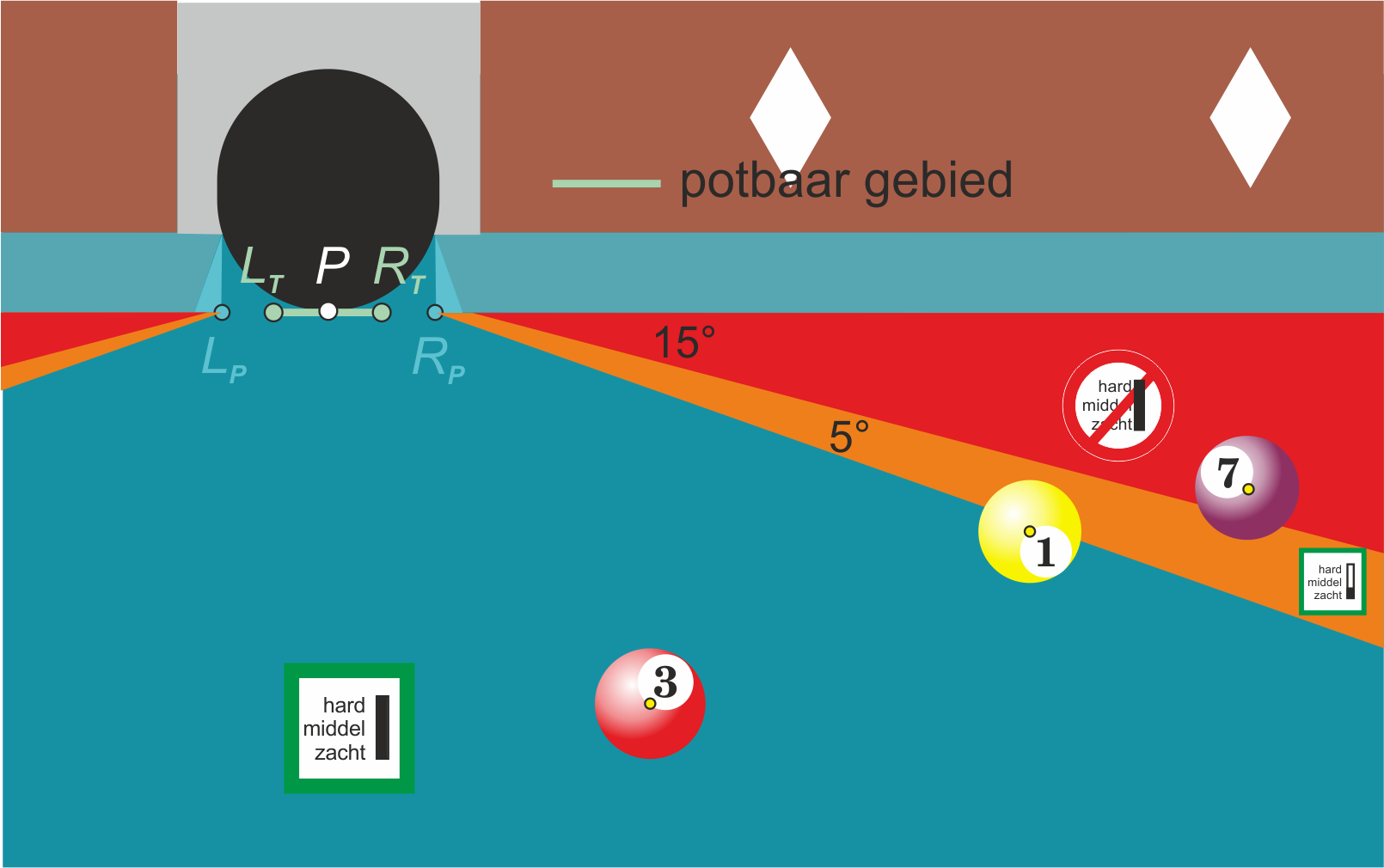
Op basis van de resultaten uit de vorige opdrachten kunnen we bij benadering nu stellen dat:
- een object ball onmogelijk te potten is wanneer hij (deels) in het gebied tussen de band en $15^{\rm o}$ van de band af ligt (zoals de 7-ball in het rode gebied in figuur 6);
- een object ball te potten is op lage snelheid, wanneer hij (deels) in het gebied tussen de $15^{\rm o}$ en $20^{\rm o}$ van de band ligt (zoals de 1-ball in het oranje gebied);
- vanuit het groene gebied een object ball direct potbaar is (zoals de 3-ball)
In de figuur zie je in de symbolen of je een bal zacht moet spelen of dat het ook iets harder of zelfs hard mag. Bij hard spelen worden de banden en hoeken van pockets verder ingedrukt tijdens de botsing. Dan geldt niet meer de regel: hoek van inval is gelijk aan hoek van terugkaatsing.
Straight shot: object ball op verschillende plaatsen tussen cue ball en pocket
In deze paragraaf bekijken we het geval dat de cue ball, de object ball en de pocket op één lijn liggen. Dan zijn er twee simpele gevallen waarbij je de object ball vrijwel zeker kunt potten. Ten eerste het geval dat de object ball vlak voor de pocket ligt. Dan moet je wel erg slecht stoten om deze niet te potten. Maar ook het geval waarbij de cue ball (vrijwel) tegen de object ball aan ligt en de verbindingslijn van de middelpunten samenvalt met de pocket centerline. Na de ‘botsing’ van cue ball met de object ball kan de laatste alleen maar langs de pocket centerline de pocket in rollen.
Uit deze twee opmerkingen lijkt te volgen dat als de object ball ergens tussen de cue ball en de pocket in ligt, het wel eens moeilijker zou kunnen zijn om de object ball te potten: afhankelijk van hoever de object ball van de pocket ligt, mag een speler een maximale fout van $\beta$ hebben om de object ball te kunnen potten. Met andere woorden: die $\beta$ hangt af van de afstand $d.$ We stellen ons dan ook de vraag: op welke plaats tussen de cue ball en de pocket is het potten van de object ball het moeilijkst? Zie figuur 7.
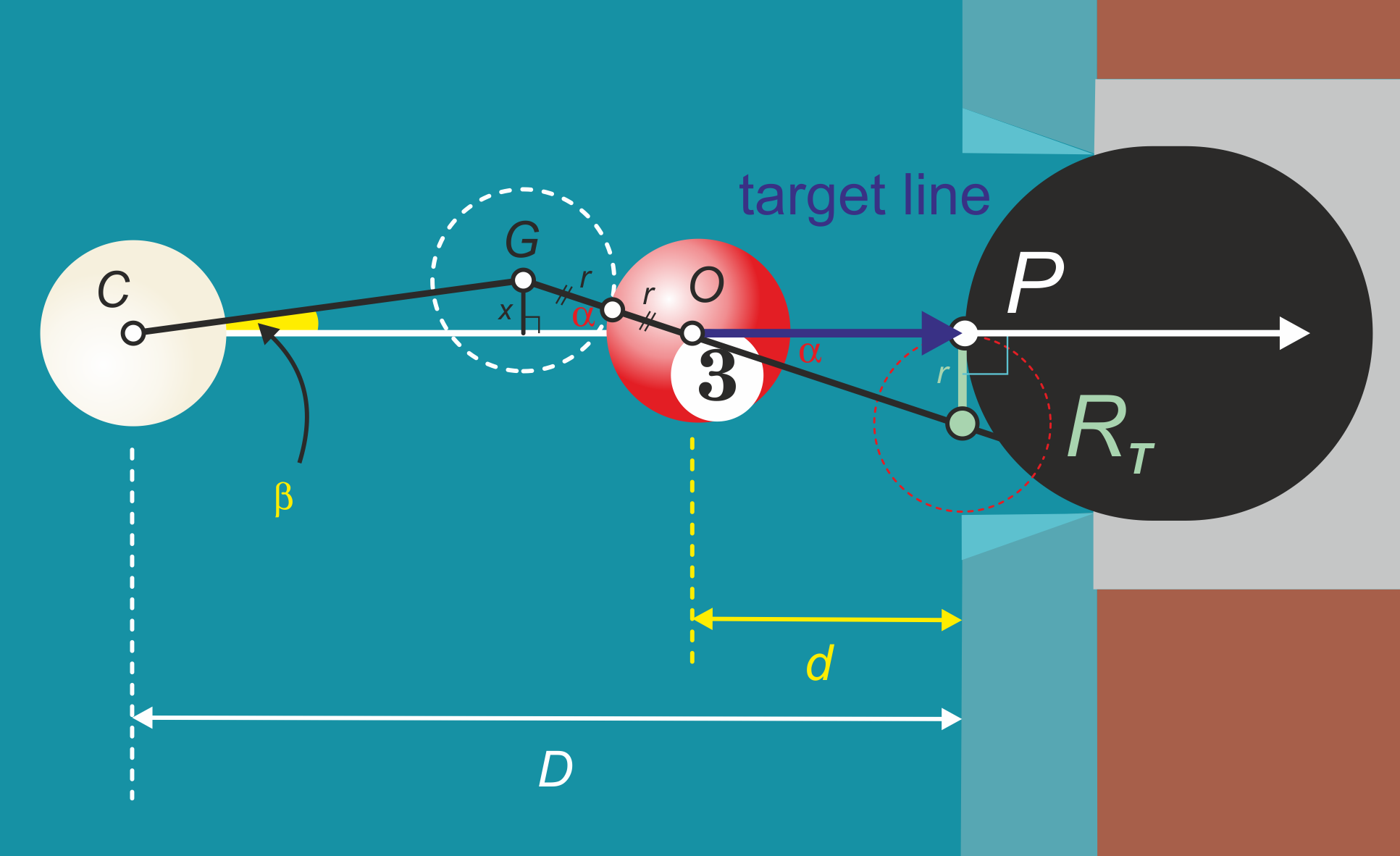
Bij het afstoten van de cue ball maakt de speler een gemiddelde fout van $\beta.$ De cue ball botst dan op de object ball, die vervolgens onder een kleine hoek $\alpha$ richting pocket rolt. Voor de maximaal toelaatbare afwijking vanaf het midden van de pocket nemen we weer $r$ (de object ball ligt in dit voorbeeld dus op de pocket centerline).
Omdat we veronderstellen dat we met een geoefende speler te maken hebben, mogen we aannemen dat in een groot gebied tussen cue ball en pocket geldt dat de hoeken $\alpha$ en $\beta$ klein zijn. Wanneer hoeken klein zijn geldt $\sin(t) \approx t$ en $\tan(t) \approx t$ $(t$ is hier in radialen en niet in graden, $2\pi$ radialen = $360^{\rm o}).$
Opgave 5
De fout $\beta$ zorgt ervoor dat de ghost ball ($G$ in figuur 7) een stukje naast de target line komt, en wel met een afstand $x.$
-
Toon aan dat in de figuur bij benadering geldt dat $x=\frac{2r^2}{d}.$
Omdat we hadden vastgesteld dat de maximale fout $\beta$ afhangt van de afstand d tot de pocket (in figuur 7), kun je schrijven $\beta(d).$
-
Toon met 5a) aan dat bij benadering geldt dat $\beta(d) =\frac{2r^2}{d(D-d-2r)}.$
Opgave 6
Toon, door de zojuist gevonden formule te differentiëren en gelijk te stellen aan $0,$ aan dat er een minimale waarde is voor $\beta$, als de object ball ruwweg ligt midden tussen de cue ball en de pocket: $d=\frac{D}{2}-2r\approx \frac{D}{2},$ met $r\ll D$.
Wanneer de object ball ongeveer halverwege de cue ball en de pocket ligt, is de hoek $\beta$ minimaal om de object ball nog net binnen het potbare gebied te krijgen. En een kleinere toegestane waarde van $\beta$ maakt een stoot moeilijker. Deze bal is dus het moeilijkste te potten.
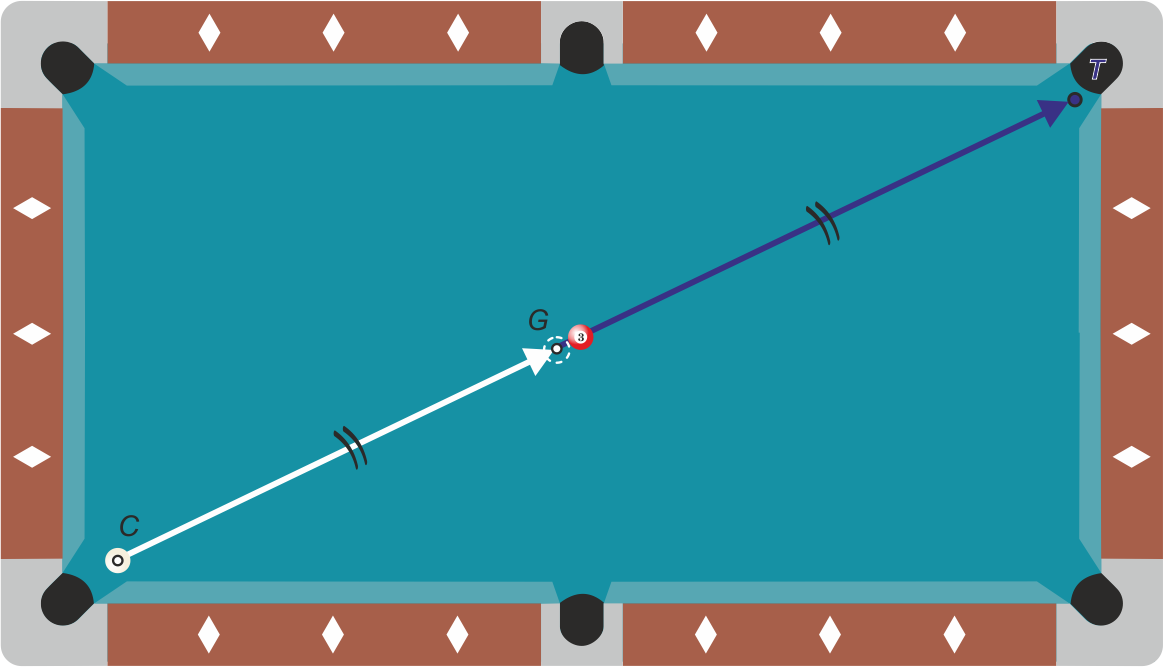
In figuur 8 zie je het shot waarbij $D$ het langst is en die het moeilijkst te potten is.
Opgave 7
Willem beweert dat de door de speler maximaal toegestane fout ($2\beta$) bij dit shot, kleiner is dan $1^{\rm o}.$
Onderzoek, met behulp van de formule van opgave 5b, of hij gelijk heeft. Neem hierbij $D = 280$ cm en $r = 3$ cm.
Nu je wat meer weet over het potbare gebied van een pocket en de foutmarges, begrijp je wellicht beter hoe je de moeilijkheid van een shot kunt bepalen. Je hebt gezien of kunnen berekenen dat:
- de foutmarge van een shot langer dan $100$ cm minder dan $3{,}5^{\rm o}$ is;
- de moeilijkste shots die zijn waarbij de object ball midden tussen de cue ball en de pocket ligt;
- je de potkans kunt vergroten door op een deel van een pocket te richten.
Hopelijk begrijp je weer wat meer over het poolspel en ga je proberen het in praktijk te brengen. Wanneer het erg goed gaat aan de smartpooltafel, probeer dan ook eens een wedstrijdtafel (9ft).
Het komende artikel zal ik wat uitleg geven over de baan van de cue ball na contact met de object ball en wat de hoogte van de tippositie (plek waar je de cue ball raakt) daar aan invloed op kan hebben.
Wiskunde bij poolbiljarten:
|
