Bij het poolbiljarten is er één bal die je met de keu in beweging mag brengen (stoten). Die bal noemen we de cue ball (stootbal). Daarmee moet je een andere bal (object ball genaamd) in een gat (pocket) in de biljarttafel stoten (potten).

De ghost ball

Wat gebeurt er wanneer een cue ball een object ball raakt? Zie het bovenaanzicht in figuur $1$. Je stoot bijvoorbeeld de cue ball vanaf middelpunt $C$ in de richting aangegeven in figuur $1a$. In figuur $1b$ is het moment aangegeven waarop de cue ball de object ball raakt. Het middelpunt van de object ball noemen we $O$ en van de cue ball op dat moment $G$. In figuur $1c$ is de richting van de object ball na de botsing aangegeven met een zwarte pijl.

 

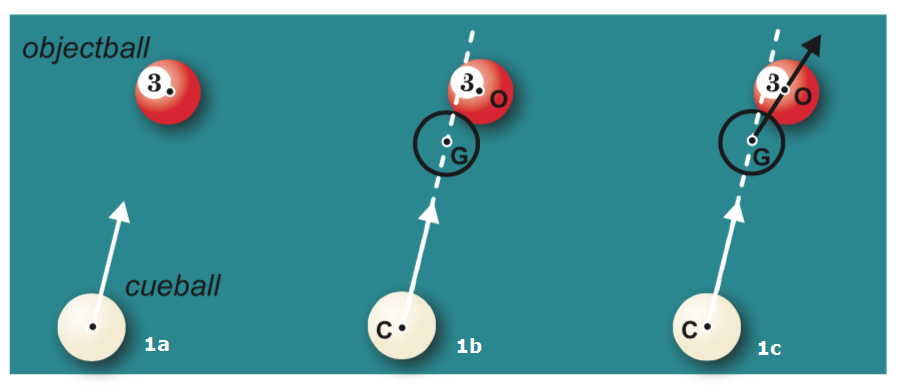
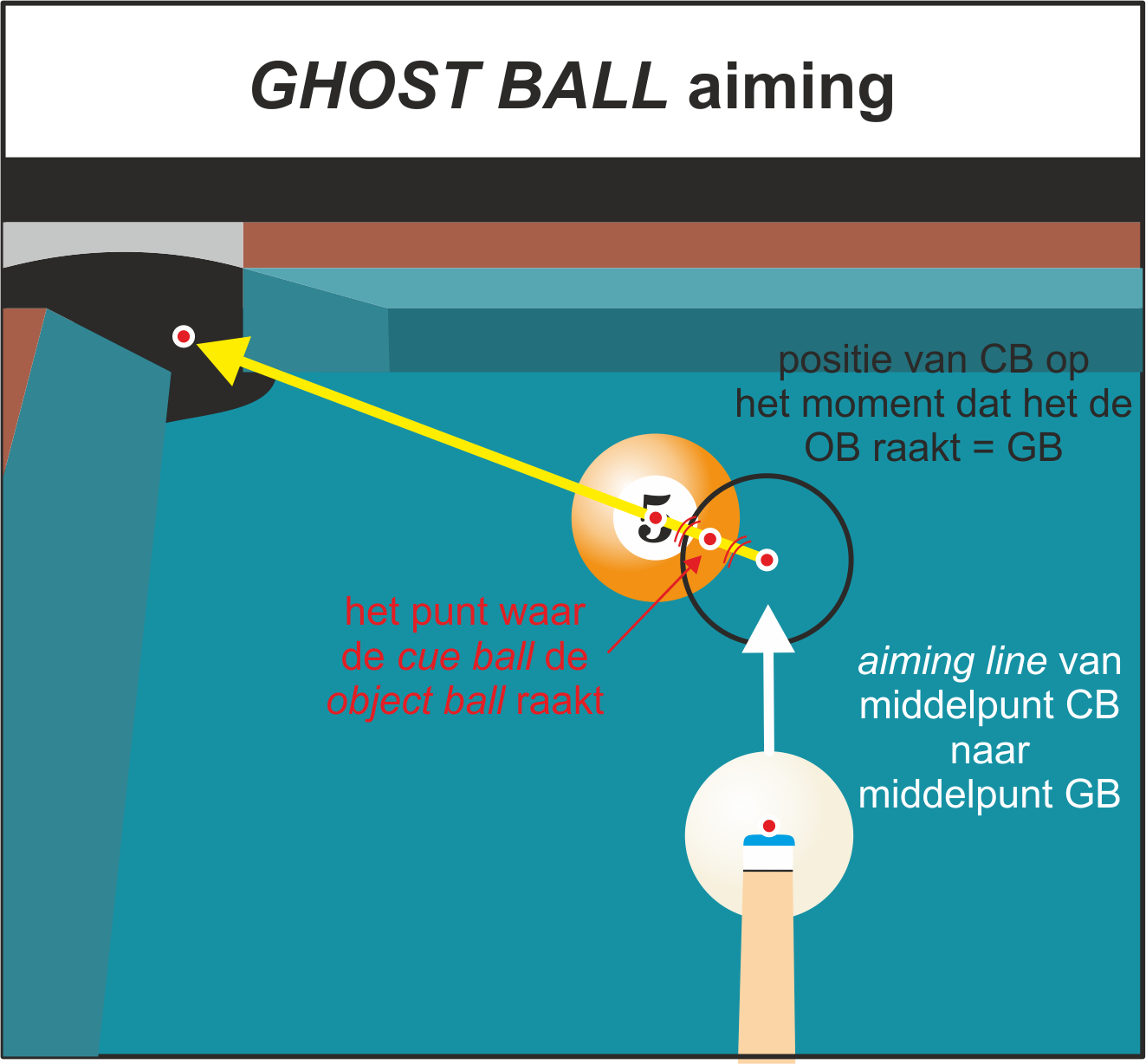
De cue ball op het moment van raken, noemen we ghost ball. De ghost ball en de object ball hebben één punt gemeenschappelijk, dat noemen we het raakpunt. Dat punt ligt op lijnstuk $OG$. Zie ook figuur $2$, waarin te zien is hoe het er vanuit het oogpunt van de speler uitziet.

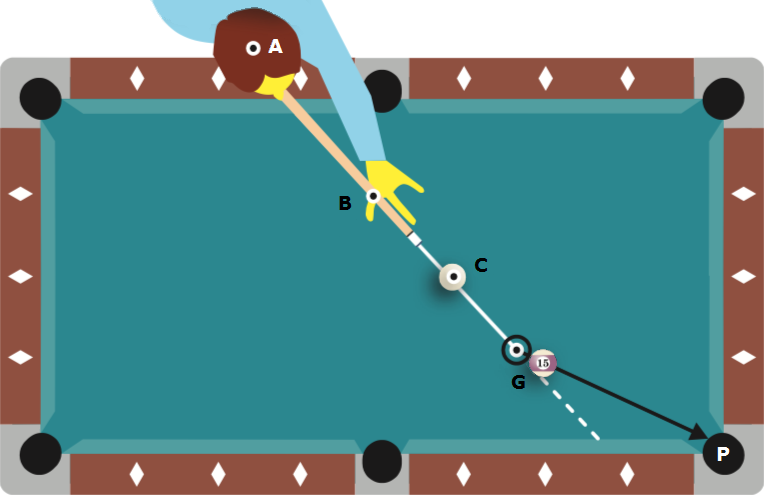
De richting waarin je stoot ($CG$) wordt de aim line. Om de cue ball te spelen zal de keu in lijn van $CG$ moeten liggen. Hiervoor zullen je voorhand, arm en hoofd ook in dezelfde lijn moeten liggen zoals in het bovenaanzicht in figuur $3$. 

De hoek tussen de aim line $CG$ en de richting waaronder de object ball vertrekt $GO$ noemen we de hoek waaronder een object ball wordt geraakt. Zie ook figuur $4$.

 

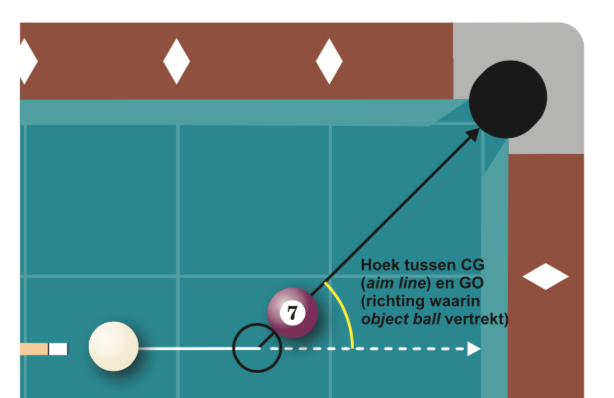
De volheid (gedeelte overlap) waarmee de cue ball deze object ball raakt bepaalt de hoek waaronder de object ball vertrekt.
We noemen een bal vol wanneer het middelpunt van de cue ball in de richting van het middelpunt van de object ball gestoten wordt.

Opgave 1

a)    Is het mogelijk om de object ball over dezelfde lijn te laten vertrekken als de cue ball?

b)    Wat is de grootste hoek waaronder de object ball kan vertrekken?

c)    Wanneer de cue ball de object ball voller raakt, zal de hoek waaronder de object ball vertrekt dan kleiner of groter zijn?

d)    Wanneer de cue ball de object ball voller raakt, zal de snelheid waarmee de object ball vertrekt dan lager of hoger zijn?

 

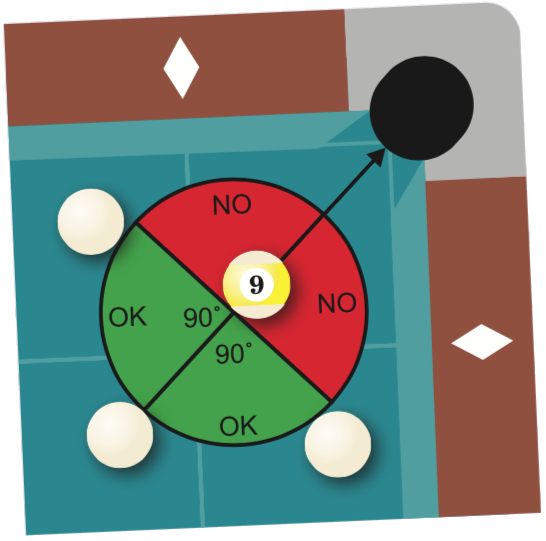
Wel of niet te potten?

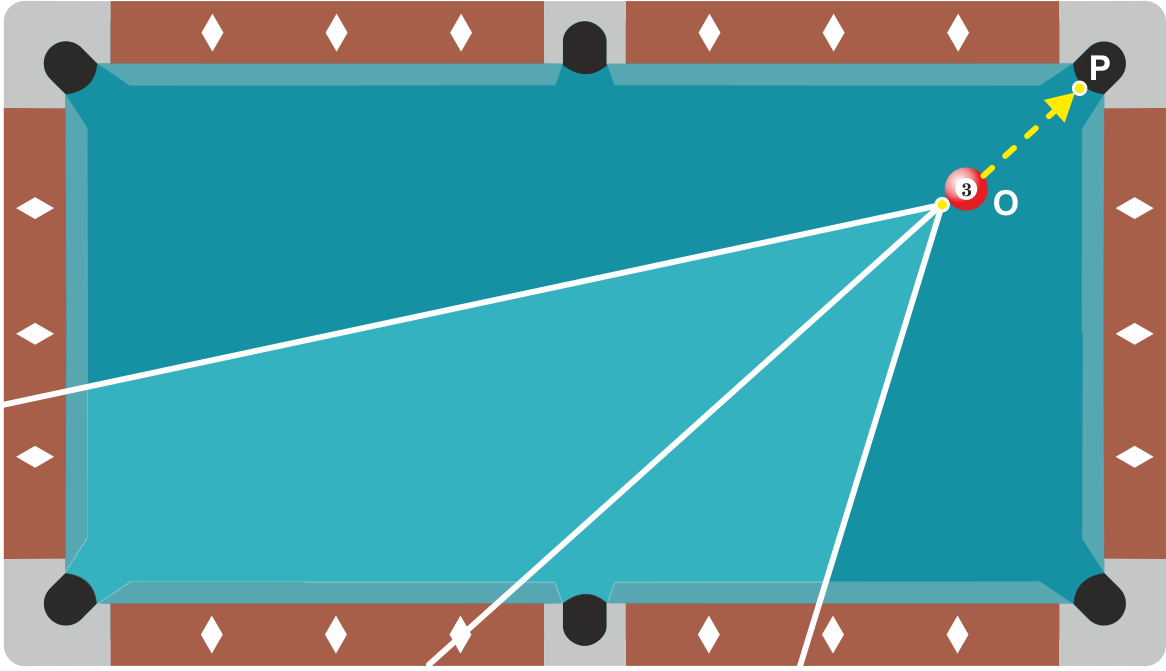
Elke object ball die een vrije baan heeft naar een pocket is te potten, maar niet vanuit elke hoek. In figuur $5$ is met groen aangegeven vanwaar de object ball te potten is en met rood vanwaar dat niet mogelijk is.

De grootste hoek waaronder je een bal nog kan potten is $90°$, je moet dan wel erg hard spelen om de snelheid over te brengen op de object ball. Wanneer je de object ball dunner raakt, zal deze namelijk minder snelheid meekrijgen.

 

Half vol raken

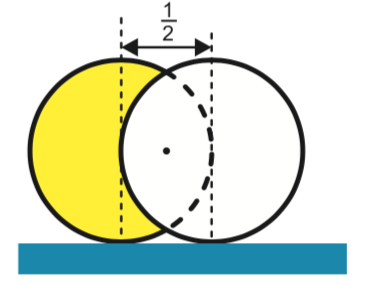
Wanneer je met de cue ball de object ball niet vol raakt, vertrekt deze onder een hoek. Figuur $6$ laat een vooraanzicht zien van een situatie waarbij de cue ball de object ball precies halfweg raakt.  

 

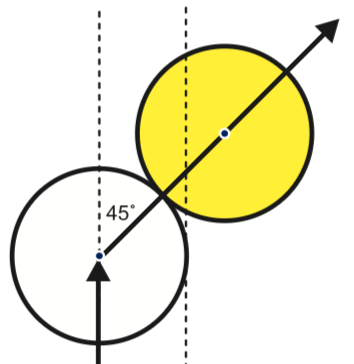
Opgave 2

Als de objectball onder een hoek van $45°$ vertrekt, was deze dan half vol geraakt?

 

 

 

 

 

 

 

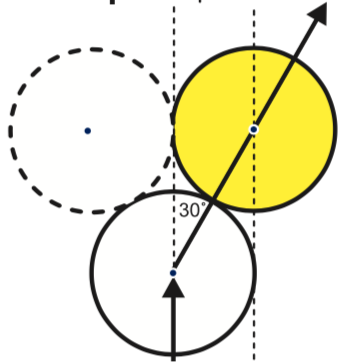
Opgave 3

In figuur $8$ zie je een bovenaanzicht van de situatie waarbij de cue ball zo gestoten wordt dat hij precies de helft van de object ball raakt (dus half vol raken). Het lijkt erop dat de hoek waaronder de object ball vertrekt $30$ graden is.
Kun je narekenen of dat zo is?

 

 

 

 

 

Het raakpunt vinden met de SPAT

Hoe vind je het goede raakpunt? Je kunt hiervoor de SmartPool Aiming Tool (SPAT) gebruiken. Leg de gele halve ring direct onder de te potten object ball, met de pijl in de richting van de pocket. Richt de cue ball op de stip in het midden van de cirkel. De object ball is potbaar zolang de lijn vanuit $C$ naar dat punt in het groene deel ligt.

 

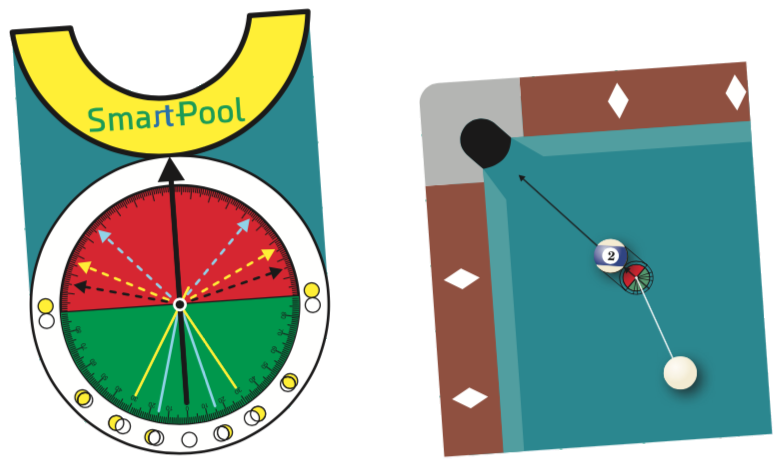
Verhouding tussen hoek en overlappend stuk.

In figuur $10$ noemen we $R$ de straal van de bal en de hoek noemen we $\phi$. Er geldt: $d + x = R$ en $d = 2R \cdot \sin(\phi)$. Het overlappende deel is $d + 2x$.

 

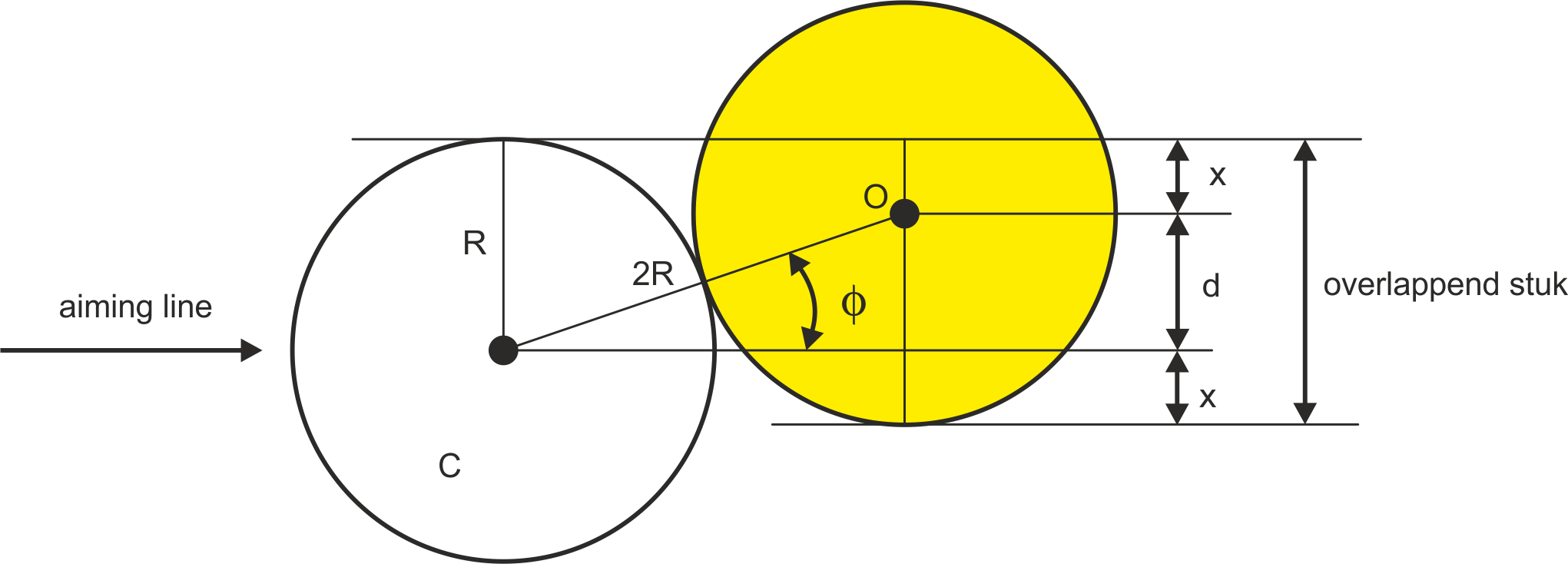
Opgave 4

Laat zien dat voor het relatieve overlappende deel geldt: $\frac{\mbox{overlappend stuk}}{\mbox{diameter}} = 1 – \sin(\phi)$

 

 

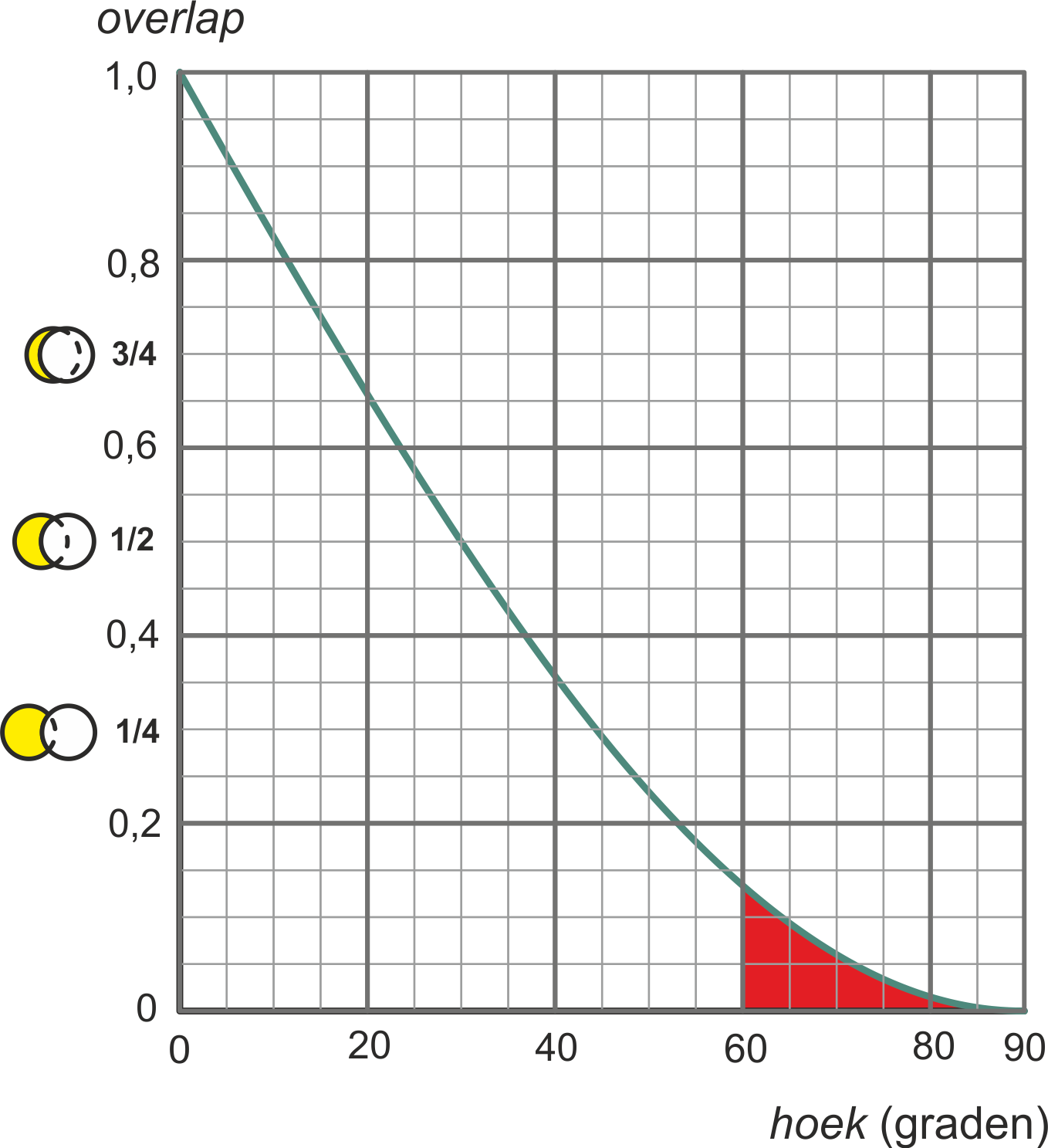
Als je in een grafiek $f(\phi) = 1 - \sin(\phi)$ bekijkt en dus de hoek waaronder je de bal moet raken op het domein $[0°, 90°]$ krijg je een deel van een sinusoïde te zien (figuur $11$).

Je kunt hierin zien dat hoeken groter dan $60°$ erg lastig zijn te richten (rood gebied). Een kleine afwijking in de overlap heeft grote gevolgen voor de hoek. 

 

 

Opgave 5

Welk deel overlap moet je raken om een object ball onder een hoek van $45°$ te laten vertrekken?

 

In het boek “Mind over Billiards” van Del Thiessen staat een tabel over de frequentie van verschillende contacten tussen de cue ball en object ball. Deze tabel is hier overgenomen in figuur $12$. De $510$ stoten van een willekeurige poolwedstrijd staan gecategoriseerd in $7$ groepen: $1/2$, $3/4$, $7/8$, $1/4$, vol, $1/8$ en feather (dun).

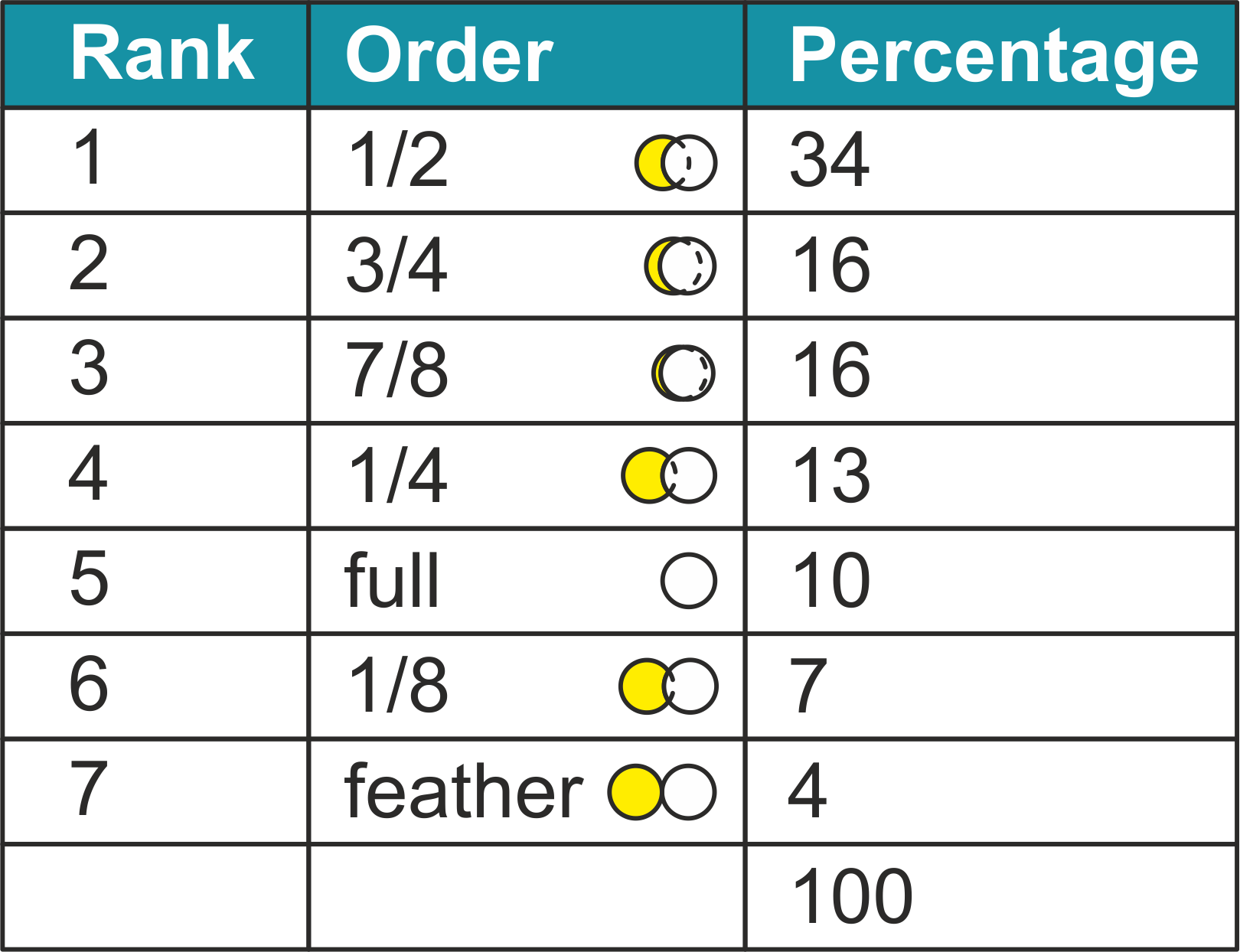
Een bal dunner dan $1/4$ deel raken gebeurt dus maar in zo’n $10\%$ van alle stoten.

Opgave 6

Bereken met behulp van de formule bij opgave $4$ de hoek waaronder de cue ball vertrekt bij de vier meest voorkomende situaties:

 

Opgave 7

Een poolspeler zal altijd proberen om binnen de $1/2$ ball hit lijnen uit te komen voor een ideale pot positie. 
Kun je dit verklaren aan de hand van de grafiek  in figuur $11$?

Opgave 8

Laat zien dat op basis van de tabel van Thiessen in ruim $75\%$ vanuit dit gebied wordt gepot.
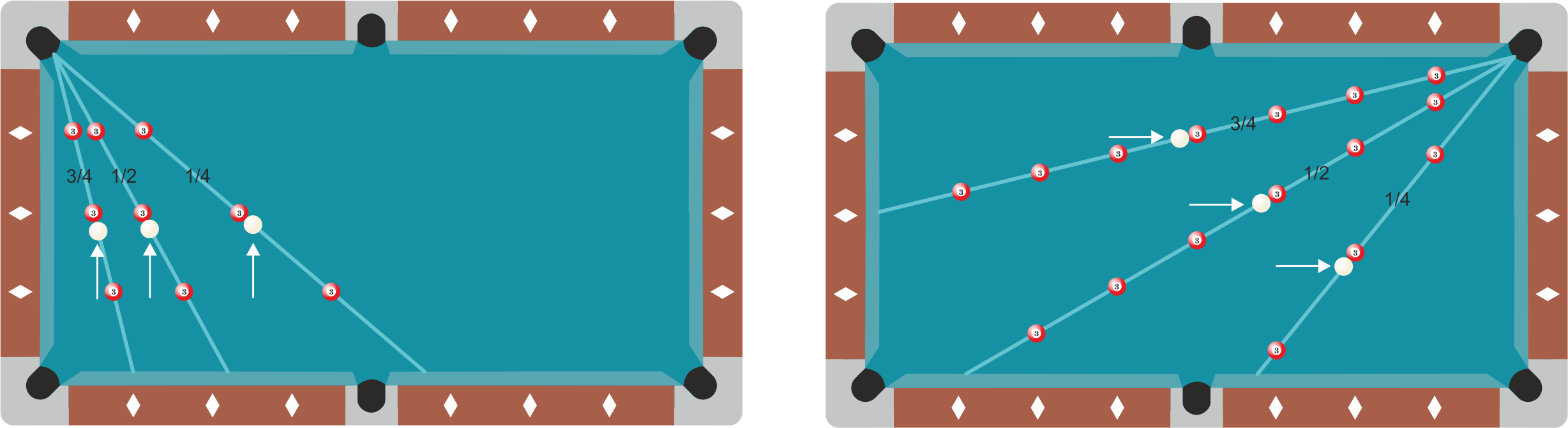
Teken in figuur $13$ de $¾$ en $¼$ lijn erbij.

 

Oefeningen aan tafel

Het is belangrijk om te oefenen met de vaakst voorkomende situaties. Dit kan je doen door de object ball onder een hoek van $15$, $30$ of $45$ graden met de korte of lange band te leggen en de cue ball evenwijdig aan die band te spelen (zie figuur $14$). Door steeds de juiste plek te zoeken om de cue ball neer te leggen train je je hersenen om de belangrijkste hoeken te herkennen en zal je potvermogen toenemen. 
In het volgende artikel zal ik wat uitleg geven over het bandenspel. Ik wens jullie veel poolplezier!

 

 

Smartpool “Wiskunde aan de pooltafel”

Erik van Haren heeft een werkboekje geschreven naar aanleiding van de vraag vanuit de KNBB om de pooltafel als middel in te zetten om wiskundige vragen te beantwoorden. Bij het doorwerken van het boekje zul je interessante wiskunde tegenkomen en tegelijkertijd veel leren van het poolspel. Met de bijgeleverde SPAT heb je een hulpmiddel in handen om de theorie in de praktijk toe te passen.

Het boekje is te koop via www.smartpool.nl en www.mathplay.nl 

Voor Pythagoras-lezers is het boekje met korting te bestellen. Door bij de bestelling van een boekje de actiecode pythpool te vermelden, ontvang je het boekje inclusief SPAT en verzendkosten voor € 4,95 i.p.v. € 7,25.

 

 

Wiskunde bij poolbiljarten: Een introductie Het goede punt raken Via de band in de pocket Diverse moeilijkheden bij het potten De baan van de Cue ball

Bekijk oplossing