Sangaku
Sangaku is een Japans woord dat "wiskundig tablet" betekent. Het is de naam die werd gegeven aan kleurrijke tabletten van hout waarop wiskundige tekeningen afgebeeld stonden. Sangaku's werden opgehangen in de buurt van Shinto- of Boeddhistische tempels. Het Pythagoras-archief biedt een goed historisch overzicht.
Ik stel me voor dat een tempel een gevoel voor het hoogste goed opriep, het zien van de tabletten een ervaring van schoonheid, en de boodschappen op de tabletten een verlangen naar waarheid. Zo’n combinatie is enigszins te vergelijken met glas-in-lood ramen in kathedralen, of meetkundige versieringen in moskeeën. Maar hier is nog iets meer te vertellen. Op de tabletten stonden namelijk wiskundige stellingen of problemen zonder bewijs of antwoord en de aanschouwer werd uitgenodigd om het bewijs of antwoord te vinden. Mensen van alle rangen en leeftijden deden mee en aangezien die uitnodiging nooit ingetrokken werd kunnen wij dat ook doen. Daarvoor heb ik vier voorbeelden gekozen. Deze vier voorbeelden komen van een Engelstalige website. Om ze wat toegankelijker te maken heb ik ze vertaald naar het Nederlands en er wat hints bijgegeven mocht dat nodig zijn.
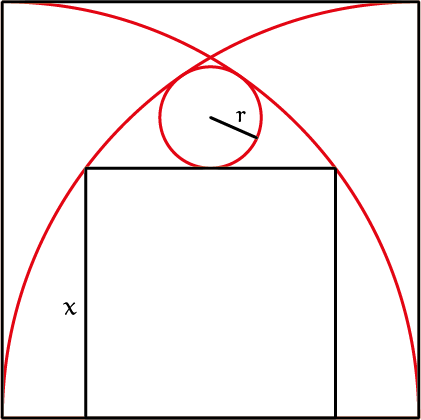
Sangaku 1De lengte van de zijden van het grote vierkant is $1$. De kwartcirkels, het kleine vierkant en de kleine cirkel raken elkaar in één punt. Bereken de lengte van zijde $x$ van het kleine vierkant en de straal $r$ van de kleine cirkel.
|
Sangaku 2De drie cirkels raken elkaar en de rechte lijn in één punt. De drie cirkels hebben middelpunten $c_1$, $c_2$ en $c_3$ en stralen $r_1$, $r_2$ en $r_3$. Laat zien dat $$\frac{1}{\sqrt{r_2}}=\frac{1}{\sqrt{r_1}}+\frac{1}{\sqrt{r_3}}.$$
|
Sangaku 3Het vierkant heeft zijden van lengte $4$ en de twee schuine lijnen zijn raaklijnen aan beide kleine cirkels en aan de halve cirkel. Bewijs dat de verhouding tussen de stralen van de twee kleine cirkels gelijk is aan $3 : 2$.
|
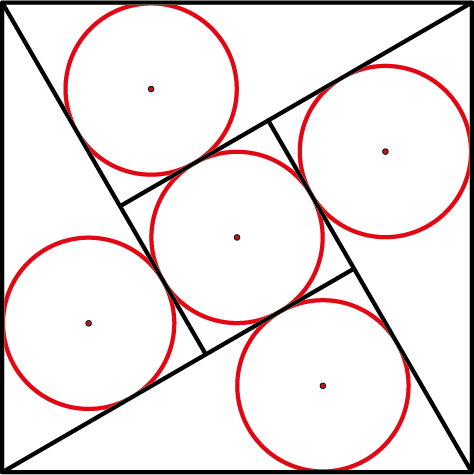
Sangaku 4Het grote vierkant heeft zijden van lengte $1$. Het is gevuld met een vierkant en vier congruente rechthoekige driehoeken met hun ingeschreven cirkels. Hoe groot is de straal van de cirkels als ze allemaal gelijk zijn?
|
Enkele hints voor het oplossen van de sangaku's vind je onder de knop [Bekijk oplossing] onderaan de pagina.
HandigDe volgende cirkeleigenschappen, die je wellicht al kent, zijn nuttig.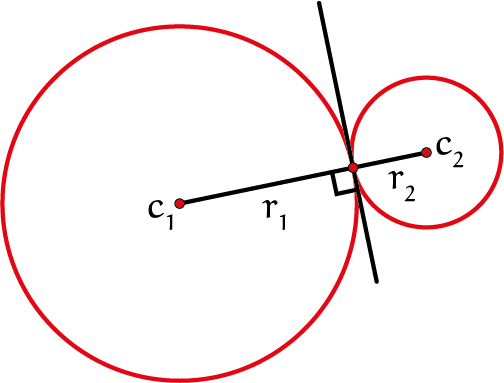
|
In de onderste figuur zijn drie raaklijneigenschappen te zien. Het middelpunt van de cirkel is $C$ en de hoeken op de raakpunten van $A$ en $B$ zijn beide $90^{\rm o}$. De raaksegmenten $AP$ en $BP$ zijn even lang en de hoeken $\alpha$ en $\beta$ hebben een som van $180^{\rm o}$. Deze eigenschappen zijn makkelijk te bewijzen.
Bronnen |
||||
|
||||
Bekijk oplossing
