Twee schaatsers gaan $3\ 000$ meter schaatsen op een $400$ meterbaan. Ze beginnen een halve ronde voor de finishlijn en rijden dan nog $7$ complete ronden. De schaatsers hebben elk een eigen opbouw van de race. De een heeft de 'vlieg erin'-strategie: zo hard mogelijk beginnen en kijken waar het schip strandt. De andere schaatser kiest voor de voorzichtige aanpak: de eerste $5{,}5$ ronden iets inhouden en met de energie die hij dan nog over heeft de laatste twee ronden zo snel mogelijk schaatsen.

De rondetijden van de schaatsers staan in de tabel. De vraag is: wie wint? Wie haalt wie waar in? Hoe maak je dat inzichtelijk met een grafiek?

	Vlieg erin	Voorzichtig
$0\ m$	$0{,}0$	$0{,}0$
$200\ m$	$18{,}8$	$20{,}0$
$600\ m$	$28{,}0$	$31{,}2$
$1000\ m$	$29{,}0$	$31{,}2$
$1400\ m$	$30{,}0$	$31{,}2$
$1800\ m$	$31{,}0$	$31{,}2$
$2200\ m$	$32{,}0$	$31{,}2$
$2600\ m$	$33{,}0$	$30{,}0$
$3000\ m$	$34{,}0$	$28{,}8$

We beginnen er maar eens mee de cijfers recht-toe-recht-aan in een grafiek te zetten in figuur 1. De afstand langs de horizontale as en de rondetijden langs de verticale as. De grafiek laat zien dat de rondetijden van 'vlieg erin' oplopen, van 'voorzichtig' aan het eind naar beneden gaan.

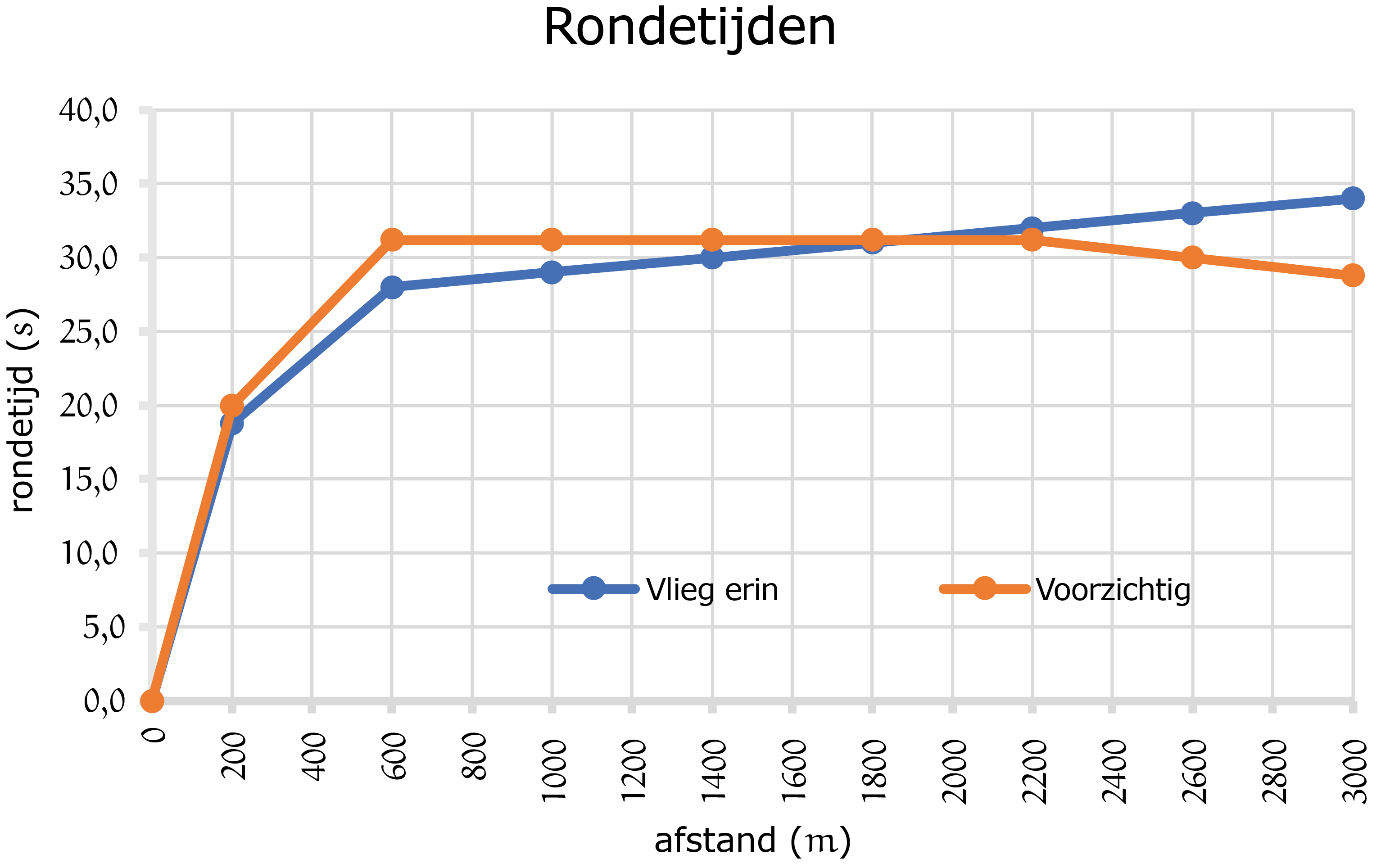
Vraag

Als je goed kijkt zie je dat bij $1800\ m$ de lijnen elkaar snijden. Wat is de betekenis van dat snijpunt? 

Het antwoord volgt gelijk, denk eerst even na vóór je verder leest!

Zie ook de tabel. De rondetijd stijgt tussen $1800\ m$ van $2000\ m$ van 'vlieg erin' van $31$ naar $32$ seconden. De snelheid daalt dus in die ronde van $12{,}9\ m/s$ naar $12{,}5\ m/s$. De snelheid van 'voorzichtig' is in deze fase $31{,}2\ s$, wat overeenkomt met $12{,}8\ m/s$. Bij het snijpunt is de snelheid van de twee schaatsers dus gelijk. De gelijke snelheden worden bereikt na dezelfde afstand, maar niet na dezelfde tijd. De schaatser 'voorzichtig' wordt op dat moment dus niet ingehaald, maar heeft vanaf dat moment wel een hogere snelheid. 

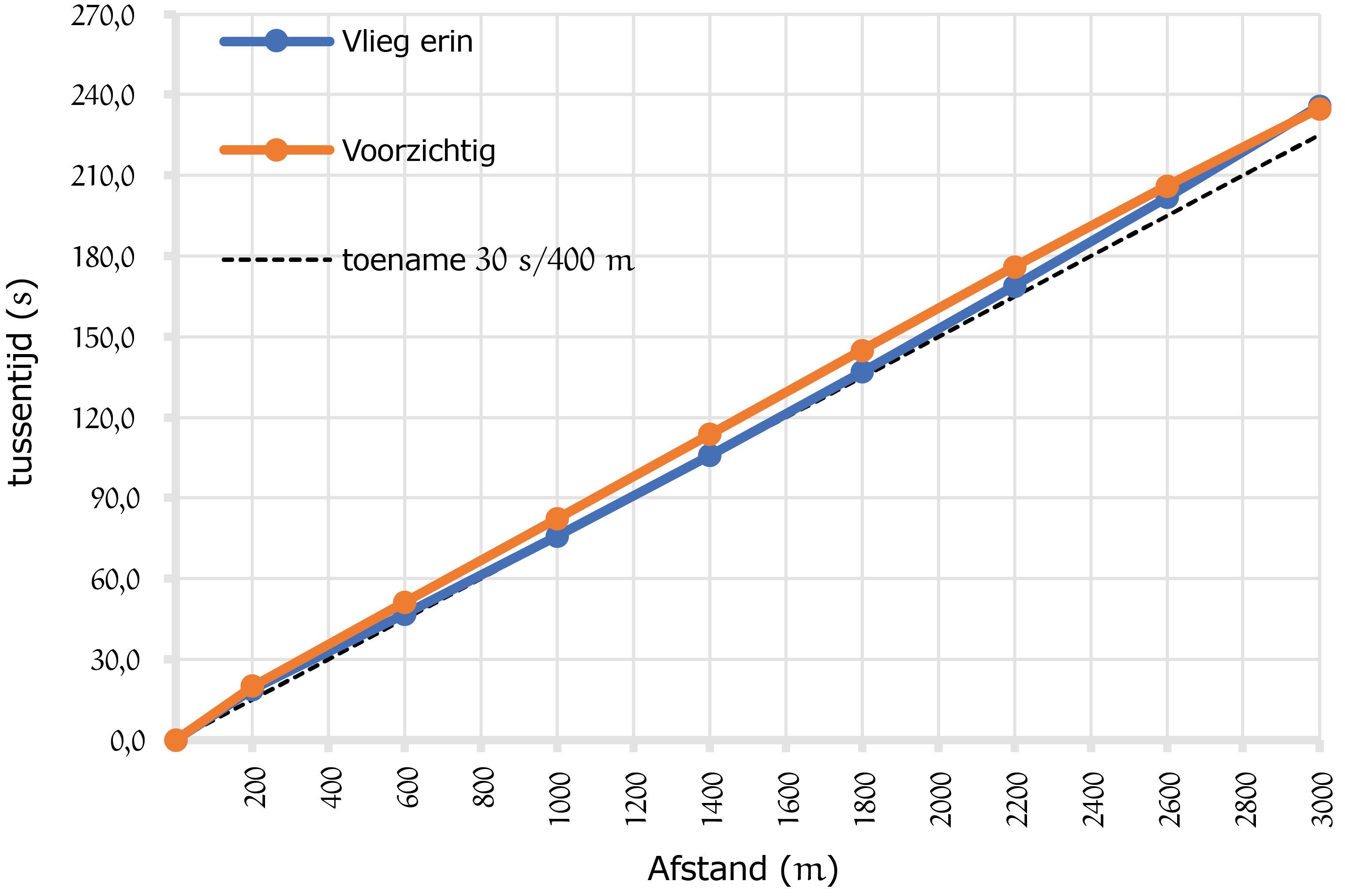
Maar wie is het snelst? En wie haalt wie waar en wanneer in? Daarvoor zullen we de rondetijden moeten optellen om zo tussentijden en eindtijden te berekenen. We zien in figuur 2 wat dat voor een grafiek oplevert. 

Helaas levert dit niet zo'n interessant plaatje op. We zien dat beide schaatsers er ongeveer 240 seconden over doen, dat is ongeveer vier minuten. Zo zie je maar weer: de verschillen in de sport zijn vaak klein, en in deze grafiek helaas ook nauwelijks af te lezen. Toch ligt hier de sleutel naar hoe je de verschillen wel inzichtelijk kunt maken. Want wat gebeurt er als je van alle grafieken dezelfde toename gaat afhalen? Met andere woorden: als je  verschilgrafieken gaat tekenen. Bij een verschilgrafiek trek je bij elke '$x$-waarde' de '$y$-waarden' van twee grafieken van elkaar af. En laten we daarvoor in dit geval de zwart gestippelde lijn uit figuur 2 nemen. Deze lijn gaat door het ene na het andere roosterpunt. De toename is dus $30\ s$ per $400\ m$. De gestippelde lijn ligt ook onder
de twee gekleurde lijnen. 

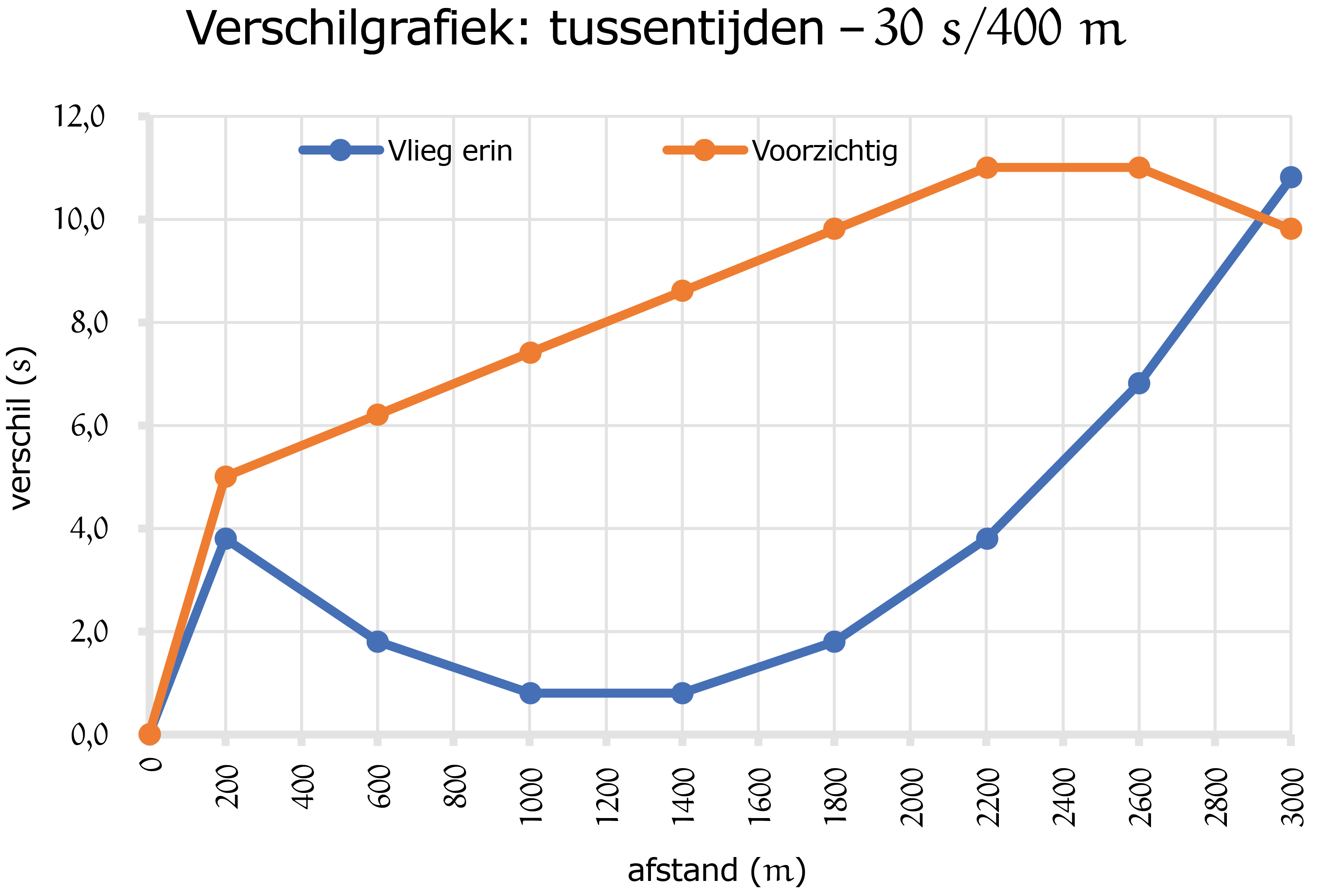
In figuur 3 is die zwarte stippellijn nu als het ware de horizontale as geworden. De verschillen worden nu zichtbaar en we zien precies wat er gebeurt!

De schaatser met de strategie 'vlieg erin' bouwt tot $1800\ m$ een tijdsverschil op van zo'n $8$ seconden met de andere schaatser. Daarna slinkt de voorsprong. En net voor de finish wordt hij door 'voorzichtig' ingehaald. Voorzichtig wint met ongeveer $1$ seconde verschil.

De grafiek valt nog interessanter te maken door er informatie aan toe te voegen: zo wordt het een echte schaatsgrafiek. We maken de stippen wat groter en zetten er de bijbehorende rondetijd in, zoals te vinden in de tabel. De getallen langs de horizontale as breiden we uit met de bijbehorende 'tussentijden' volgens de zwart gestippelde lijn (uit figuur 2), zo zie je hoeveel tijd er van de tussentijden van de schaatsers is afgehaald. En in de legenda voegen we de eindtijden van de schaatsers toe, daar gaat het uiteindelijk om.

We gaan de grafiek ook wat rustiger maken door overbodige info en elementen eruit te halen. De startinfo van de schaatsers ($0$ meter afgelegd na $0$ seconden) halen we eruit. Deze 'nulinfo' voegt niets toe. En ook de verticale lijnen hebben voor de afleesbaarheid eigenlijk geen functie. De stippen staan immers al netjes onder elkaar.

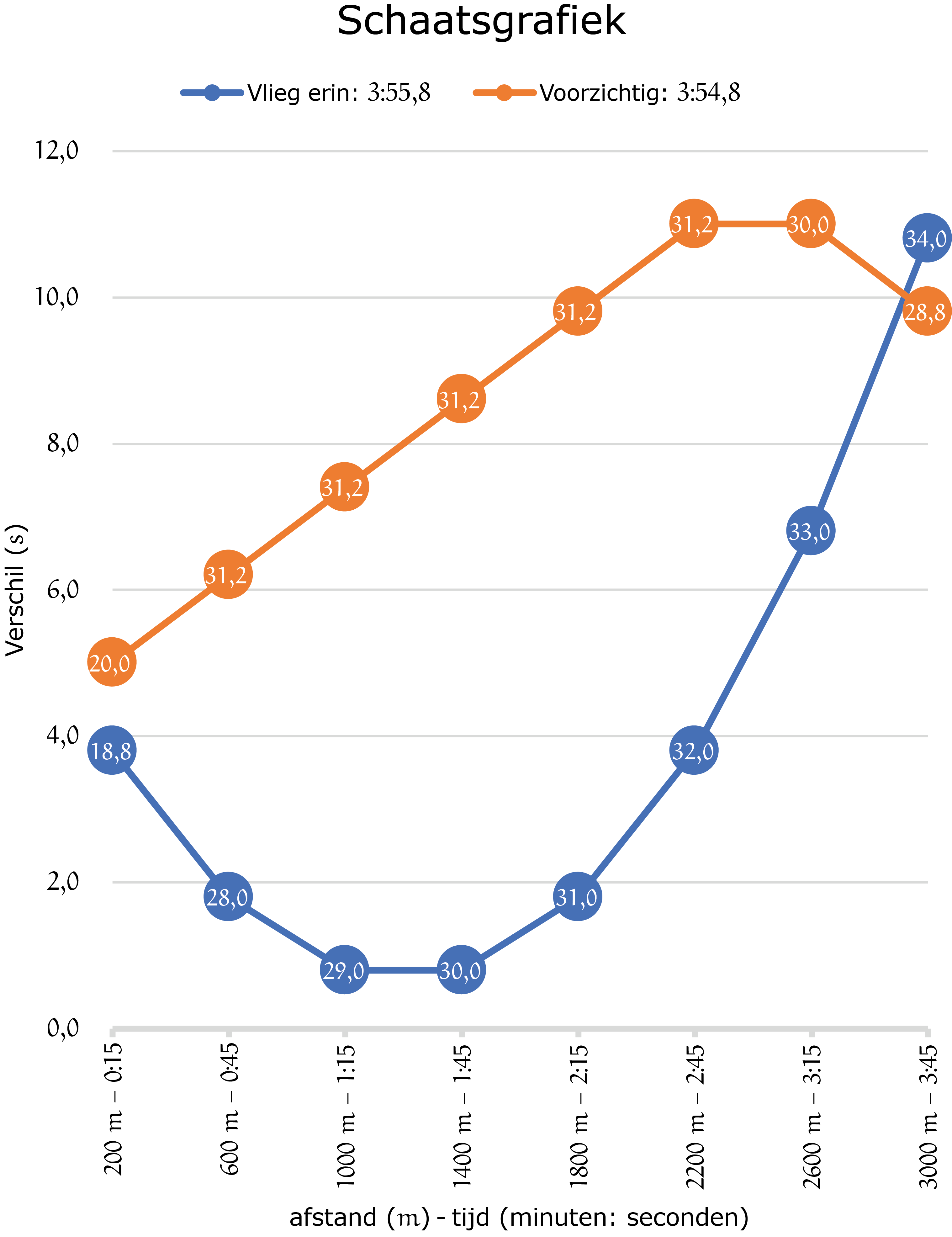
In deze schaatsgrafiek valt heel wat te zien. Kijk bijvoorbeeld eens op de blauwe lijn naar het bolletje met $30{,}0\ s$. Links ervan is de verbindingslijn horizontaal. Logisch, want we vergelijken met een toename van $30\ s$ per ronde. Kijk je naar de andere rondetijden, dan zie je dat de lijntjes links stijgen als ze groter dan $30\ s$ zijn en dalen als ze kleiner dan $30\ s$ zijn (zie bijv. de eerste rondetijden van 'vlieg erin'). Verder zijn ook alle tussentijden redelijk te schatten, dankzij de tijdinfo langs de horizontale as. 

Vraag

Kun je aan de hand van de schaatsgrafiek in figuur 4 nu de tussentijden van de schaatsers na $1800\ m$ schatten? Je kunt je schatting controleren met figuur 2 of narekenen met de tabel.

Tot slot

In dit artikel heb je gezien hoe je van schaatsdata een grafiek kan maken. Op dezelfde manier kun je ook grafiekjes maken van een zwemwedstrijd op basis van de tussentijden bij de keerpunten of een hardloopmarathon met kilometertijden. Je kunt op deze manier ook meerdere sporters vergelijken. Denk bijvoorbeeld aan de drie winnaars van een medaille van een wedstrijd.

Wereldrecord 5000 m Vorig jaar werd op 3 december het wereldrecord op de $5000\ m$ verbroken door de Zweed Nils van der Poel. Hij verbrak het vier jaar oude record van de Canadees Ted-Jan Bloemen. Beide records werden gereden op de hoog gelegen Amerikaanse ijsbaan van Salt Lake City. Daarvoor was het wereldrecord tien jaar in handen van Sven Kramer, gereden in Calgary (Canada). 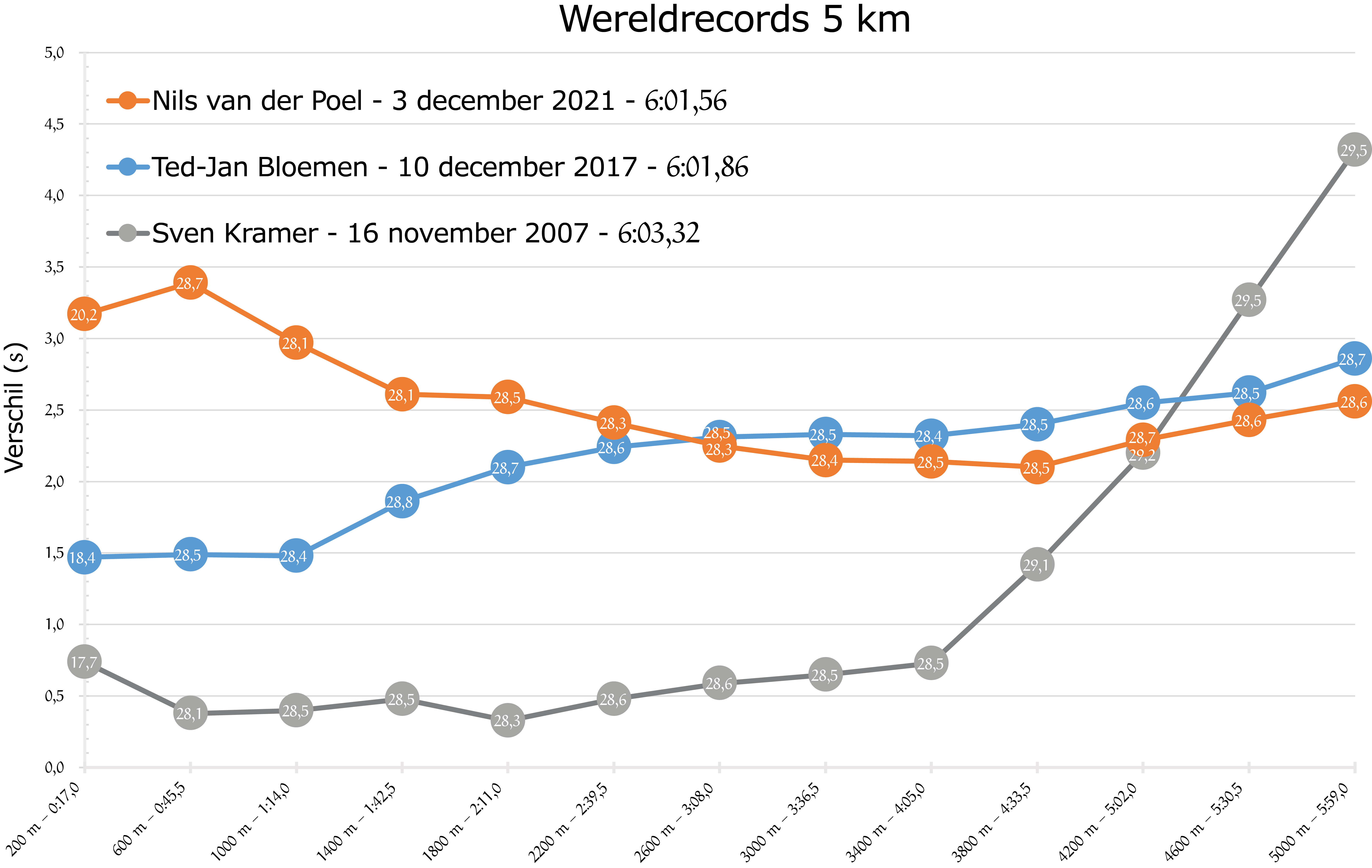De schaatsgrafiek in figuur 5 is precies zo gemaakt als in dit artikel beschreven. Er is nu vergeleken van met een toename van $28{,}5\ s$ per ronde. En van de eerste halve startronde is $17$ seconde afgehaald. Langs de horizontale as staat weer hoeveel er in totaal van de tussentijden is afgehaald. De bolletjes staan op de exacte hoogte van de tussentijd. In de bolletjes staan de afgeronde rondetijden. In de schaatsgrafiek zie je hoe vanaf $2600\ m$ Van der Poel met zijn tussentijden onder die van Ted-Jan Bloemen duikt. Het verschil tussen het oude en nieuwe wereldrecord blijft vanaf dat punt binnen een halve seconde. Sven Kramer ligt tijdens zijn recordrace in 2007 tot $3400\ m$ op koers voor een tijd onder de zes minuten, maar komt uiteindelijk ruim $3$ seconden boven de zes minuten uit.