In oude kerken kan heel wat wiskunde verstopt zijn. Soms wordt die wiskunde er met de haren bijgesleept. Thrillerauteurs als Dan Brown willen je doen geloven dat er mystieke symbolen in verwerkt zijn met diepe betekenissen die gewone mensen ontgaan. Die overdrijving ontneemt het zicht op wat er zich werkelijk afspeelde in de late middeleeuwen. Er is sprake van een fascinerende vooruitgang in ambacht, kennis en techniek. Vanaf de dertiende eeuw groeit het aantal mensen dat een uitgebreide kennis heeft van wiskunde, en dan vooral van de meetkunde van Euclides en de andere grootheden uit de Grieks-Romeinse tijd. De meesters van die tijd verdienen mijn oprechte bewondering. Na het tijdvak van de robuuste Romaanse architectuur wordt de Gotische bouwkunst verfijnder en levendiger. Architecten en hun opdrachtgevers zagen iedere keer nieuwe mogelijkheden om gedurfde ontwerpen ten uitvoer te brengen. Ook het vakmanschap van aannemers en steenhouwers ontwikkelde zich verder. Het boek Architect en aannemer, de opkomst van de bouwmarkt in de Nederlanden, 1350- 1530 schetst die ontwikkelingen nauwgezet, onderbouwd met vele voorbeelden op basis van gedetailleerd bronnenonderzoek. Kenmerk voor de Romaanse stijl is de driehoek, de vierhoek en de zeshoek. Pas in de latere gotiek verschenen vijfhoeken, zevenhoeken, tienhoeken of zelfs elfhoeken.

De kathedraal van Burgos in Noord-Spanje is een voorbeeld van rijk uitgevoerde gotiek met veel variatie in de vormentaal. In 2021 verscheen in Spanje een boek met de titel Teseros Matematicos de la Catedral de Burgos. Het is geschreven door wiskundigen en uitgegeven door de vereniging Miguel de Guzman, een actieve groep van wiskundedocenten. Het boek is zo goed geschreven dat ik zonder enige kennis van de Spaanse taal toch begrijp waar het over gaat. De foto’s en illustraties geven een goed beeld en bovendien zien wiskundige formules er in alle talen hetzelfde uit.

Internet staat vol met foto's en video's van deze kathedraal. Wanneer je de Nederlandse wikipedia pagina bezoekt, kijk dan ook eens op de Engelstalige of Spaanse pagina. Ook als je geen Spaans kent, is de trailer op de website cienciaycatedral.ubuinvestiga.es beslist de moeite waard.

In figuur 2 worden de onderdelen van de kathedraal benoemd. In deze bijdrage gaat het om de tienhoek rond de kooromgang en de apsis.

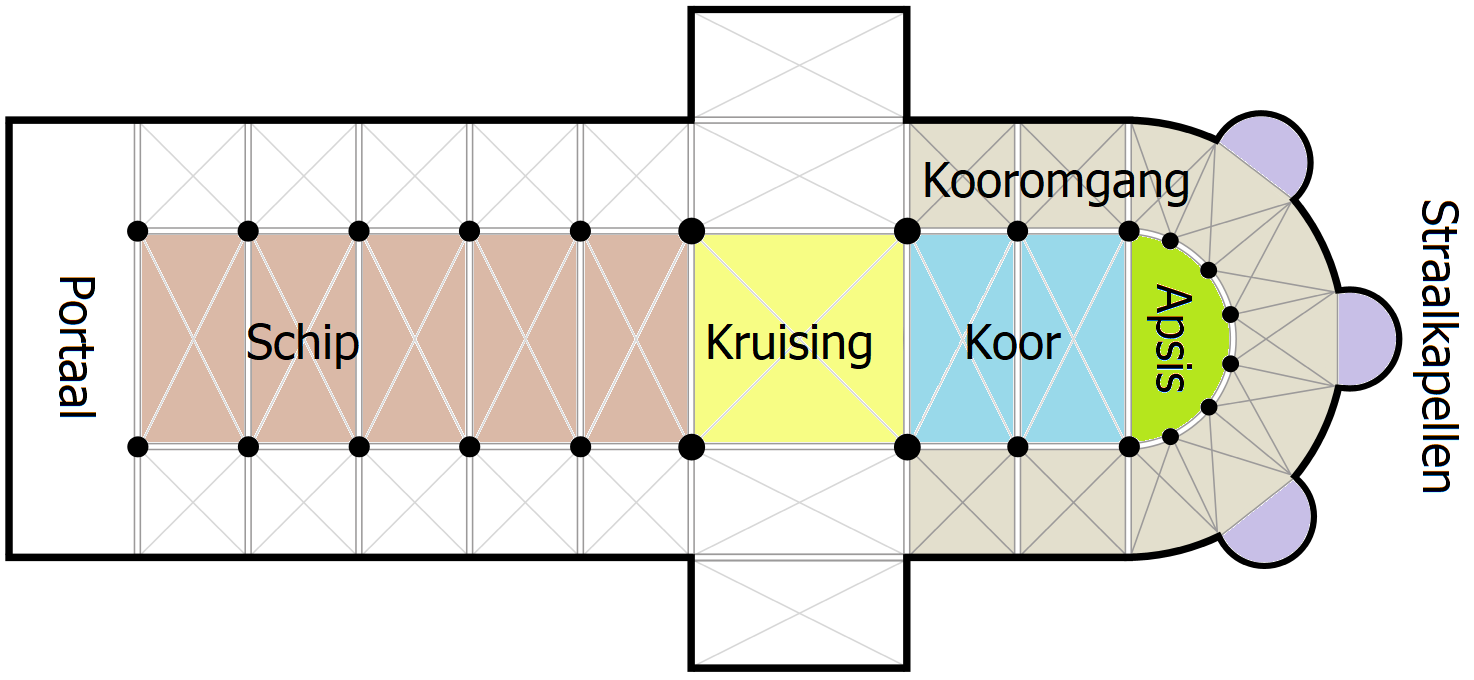
In figuur 3 zijn drie tienhoeken getekend. De eerste is om de apsis, de tweede om de kooromgang en de derde om de uiteinden van de straalkapellen. Binnen de tienhoeken zijn op de diagonalen tienpuntige sterren getekend. Het bijzondere van die tienpuntige ster is dat het één enkele zelfdoorsnijdende figuur is.

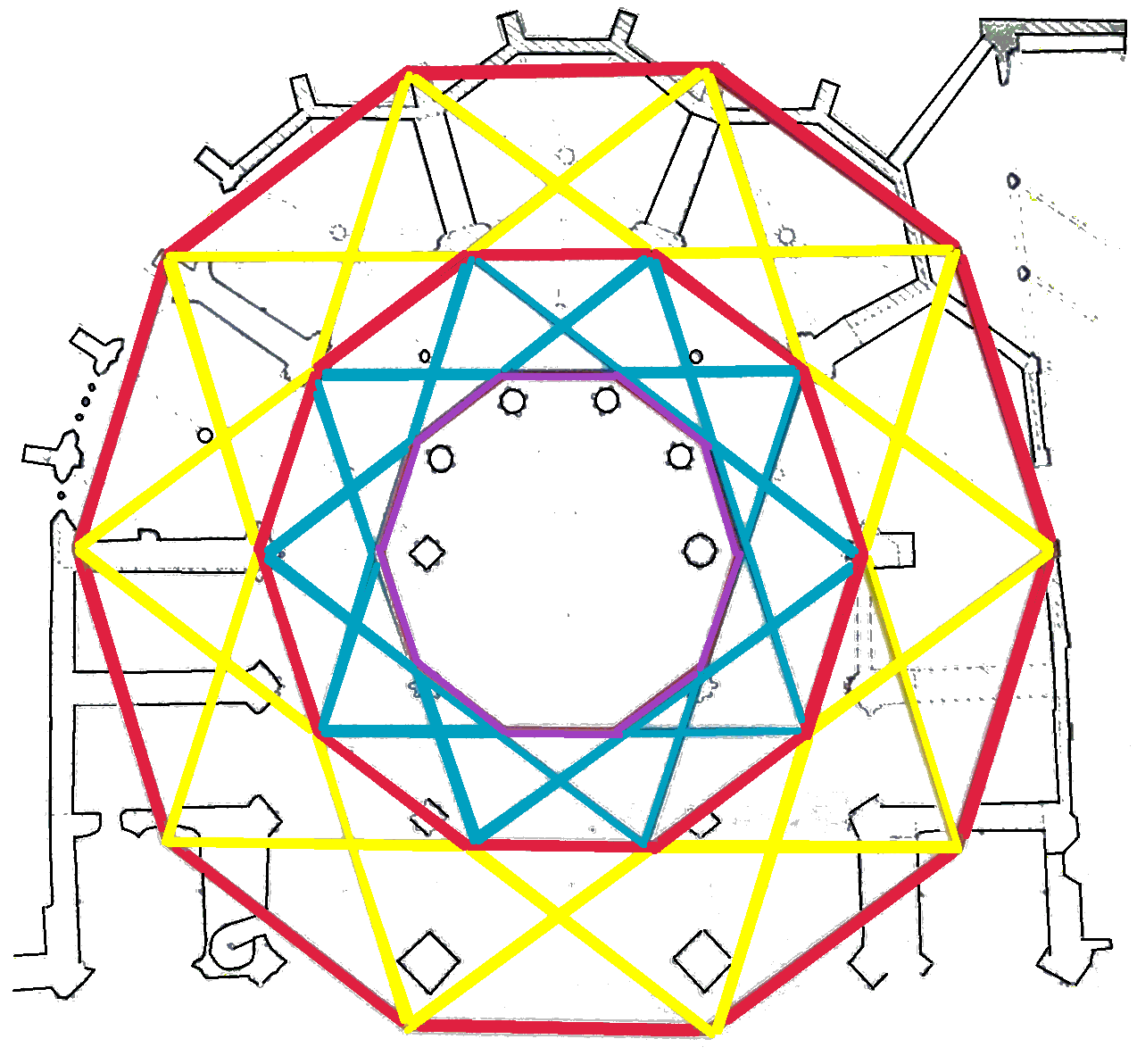
De tienhoeken zijn met elkaar verbonden door hun diagonalen. Iedere zijde van een binnenste tienhoek ligt op een diagonaal van de buitenste tienhoek, om precies te zijn, tussen het eerste en het vierde hoekpunt. Bijzonder is dat je met deze constructie zowel van buiten naar binnen kunt werken als van binnen naar buiten. Deze constructie gaat ons een meetkundige rij van lengtes van zijden bezorgen. Multatuli, bekend van de literatuurlijst Nederlands, noemt het geometrische progressie.

Lees op de website dbnl.org de brief van Multatuli aan Busken Huet, datum 15 augustus 1866, over gokken, kansrekening en de geometrische reeks.

 De verhouding tussen de lengte van de zijde van een buitenste tienhoek en een binnenste tienhoek is een speciale verhouding, het is namelijk de gulden snede verhouding. In de volgende opgaven ontdek je wat de gulden snede precies is, daarna ontdek je waar de gulden snede in een vijfhoek zit en tot slot bewijs je dat de constructie van opeenvolgende tienhoeken inderdaad opeenvolgende lengtes van zijden oplevert in de gulden snede verhouding.

De gulden snede kun je zien als het snijden van een lijnstuk in twee delen met een scherp mes.

Een lijnstuk met lengte $a + b$ is verdeeld in de gulden snede verhouding $\varphi$ wanneer het zodanig wordt verdeeld in een langste deel met lengte $a$ en een kortste deel met lengte $b$ dat

$$\frac{a+b}{a}=\frac{a}{b}$$

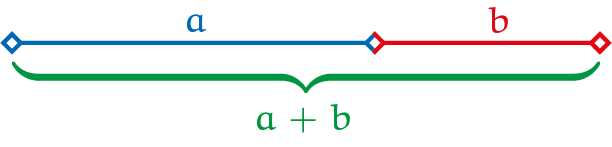
Opgave 1 Stel dat $b$ een getal is en dat die $a$ de onbekende is. Stel dat $b = 1$. Vul deze waarde van $b$ in de vergelijking $\frac{a+b}{a}=\frac{a}{b}$ in en toon aan dat $\frac{a}{b}=\frac{1+\sqrt{5}}{2}$. Dit getal noemen we $\varphi$.

Met algebra kun je aantonen dat dit waar is voor iedere waarde van $b$ door de vergelijking $\frac{a+b}{a}=\frac{a}{b}$ te herleiden tot $a^2 - ab - b^2 = 0$. Dit is een kwadratische vergelijking met onbekende $a$ met als oplossing $a=\frac{b\pm\sqrt{b^2+4b^2}}{2}$ zodat $\frac{a}{b}=\frac{1+\sqrt{5}}{2}$.

Uiteraard kun je deze uitdrukking ook zien als een kwadratische vergelijking met onbekende $b$, met dezelfde oplossing voor $\frac{a}{b}$. Omdat de verhouding tussen twee lengtes een positief getal is, kun je de oplossing met het minteken verwerpen omdat deze een negatief getal oplevert. Tot zover de algebra. Nu verder met meetkunde. In figuur 5 zie je regelmatige vijfhoek $ABCDE$ met middelpunt $M$ en zijde $AB = a$ en diagonaal $AD = a + b$. Met het laatste geven we alleen maar aan dat zijde $AD$ een stukje langer is dan zijde $AB$.

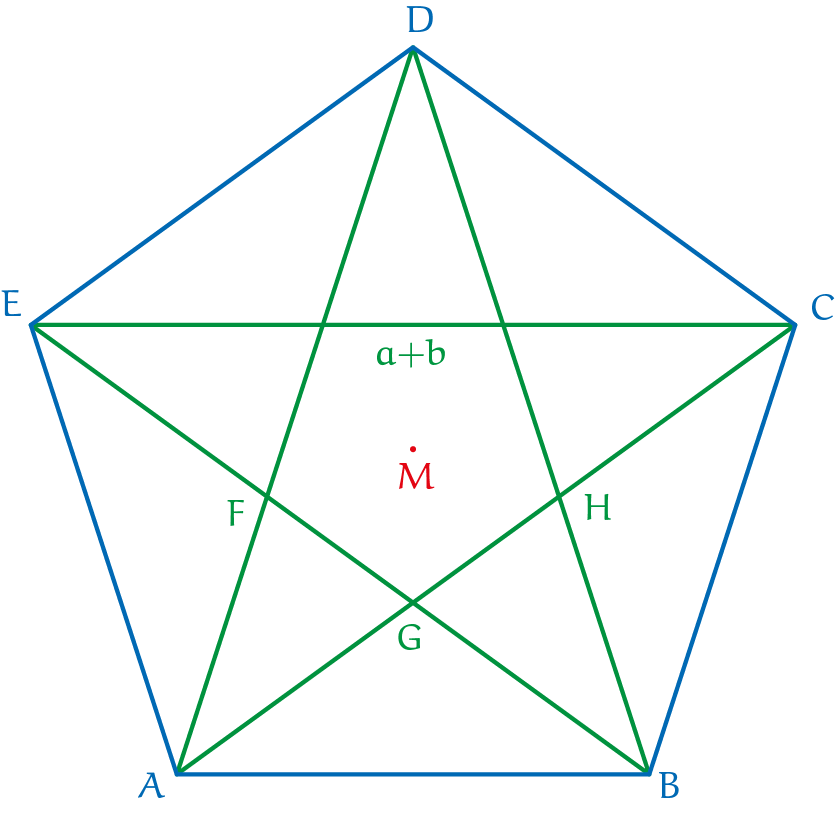
Opgave 2 Toon aan dat de grootte van alle hoeken van de driehoeken $AMB$, $ABC$, $ABF$, $ABG$ en $AFG$ veelvouden van $18^{\rm o}$ zijn. Opgave 3 Onderzoek welke driehoeken gelijkbenig zijn. Opgave 4 Onderzoek welke driehoeken een vergroting zijn van elkaar. Opgave 5 Toon aan dat de lengtes van de zijden van de driehoeken $ABC$ en $ABG$ zich verhouden in de gulden snede verhouding met $\frac{AC}{AB} = \frac{a+b}{a}=\frac{AB}{AG}=\frac{a}{b}$. Idem voor de driehoeken $ABD$, $ABF$ en $AFG$. Opgave 6 Toon aan dat in de gegeven vijfhoek $\frac{a}{b}=\varphi=\frac{1+\sqrt{5}}{2}$ de oplossing is van de vergelijking $\frac{a+b}{a}=\frac{a}{b}$. Opgave 7 Teken met Geogebra een regelmatige vijfhoek. Teken ook de diagonalen. Bepaal de lengte van de verschillende lijnstukken en stel vast dat de verhouding tussen de lengtes ongeveer gelijk is aan $$\frac{1+\sqrt{5}}{2}\approx 1{,}6.$$

Resultaat tot zover is dat je bewezen hebt dat in een gelijkbenige driehoek met tophoek $36^{\rm o}$ de lengtes van de benen zich verhouden tot de basis in de gulden snede verhouding. Evenzo verhoudt zich in een gelijkbenige driehoek met tophoek $108^{\rm o}$ de lengtes van de basis zich tot de lengte van de benen in de gulden snede verhouding. Deze driehoeken noemen we daarom gulden snede driehoeken.

Tot zover de vijfhoeken. Terug naar de tienhoek rond de apsis van Burgos. In figuur 6 zijn twee opeenvolgende tienhoeken getekend waarbij iedere zijde van de binnenste tienhoek ligt op een diagonaal van de buitenste tienhoek. Te bewijzen is dat de verhouding tussen de lengte van de zijde van de buitenste tienhoek en die van de binnenste tienhoek de gulden snede verhouding is.

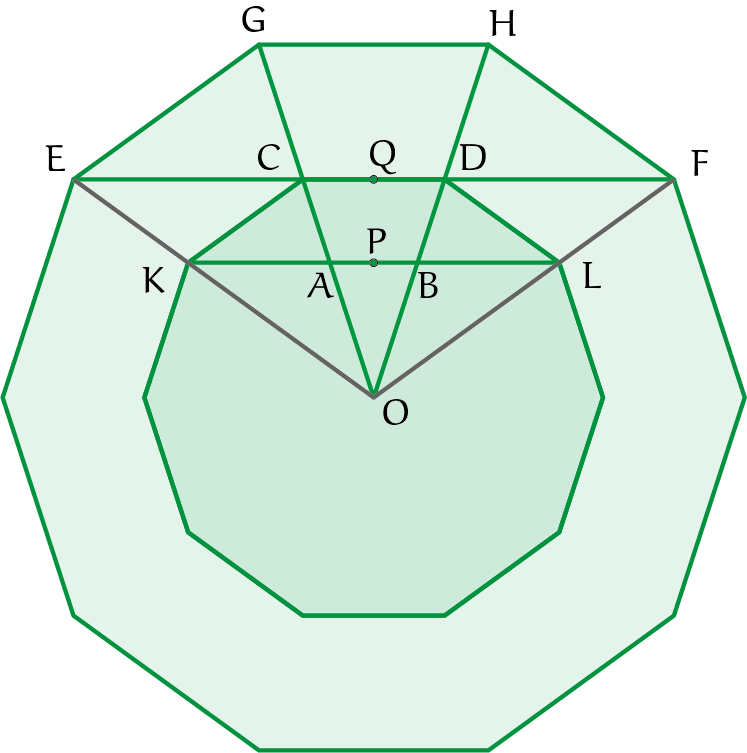
Opgave 8 Benoem in figuur 6 alle gulden snede driehoeken.

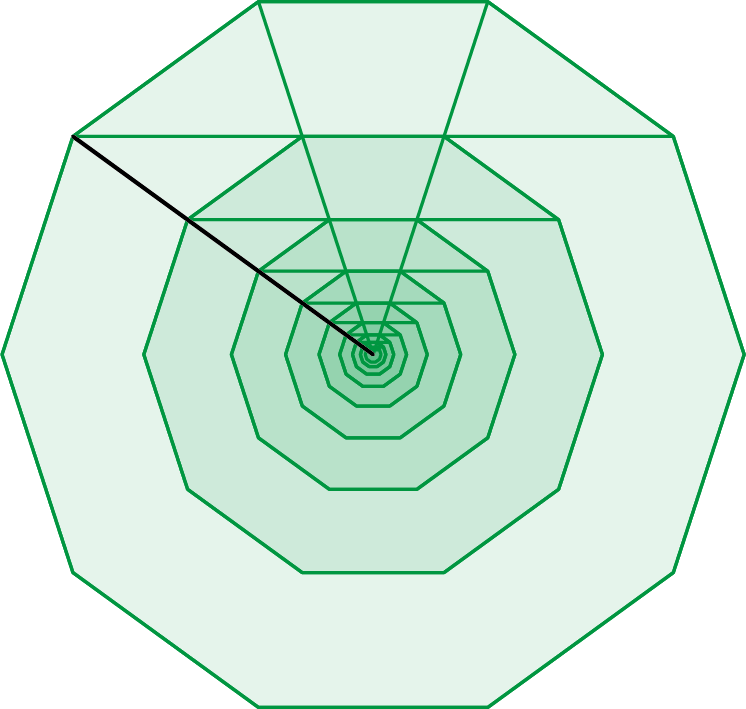
In figuur 7 zie je een opeenvolging van tienhoeken die alle op dezelfde manier geconstrueerd zijn. Geometrische progressie is zoals gezegd een oud begrip dat vandaag de dag niet meer genoemd wordt in de wiskundeboeken. Vandaag zeggen we "meetkundige rij". Een bijzondere meetkundige rij is die met de gulden snede $\varphi$ als reden (factor). 

Opgave 9 Bewijs dat de lengtes van de zijdes van opeenvolgende tienhoeken een meetkundige rij vormen met als reden de gulden snede verhouding.

Dit voorbeeld van de tienhoek rond de apsis is slechts één voorbeeld van de wiskunde in de kathedraal van Burgos. Andere voorbeelden betreffen vier cirkels in een vierkant, een achthoekig plafond en een gulden snede verhouding in een trapconstructie.

Constantino de la Fuente Martínez (2021), Teseros Matematicos de la Catedral de Burgos, Sociedad Castellano Leonesa De Educación Matematica Miguel De Guzmán, Burgos Merlijn Hurx (2012), Architect en aannemer, de opkomst van de bouwmarkt in de Nederlanden, 1350-1530, Nijmegen, Vantilt Nemo Kennislink: https://www.nemokennislink.nl/publicaties/het-geheim-van-de-gulden-snede/ Multatuli (1866), Brieven. Deel 7. Multatuli-Busken Huet 1866, brief van 15 augustus 1866 (DBNL: https://www.dbnl.org/tekst/mult001mdou09_01/mult001mdou09_01_0027.php) Multatuli (1872), Volledige werken. Deel 5. Millioenenstudiën. Divagatiën over zeker soort van liberalismus. Nog eens: vrye arbeid in Nederlands-Indië. Duizend-en-enige hoofdstukken over specialiteiten. Brief aan den Koning, Delft, Waltman (DBNL: https://www.dbnl.org/tekst/mult001gstu08_01/mult001gstu08_01_0013.php) La Ciencia que esconde la Catedral de Burgos (s.d.), https://cienciaycatedral.ubuinvestiga.es/ Asociación Castellana y Leonesa de Educación Matemática "Miguel de Guzmán" (s.d.),  https://www.socylem.es/sitio/ Animaties bij deze opdracht: https://www.geogebra.org/m/y4ck2x6e#material/epexrpbx

Bekijk oplossing