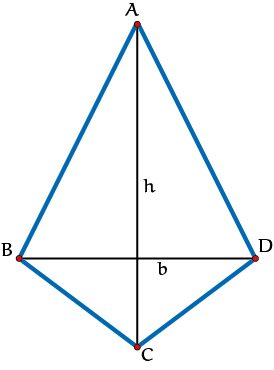
Het woord vlieger is ook de naam van een meetkundige vorm. De stokjes van de fysieke vlieger zijn de diagonalen van de meetkundige vlieger $ABCD$. In figuur 1 noem ik ze $b$ en $h$ voor breedte en hoogte. Als ik denk aan driedimensionale figuren, dan kijk ik bijvoorbeeld naar de platonische lichamen in figuur 2. Daar is de kubus een bekende vorm die opgebouwd is uit vierkante vliegers. Maar een vierkant voelt niet aan als een echte vlieger, hoewel hij voldoet aan de definitie. Als je gelijkmatig zou kunnen trekken aan de bovenste en onderste punten van de kubus zouden de 6 vierkanten kunnen veranderen in 6 ruiten en ruiten zijn ook vliegers (zie figuur 3). 

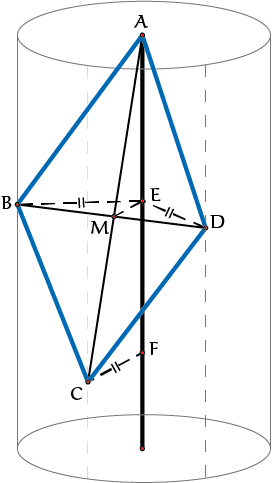
De kubus kan gezien worden als ruimtefiguur binnen een bol waarbij alle hoekpunten van de kubus op de bol liggen. Als je de kubus uitrekt, lukt dat niet meer. Je kunt dan een cilinder in gedachten houden als omheining waar de bovenste en onderste punten op de as van de cilinder liggen en de andere zes hoekpunten op de cilinder zelf. Denk aan een ruit $ABCD$ met middelpunt $M$. Als je deze ruit in de cilinder plaatst, zoals in figuur 4, met punt $A$ op de as van de cilinder dan liggen de punten $B$, $C$ en $D$ op de cilinder en dus op gelijke afstand van de as. Punt $M$ is dichter bij de cilinder-as. In de tekening zijn de afstanden van de cilinder-as voor de punten $M$, $D$ en $C$ met stippellijnen aangegeven.

 

Opgave 1 Hoe groot moet de hoek $MED$ zijn en wat zegt dat over de beperkte mogelijkheid om dit soort figuren met ruiten te bouwen?

 Het antwoord hierop valt tegen. Dan maar weer kijken naar de platonische lichamen. Daar zie ik de octaëder met acht zijvlakken.

Als ik aan de bovenste en onderste punten zou kunnen trekken krijg ik een figuur waar alle zijvlakken gelijkbenige driehoeken zijn. Hier zijn er vier driehoeken die elkaar ontmoeten in de bovenste en onderste punten. Dit zou mogelijk moeten zijn niet alleen voor het getal $4$ maar voor alle getallen $n \ge 3$. Zo’n figuur lijkt op een tol waar $n$ punten in een regelmatige $n$-hoek op de cilinder zitten en de onderste en bovenste punten op de cilinder-as. Ik noem de lengte van de zijden van de $n$-hoek $b$. Er is geen bovengrens voor de andere zijden van de driehoeken maar wel een ondergrens.

Opgave 2 Wat is die ondergrens in termen van $b$ en $n$?

Hier

hebben wij eigenlijk een ander antwoord op de kernvraag gekregen, want gelijkbenige driehoeken zijn ook enigszins vliegers: vliegers waar het kruispunt ligt op het eind van een van de stokjes. Dit is natuurlijk heel flauw en ik kan me voorstellen dat je zegt dat die vlieger niet opgaat. Het is toch een mooie plaats om te beginnen. Als de bovenste en onderste helften van de tol uit elkaar worden getrokken en gedraaid ten opzichte van elkaar is er ruimte om de driehoeken te vervangen met klassieke vliegers. En dan moeten alle nieuwe punten ook op de cilindermantel liggen. Zie figuur 5 waar $n = 4$.

Opgave 3 Maak weer gebruik van de cilinder en bepaal de verhouding $AM : AC$ in termen van $n$. Zie figuur 6.

Opgave 4 Als je een keuze hebt gemaakt voor $b$ (afstand $BD$) en $n$, hoe lang moet de andere vliegerdiagonaal (afstand $AC$) minimaal zijn?

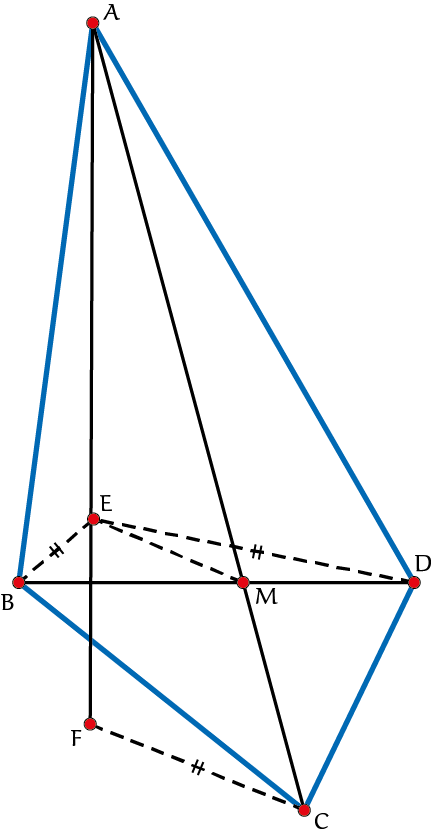
Opgave 5 Wat is nu de makkelijke formule voor de totale oppervlakte van zo’n figuur in termen van $b$ ($BD$), $h$ ($AC$) en $n$?

Als je een echt hoge vlieger wilt zien, kijk dan in Het vliegervierentwintigvlak in Pythagoras 42-5. Hier is de achterliggende basisfiguur niet een bol of cilinder maar een kubus.

 

 

Bekijk oplossing