Voor een eerste kennismaking met de cycloïde is het verstandig om het artikel 'De cycloïde: kromme van de kortste tijd' (Pythagoras 57-1, september 2017) te lezen.

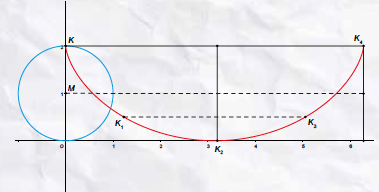
Als je een kraal in figuur 1 vanaf punt $K$ wrijvingsloos laat glijden langs een draad die de vorm van een cycloïde heeft, dan zal hij het onderste punt $K_2$ passeren en vervolgens verder gaan naar boven, tot hij weer stilstaat op het volgende hoogste punt, $K_4$. Dan zal hij opnieuw terugglijden en weer in $K$ aankomen, en zo zal hij steeds heen en weer gaan. De totale tijd om heen en weer te gaan noemen we de periode $T$.

Nu heeft de cycloïde, naast het feit dat het de brachistochroon is – kromme van de kortste tijd, zie het vorige artikel –, nog een prachtige eigenschap. Als we de kraal op een lager punt met snelheid 0 laten vertrekken (bijvoorbeeld in $K_1$), dan zal hij natuurlijk weer heen en weer gaan bewegen, met rechts van $K_2$ weer een nieuw hoogste punt $K_3$, even hoog als het startpunt. Ook deze periodieke beweging heeft een periode: $P$. We zullen aantonen dat, waar je de kraal ook uit stilstand laat vertrekken, altijd geldt: $P = T$. De periode is dus altijd dezelfde. Vandaar de Griekse benamingen tautochroon met ‘to auto’, ‘dezelfde’, of isochroon met ‘iso’, ‘gelijk’, en ‘chronos’, tijd. De periode van een hele slingering is dus onafhankelijk van de maximale uitwijking of amplitude. Om dit aan te tonen kijken we eerst even naar een andere isochrone beweging: een trillende massa aan een veer. Zie kader.

Een harmonisch trillende veer is isochroon

Een massa m hangt stil aan een veer. Bij uitrekking over $u$ is er een terugdrijvende kracht richting evenwichtsstand $F = −c \cdot u$, die recht evenredig is met u. Na uitrekken en loslaten gaat de massa een zogeheten harmonische trilling uitvoeren. De tweede wet van Newton zegt: $F = m \cdot u’’(t)$, waarbij $u’’(t)$ de versnelling is, de tweede afgeleide van $u(t)$ naar de tijd $t$. (De snelheid $v(t) = u’(t)$ is de eerste afgeleide van $u(t)$). Dus we hebben:

$$m\frac{d^2 u(t)}{dt^2}= −c · u(t)$$

Als je de afgeleide functie van de sinus- en de cosinusfunctie kent, zie je dat een oplossing van deze zogeheten differentiaalvergelijking de volgende is:

$$u(t) = A · \sin\left(\sqrt{\frac{c}{m}}t\right)$$

Opgave: Controleer dat de gegeven sinusfunctie voldoet aan de differentiaalvergelijking.

We vinden de periode $T$ door te stellen (de periode van de sinus is $2\pi$):

$\sqrt{\frac{c}{m}}T = 2\pi$ met $T = 2\pi \sqrt{\frac{m}{c}}$.

Maar belangrijker nog is dat de amplitude $A$ niet in de formule voor $T$ voorkomt. Die valt links en rechts na invullen in de differentiaalvergelijking weg. We kunnen voor $A$ dus nemen wat we willen. Dus een harmonische trilling is een isochrone trilling: de periode $T$ is onafhankelijk van de grootste uitwijking.

Kunnen we het resultaat uit het kader gebruiken om aan te tonen dat de glijdende kraal een isochrone beweging uitvoert? Dat kan. We noemen u de afstand langs de baan van de kraal tot het evenwichtspunt $K_2$.

We willen nu de grootte en richting bepalen van een klein stukje $\Delta u$ waarover de kraal langs de baan glijdt.

Zie daarvoor figuur 3 in het vorige artikel. Voor het gemak is een deel van die figuur hier als figuur 2 opgenomen.

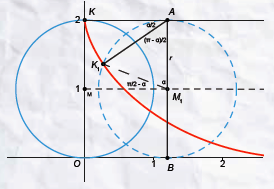
De hoek $\alpha$ is de ‘draaihoek’ $\alpha$ van het ‘wiel’ waarmee de cyclo.de wordt gemaakt ($MK$ gaat daarbij over in $M_1K_1$). Laten we nu $\alpha$ laten toenemen met een minuscuul hoekje $\Delta \alpha$. De buitenkant van het wiel draait dan over een stukje $r\Delta \alpha$. Zie figuur 3. Het middelpunt van het wiel gaat over hetzelfde stukje $r\Delta\alpha$ naar rechts (eigenschap van de cycloïde). Om $\Delta u$ te bepalen moeten we de twee stukjes $r\Delta\alpha$ als vectoren bij elkaar optellen. Dat levert $\Delta u=K_1T$.

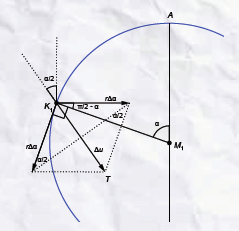
Opgave: Leid in de ruit in figuur 3 de volgende formule voor $\Delta u$ af :

$$\Delta u = 2r · \sin\left(\frac{1}{2}\alpha\right)$$

We zien dan ook direct dat de richting van de baan een hoek van $\alpha/2$ maakt met de verticaal.

Nu richten wij onze aandacht op de component van de zwaartekracht langs de baan. Zie figuur 4. Deze component drijft de kraal naar het ‘onderste punt’, de evenwichtsstand, net als bij de trillende veer. Hoe dichter de kraal bij $K_2$ is, des te kleiner is de kracht. Voor de component $F_r$ langs de raaklijn hebben we, zoals af te lezen in figuur 4:

$$F_r = mg · \cos\left(\frac{1}{2}\alpha\right)$$

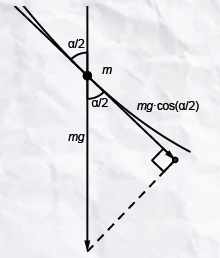
Bij de kleine verplaatsing $\Delta u$ langs de baan verandert $F_r$ een klein beetje $\Delta F_r$. De kracht aan het begin van $\Delta u$ noemen we $F_1$ en de kracht aan het eind $F_2$. We zetten deze twee vectoren in figuur 5 met samenvallende beginpunten neer om het verschil makkelijk te kunnen bepalen.

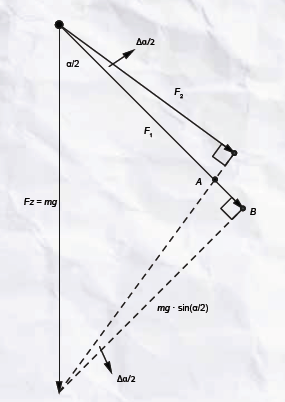
Opgave: Leid uit figuur 5 af dat voor $\Delta F_r = F_1 - F_2 = AB$ geldt:

$$\Delta F_r = mg · \sin\left(\frac{1}{2}\alpha\right)\frac{\Delta \alpha}{2}$$

Als we nu $\Delta \alpha$ elimineren uit de vergelijkingen voor $\Delta u$ en $\Delta F_r$, dan krijgen we:

$$\Delta F_r = \frac{mg}{4r}\Delta u$$

Omdat dit voor elk stukje van de baan geldt, geldt ook langs de hele baan:

$$F = \frac{mg}{4r}u$$

Omdat we alleen met lengtes en groottes gewerkt hebben, moeten we eigenlijk nu nog het minteken toevoegen. Dus geldt volgens het kader dat er langs de baan een harmonische trilling plaatsvindt, waarbij de periode $T$ onafhankelijk is van de maximale uitwijking. Dus de cycloïde is een isochroon.