
De driehoek van Sierpinski
Een bekende driehoek, waarvan de achtergrond anders en interessanter is dan je denkt
In het januarinummer van Pythagoras in 2021 staat een artikel over de kromme van Helge von Koch, een bijzondere vondst uit 1904: die kromme heeft in geen enkel punt een raaklijn.
In het aprilnummer van Pythagoras in 2022 staat ook een bijzondere kromme beschreven; deze werd in 1890 door Guiseppe Peano gemaakt. Die kromme vult het hele vierkant $\{(x,y):0 \le x,y \le 1\}$ in het vlak.
In 1915 beschreef de Poolse wiskundige Wacław Sierpiński een kromme die onderhand wereldberoemd is geworden als voorbeeld van een fractal; de kromme is overal te zien, ook in de sneeuw.
Dat van die fractal is een beetje een anachronisme. Het idee van 'fractal' is bijna half zo oud als de kromme en Sierpiński had een heel andere bedoeling met zijn constructie. De titel van het artikel is Sur une courbe dont tout point est un point de ramification. In vertaling: Over een kromme waarvan elk punt een vertakkingspunt is. Wat betekent dat en wat wilde Sierpiński ermee?
Wat is een kromme?
We hebben het er al eerder over gehad: wat is een kromme eigenlijk? De meeste mensen denken aan een beetje kronkelend lijntje dat je met een potlood op papier tekent; misschien met een lus er in en wat scherpe punten hier en daar, maar dan heb je het wel gehad.
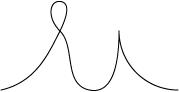
Zo'n punt waar een lus gevormd wordt heet wel een vertakkingspunt omdat daar meer dan twee lijnstukjes bij elkaar komen; in ons plaatje vier dus. Maar dat is een uitzonderlijkpunt lijkt het, in de andere punten komen altijd twee lijnstukjes samen.
Nu bleek het lastig te definiëren wat een kromme eigenlijk is en elke definitie had zo zijn uitzonderlijke gevallen. Een voor de hand liggende definitie is dat je de kromme door middel van bewegingsvergelijkingen moest kunnen beschrijven, dus als
$$\left\{\begin{matrix}
x=f(t) \\y=g(t)
\end{matrix}\right.$$
waarbij $f$ en $g$ functies zijn, gedefinieerd op het interval $[0, 1]$. Zo'n kromme wordt wel een Jordan-kromme genoemd.
De kromme van Peano is een Jordan-kromme; Peano had expliciet twee functies $f$ en $g$ gemaakt en laten zien dat ze bij gebruik in bewegingsvergelijkingen het hele vierkant doorlopen. In die kromme is elk punt vertakkingspunt: je kunt in elk punt zelfs oneindig veel intervallen samen laten komen.
Maar de kromme van Peano is natuurlijk erg dik: hij vult een heel vierkant. Daarom vond men ook dat krommen 'dun' moesten zijn: ze mochten niet een heel vierkantje opvullen. Zoiets noemde men een Cantor-kromme: binnen elk vierkantje in het vlak moet een kleiner vierkantje liggen waar de kromme niet doorheen gaat.
De Peano-kromme is dan een Jordan-kromme die geen Cantor-kromme is. In het septembernummer uit 2017 van Pythagoras staat de Poolse cirkel beschreven; dat is een Cantor-kromme die geen Jordan-kromme is. Het voorbeeld van Sierpiński laat zien dat zelfs als je beide definities samenneemt, je nog steeds iets kunt krijgen waarin elk punt een vertakkingspunt is.
Het voorbeeld
Die constructie van Sierpiński is welbekend maar we bekijken evengoed de oorspronkelijke beschrijving nog even om later de eigenschappen af te kunnen leiden. Ik heb de tekeningen uit het oorspronkelijke artikel gebruikt.
Sierpiński begon met een volle gelijkzijdige driehoek $T$ (van het Franse triangle, of het Poolse trójkąt) en verdeelde die, door de middens van de zijden te verbinden, in vier kleinere driehoeken $T_0$, $T_1$, $T_2$, en $U$.
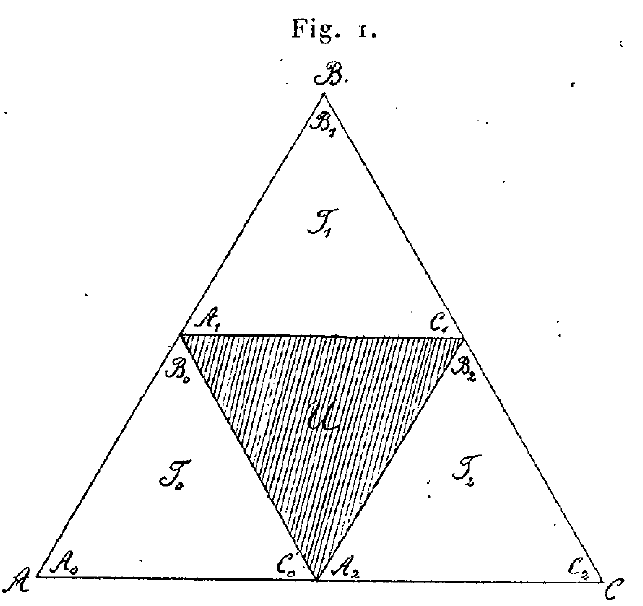
De binnenkant van driehoek $U$ liet hij weg; de volle driehoeken $T_0$, $T_1$, en $T_2$ blijven (tegenwoordig kleuren we de niet weggelaten driehoeken zwart, maar Sierpiński deed het net andersom). Hij herhaalde dit in elke overgebleven driehoek en als je goed kijkt zie je daar een codering van de overgebleven driehoeken verschijnen.
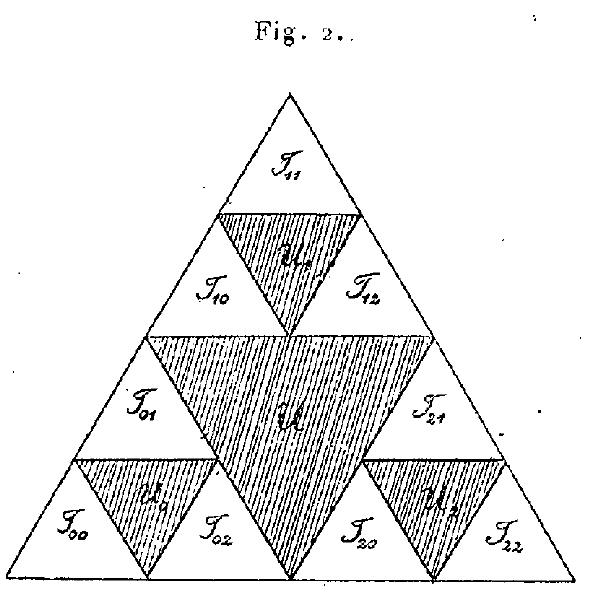
Het eerste cijfer in $T_{i,j}$ wijst de positie in de eerste verdeling aan: $0$ linksonder, $1$ boven, en $2$ rechtsonder. het tweede cijfer de relatieve positie bij de tweede verdeling: $T_{2,1} is de bovenste driehoek in de driehoek rechtsonder. Meer plaatjes van de constructie staan er niet in het artikel maar je kunt wel raden hoe het verder gaat.
Elk eindig rijtje $0$-en, $1$-en en $2$-en bepaalt een driehoek en als s zo'n rijtje is dan wordt de driehoek $T_s$ in vier driehoeken $T_{s,0}$, $T_{s,1}$, $T_{s,2}$ en $U_s$ verdeeld, waarna de binnenkant van $U_s$ wordt weggelaten.
Elke oneindige rij van $0$-en, $1$-en en $2$-en, zeg
$$\alpha_1, \alpha_2, \alpha_3, \dots$$
bepaalt een rijtje driehoeken
$$T_{\alpha_1} ,T_{\alpha_1,\alpha_2}, T_{\alpha_1, \alpha_2, \alpha_3}, \dots$$
waarvan de doorsnede precies één punt bevat. De driehoek van Sierpiński, die we $S$ noemen, bestaat uit alle punten die we zo verkrijgen.
Sommige punten van $S$ horen bij twee rijtjes $0$-en, $1$-en en $2$-en. Kijk bijvoorbeeld naar de rijtjes
$$0, 1, 1, 1, \dots \text{ en } 1, 0, 0, 0, \dots.$$
Het eerste rijtje geeft ons de top $B_0$ van $T_0$ en het tweede rijtje bepaalt het punt $A_1$ linksonder in $T_1$. Maar dat is twee keer hetzelfde punt: het midden van $AB$.
Met wat moeite kun je nagaan dat elk hoekpunt van een driehoek $T_s$ bij twee rijtjes hoort, behalve de hoekpunten van $T$ zelf, die horen bij de drie constante rijtjes.
Is S een kromme?
De verzameling $S$ is inderdaad een kromme, zowel in de zin van Cantor, als in de zin van Jordan.
Het eerste is het makkelijkst in te zien. Neem een vierkantje $V$ in het vlak en neem aan dat er een punt, $x$, van $S$ in $V$ zit (anders hoeven we niks te verifiëren). Bij $x$ hoort een rij driehoeken
$$T_{\alpha_1}, T_{\alpha_1, \alpha_2}, T_{\alpha_1, \alpha_2, \alpha_3}, \dots$$
waarvan de doorsnede uit precies het punt $x$ bestaat. De lengte van de zijde van elke volgende driehoek is telkens de helft van die van de voorafgaande. Er is dus een driehoek $T_s$ die helemaal binnen $V$ ligt (wacht tot de zijden korter zijn dan de afstand van $x$ tot de rand van $V$). Dan ligt de weggelaten driehoek $U_s$ binnen $V$ maar buiten $S$; neem dus een klein vierkantje binnen $U_s$ om aan de definitie te voldoen.
Om in te zien dat het een Jordan-kromme is gaan we net zo te werk als bij de Peanokromme. We plannen een reis door $S$ door onze plannen steeds te verfijnen. We moeten dus voor elk tijdstip $t$ in $[0, 1]$ aangeven waar we dan zullen zijn. De plaatjes komen weer uit het artikel van Sierpiński.
Kijk nog even goed naar het eerste plaatje van Sierpiński. Daar zie je dat voor $T_i$ de drie hoekpunten telkens $A_i$, $B_i$, en $C_i$ genoemd worden (met $i = 0, 1, 2$). Het is in zijn tweede plaatje niet te zien maar in het artikel wel: de hoekpunten van $T_{i,j}$ zijn $A_{i,j}$, $B_{i,j}$ en $C_{i,j}$. En dit gebeurt overal: het label van een driehoek $T_s$ hangen we ook aan de hoekpunten: $A_s$, $B_s$ en $C_s$; en altijd in dezelfde volgorde. We hebben ook al gezien dat bijna alle hoekpunten twee namen krijgen. We willen beginnen in $A$ en eindigen in $C$ en dat gaat zo

Op tijstip $0$ zijn we in $A$ en op tijdstip $1$ willen we in $C$ zijn.
We passen de reis wat aan om meer van de verzameling $S$ te zien, we verleggen onze route via $B_0$ en $B_2$:
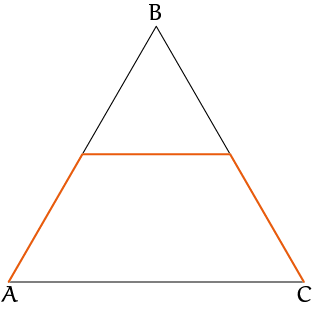
We plannen ons reisschema zó dat we op tijdstippen $1/3$ en $2/3$ in respectievelijk $B_0$ en $B_2$ zijn.
Vervolgens breiden we het reisplan uit door wat omwegen in de intervallen $[0, 1/3]$, $[1/3, 2/3]$ en $[2/3, 1]$ te maken. Zo gaat de reis van $A$ naar $B_0$ via $C_{0,0}$ (als $t = 1/9$) en $C_{0,1}$ (op tijdstip $2/9$). Van $B_0$ naar $B_2$ gaat via $B_{1,0}$ en $B_{1,2}$; en van $B_2$ naar $C$ doen we via $A_{2,1}$ en $A_{2,2}$.

Elk van de negen lijnstukjes is zijde van één van de negen overgebleven driehoeken $T_{i,j}$; in elk van die driehoeken verleggen we de reisroute zó dat we van elk van $T_{i,j,0},$ $T_{i,j,1}$, en $T_{i,j,2}$ een zijde meenemen (niet altijd in die volgorde). We krijgen dan deze route:
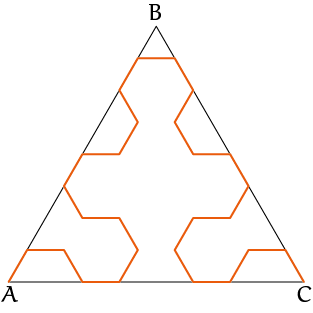
Dat aanpassen van het reisschema gaat zo maar door, en telkens op dezelfde manier. Een paar stappen verder begin de reisroute al aardig op de driehoek van Sierpiński te lijken, hier is nummer zeven:

Voor elk van de routes die we getekend hebben kun je bewegingsvergelijkingen opstellen. Dat is wat gepuzzel maar het kan. Je krijgt dan twee rijen functies
$$f_1, f_2, f_3, \dots \text{ en } g_1, g_2, g_3, \dots$$
en die rijen convergeren naar twee continue functies $f$ en $g$. De bewegingsvergelijkingen die bij $f$ en $g$ horen beschrijven precies de verzameling $S$.
Vertakkingspunten
Nu moeten we nog nagaan dat elk punt een vertakkingspunt is. Dat is niet helemaal waar: de hoekpunten $A$, $B$ en $C$ zijn geen vertakkingspunten, maar daar had Sierpiński nog een oplossing voor, en die komt zo. We kijken eerst naar de andere punten.
Als $x$ een middelpunt van een zijde van een driehoek $T_s$ is, dan is makkelijk in te zien dat het een vertakkingspunt is. Kijk bijvoorbeeld naar het punt dat in de originele figuur 1 van Sierpiński de namen $B_0$ en $A_1$ heeft: daar komen twee zijden van $T_0$ en twee zijden van $T_1$ samen.
Als $x$ niet een hoekpunt van een driehoek $T_s$ is, dan moeten we beter kijken. Bij $x$ hoort een oneindige rij $0$-en, $1$-en en $2$-en,
$$\alpha_1, \alpha_2, \alpha_3, \dots$$
en dus een rij driehoeken
$$T_{s_1}, T_{s_2}, T_{s_3}, \dots$$
waarbij $s_n = \langle a_1, \dots ,a_n\rangle$ (het beginstuk van lengte $n$).
Stel dat de rij begint met $0, 1, 2, 0, 1, 2, \dots$. Dan begint de rij driehoeken met
$$T_{\langle 0\rangle}, T_{\langle 0,1\rangle}, T_{\langle 0,1,2\rangle}, T_{\langle 0,1,2,0\rangle}, T_{\langle 0,1,2,0,1\rangle}, T_{\langle 0,1,2,0,1,2\rangle}, \dots.$$
Die driehoeken zijn in hieronder ingetekend:
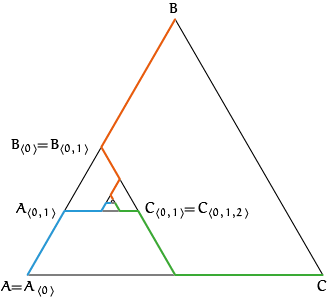
In de tekening zijn de overeenkomstige hoekpunten van de driehoeken op volgorde met lijnstukjes verbonden; in het blauw: $A$, $A_{\langle 0\rangle}$, $A_{\langle 0,1\rangle}$, $A_{\langle 0,1,2\rangle}$, $A_{\langle 0,1,2,0\rangle}$, $A_{\langle 0,1,2,0,1\rangle}$ en $A_{\langle 0,1,2,0,1,2\rangle}$. De oranje lijnstukjes verbinden de $B$'s en de groene de $C$'s. Opletten: de volgende driehoek heeft altijd een hoekpunt gemeen met de huidige. Bijvoorbeeld $A = A_{\langle 0\rangle}$, $B_{\langle 0\rangle} = B_{\langle 0,1\rangle}$, $C_{\langle 0,1\rangle} = C_{\langle 0,1,2\rangle}$, enzovoort.
Als je de de hele rij $0$-en, $1$-en en $2$-en die bij $x$ hoort zo afloopt krijg je drie krommen die uit rechte lijnstukjes bestaan, die elkaar nooit snijden, en die in $x$ samenkomen. Dat laat zien dat $x$ een vertakkingspunt is.
En de drie hoekpunten?
Nu weten we nog niet dat de drie hoekpunten $A$, $B$, en $C$ vertakkingspunten zijn. In plaats van te onderzoeken of het ook vertakkingspunten zijn deed Sierpiński iets anders: hij nam zes kopieën van de driehoek en legde die tot een mooie zeshoek:

Het resultaat is nog steeds een Cantor en Jordan-kromme: als je de $B$-en in het midden legt dan kun je onze bewegingsvergelijkingen herhalen en zo tegen de klok in de hele kromme doorlopen. De $B$-en in het midden vormen nu ook een vertakkingspunt, en omdat de $A$-en en $C$-en aan elkaar geplakt worden zijn de zes hoekpunten nu ook vertakkingspunten: er komen telkens drie lijnstukken samen.
| Er is veel meer te vertellen over de driehoek van Sierpiński. De Engelse wikipediapagina "Sierpiński triangle" staat vol informatie en verwijzingen naar artikelen en boeken waar je meer kunt leren. |
||||
|
Je kunt de oorspronkelijke artikelen van Sierpiński ook online lezen. Er is een korte versie in het Frans: |
||||
