Als je in de Van Dale het woord ‘lemniscaat’ opzoekt, vind je

1. wiskunde: de voetpuntskromme van een gelijkzijdige hyperbool t.o.v. het middelpunt, en tevens de inversie daarvan t.o.v. hetzelfde punt = striklijn (1)

Als je naar ‘striklijn’ gaat, vind je als eerste betekenis

1. wiskunde: lijn die een strik vertoont, t.w. de vorm heeft van een 8 = lemniscaat (1)

Dat is mooi: een lemniscaat is een striklijn en een striklijn is een lemniscaat. Maar als je de twee definities naast elkaar legt, dan zeggen die niet hetzelfde: een lemniscaat is een heel specifieke kromme en een striklijn hoeft alleen maar de vorm van een 8 te hebben.

We bekijken eerst de kromme die aan de definitie van ‘lemniscaat’ voldoet. Daarna nemen we wat andere striklijnen onder de loep.

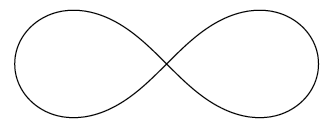
Lemniscaat van Bernoulli

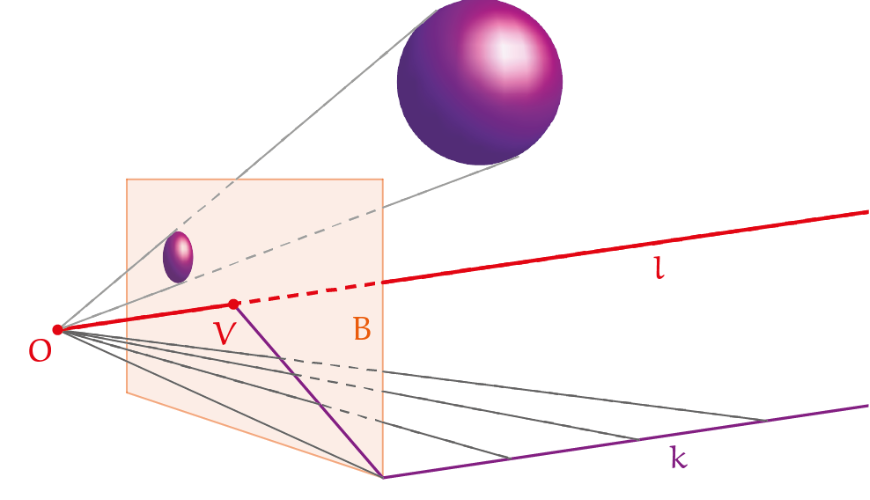
Bij de definitie van ‘lemniscaat’ staat, in de online versie van Van Dale, een plaatje. Dat plaatje (zie figuur 1) hoort inderdaad bij de definitie die gegeven is. Een gelijkzijdige hyperbool is er een waarvan de lijnen y = ±x de asymptoten zijn; zo’n hyperbool heeft een vergelijking van de vorm $x^2 – y^2 = c$. Wij nemen c = 1. Het middelpunt van de hyperbool is dan gewoon de oorsprong.

De voetpuntskromme ten opzichte van een punt krijg je door alle raaklijnen aan de hyperbool te trekken en daar telkens dat punt loodrecht op te projecteren.

Neem nu $P = (x_0, y_0)$ op de hyperbool (zie figuur 2). We berekenen de loodrechte projectie van de oorsprong op de raaklijn in P aan de hyperbool. Die raaklijn heeft de vergelijking $x_0x – y_0y = 1$ en de lijn door de oorsprong die daar loodrecht op staat heeft vergelijking $y_0x + x_0y = 0$. Het snijpunt, P’, is gelijk aan $(x_0/(x_0^2 + y_0^2), –y_0/(x_0^2 + y_0^2)).$

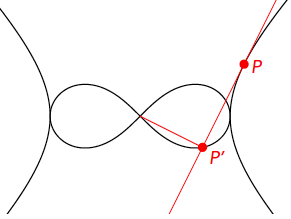
Opgave 1. Reken na dat $x_0x – y_0y = 1$ inderdaad de raaklijn in P geeft: het punt $(x_0, y_0)$ is het enige punt dat op de lijn en op de hyperbool ligt. 

Nu kun je een vergelijking van de lemniscaat opstellen: schrijf

$u = x_0/(x_0^2 + y_0^2)$ en $v = –y_0/( x_0^2 + y_0^2).$

Dan geldt

$$u^2 + v^2 = 1/(x_0^2 + y_0^2)$$ en $$u^2 – v^2 = 1/( x_0^2 + y_0^2)^2$$ (reken maar na) en dus $$u^2 – v^2 = (u^2 + v^2)^2.$$

Opgave 2. Reken na dat als je met de hyperbool met vergelijking $x^2 – y^2 = c^2$ begint, je de volgende vergelijking voor de lemniscaat krijgt: $(u^2 + v^2)^2 = c^2(u^2 – v^2)$. 

Opgave 3. De definitie van de lemniscaat gaat uit van het middelpunt, maar je kunt natuurlijk ook voetpuntskrommen voor andere punten maken. Maak die krommen met behulp van GeoGebra voor verschillende punten in het vlak. Je kunt zien dat er geen strik ontstaat zodra je een punt in een van de twee buitengebieden van de hyperbool neemt. Je krijgt wel een strik bij punten in het middengebied.

Lemniscaat van Booth

De definitie van ‘striklijn’ zou je heel ruim kunnen opvatten: alles wat maar een beetje op een 8 lijkt mogen we ‘striklijn’, en dus ‘lemniscaat’, noemen. We hebben zojuist de lemniscaat van Bernoulli gezien. Dat is een speciaal geval van de lemniscaat van Booth.

Deze krijg je als je een torus – dat is jargon voor iets dat de vorm van een fietsband of een donut heeft – met een vlak snijdt: meestal krijg je twee krommen die op cirkels lijken of een ovaal (soms met deukjes er in), maar als het vlak precies de binnenste cirkel van de torus raakt, krijg je iets wat ook op een 8 lijkt.

Een liggende torus kun je beschrijven met de volgende vergelijking: $$(\sqrt{x^2 + y^2} −b)^2 +z^2 =a^2 $$. Hierbij is b de straal van de hartcirkel van de torus en a de straal van de torusbuis zelf. Als je de torus snijdt met een vlak met vergelijking x = c, krijg je de twee cirkelachtige krommen als |c| < b – a en één ovaal-achtige kromme als b – a < |c| < b + a. Maar als |c| = b – a, dan komt er een figuur die op een 8 lijkt. Met wat doorzettingsvermogen kun je de volgende vergelijking afleiden: $$(y^2 + z^2)^2 = 4bay^2 – 4b(b – a)z^2.$$ Die lijkt wel op de vergelijking van de lemniscaat van Bernoulli: als b = 2a, dan staat er $$(y^2 + z^2)^2 = 8a^2(y^2 – z^2)$$ en dat is precies de vergelijking uit opgave 2, met c = 2a√2.

De vorm van de lemniscaat hangt af van de verhouding b/a; als je de straal a (de halve dikte van de buis) constant houdt, dan blijft de hoogte van de lemniscaat ook vast: 2a. Als je b laat groeien, wordt de lemniscaat steeds uitgerekter.

De lemniscaten van Booth werden al door de oude Grieken bestudeerd en hippopede genoemd. Een hippopede heet in het Nederlands een kluister; dat is eigenlijk een stel handboeien voor paarden;die werden wel gebruikt om de benen van paarden bij transport vast te zetten.

Opgave 4. Een ‘willekeurige’ hyperbool heeft een vergelijking van de vorm $$\frac{x^2}{ a^2} − \frac{y^2}{ b^2} =1.$$ Maak hiervan de voetpuntskromme ten opzichte van de oorsprong en ga na dat je zo ook de lemniscaten van Booth krijgt.

Lemniscaat van Gerono

Een andere lemniscaat is die van Gerono. Je maakt hem als volgt. Neem de cilinder met vergelijking $y^2 + z^2 – z = 0$. Die ligt op de x-as en heeft straal $\frac{1}{ 2}$. Deze cilinder snijden we met de bol $x^2 + y^2 + z^2 = 1$. Als je eerst $z^2 – z + y^2 = 0$ met behulp van de abc-formule oplost naar z en het resultaat invult in de vergelijking van de bol, dan krijg je na enig rekenwerk de vergelijking van de projectie van de snijkrommen in het xy-vlak: $$x^4 – x^2 + y^2 = 0$$ (zie figuur 3). Als je deze lemniscaat zelf wilt tekenen, dan is dat niet zo lastig: er geldt $$y =± \sqrt{x^2 −x^4} =±x\sqrt{1−x^2}$$ en je hoeft alleen de grafiek van die functie te schetsen (of te plotten).

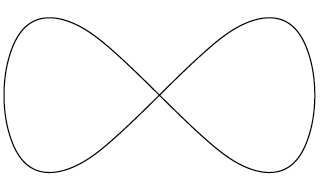
Krommen van Watt

Een hele familie van krommen die veel of een beetje op een 8 lijken kun je maken met een constructie die bedacht is door James Watt, de uitvinder van de stoommachine. Omdat Watt draaiende bewegingen in rechte bewegingen moest omzetten (en omgekeerd), experimenteerde hij met allerlei stangen die tussen en langs cirkels bewogen.

In het algemeen gaat de beschrijving als volgt: neem twee cirkels met straal b en met hun middelpunten in (–a, 0) en (a, 0). Daarnaast neem je een lijnstuk van lengte 2c en zet de uiteinden op de cirkels. Laat het lijnstuk nu bewegen en volg de baan van het middelpunt. We bekijken natuurlijk alleen situaties waarin deze methode iets oplevert.

Een mooi voorbeeld krijg je met a = 1, b = √2 en c = 1 (zie figuur 4). Dan kan het lijnstuk op twee manieren bewegen. Je kunt het horizontaal houden, dan beschrijft het middelpunt de cirkel met straal b om (0, 0) (blauw). Maar je kunt het lijnstuk ook horizontaal laten beginnen met de uiteinden in (–1 + √2, 0) en (1 + √2, 0) en dan het linkeruiteinde omlaag laten gaan en het rechteruiteinde omhoog (rood).

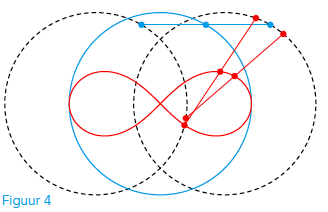
De figuur die je dan krijgt, is het logo van de Internationale Wiskunde Olympiade: een cirkel met daarin een lemniscaat van Bernoulli.

Opgave 5. Maak een animatie van dit proces in GeoGebra en varieer de waarden van a, b en c om te kijken wat voor 8-achtige figuren je zo nog meer kunt maken.

Overigens geeft de Van Dale voor ‘lemniscaat’ ook nog een andere betekenis:

2. symbool van het evenwicht tussen het stoffelijke en het geestelijke.

Dat lijkt ons erg geschikt voor een ander type tijdschrift...