Projectieve meetkunde komt voort uit het perspectieftekenen. Tekeningen in perspectief en foto’s beelden de werkelijkheid af zoals we die met onze eigen ogen zien. Daarbij gelden drie regels, die we zullen uitleggen:

1. rechte lijnen worden afgebeeld op rechte lijnen,
2. beelden van parallelle lijnen zijn parallel of hebben een gemeenschappelijk verdwijnpunt,
3. beelden van parallellen aan lijnen in een bepaald vlak komen samen op een gemeenschappelijke lijn, de verdwijnlijn van dat vlak, die ook de verdwijnlijn is van alle andere vlakken parallel aan dat vlak.

Verdwijnpunten zijn noodzakelijk voor perspectieftekenen en handig voor het gebruik van de dubbelverhouding, het onderwerp van dit artikel. We beginnen daarom met het concept verdwijnpunt.

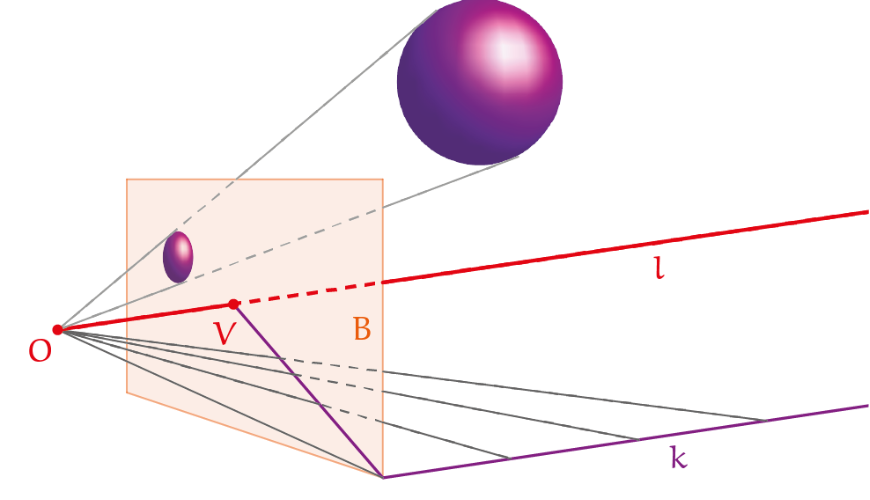
Figuur 4 verderop is een foto van een straatbeeld waarin de genoemde regels hierboven te herkennen zijn. We onderzoeken hoe dit meetkundig in elkaar zit door te kijken hoe lijnen uit de ruimte worden afgebeeld op een plat vlak. Figuur 1 toont hoe de projectie met centrum $O$ de $\color{purple}{paarse}$ bol en halfoneindige rechte lijn $k$ afbeeldt op het beeldvlak $B$. Hoe de bol wordt geprojecteerd is gemakkelijk te zien. Laten we kijken naar lijn $k$. Ieder punt op de $\color{purple}{paarse}$ lijn wordt met behulp van een $\color{grey}{grijze}$ projectiestraal afgebeeld op een punt in het beeldvlak. Zo wordt de rechte lijn afgebeeld op een rechte lijn (regel 1). De denkbeeldige $\color{red}{rode}$ lijn $l$ is de lijn vanuit het gezichtspunt $O$ (het oog, de camera) parallel aan de gegeven paarse lijn. Hoe verder een punt op de $\color{purple}{paarse}$ lijn van het beeldvlak verwijderd is, des te dichter ligt het bijbehorende beeldpunt bij het punt $V$ waar de $\color{red}{rode}$ lijn het beeldvlak doorboort, en des te kleiner is de hoek tussen de $\color{grey}{grijze}$ projectiestraal en de $\color{red}{rode}$ lijn. Het punt $V$ heet het verdwijnpunt van $k$ en de $\color{red}{rode}$ lijn heet de verdwijnstraal. 

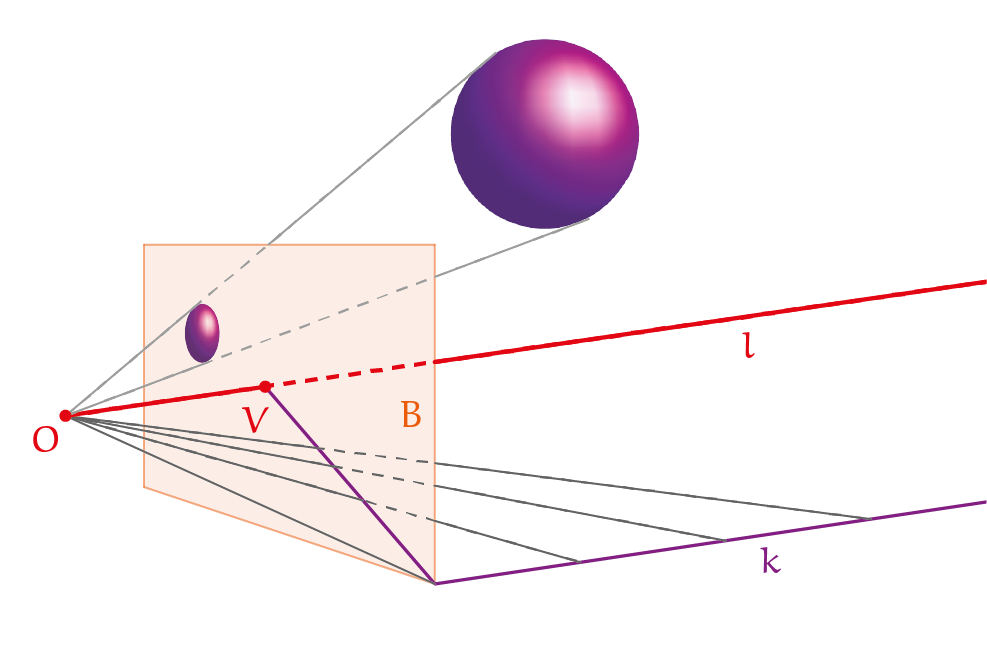
De richting van de $\color{purple}{paarse}$ lijn is willekeurig gekozen (maar niet parallel aan het beeldvlak). Alle andere lijnen parallel eraan hebben dezelfde verdwijnstraal en hetzelfde verdwijnpunt. Zo heeft elke richting zijn eigen verdwijnpunt, dat herkenbaar is zodra er op het beeldvlak lijnen zichtbaar zijn die ernaartoe lopen. In figuur 3 herken je de aanwezigheid van een verdwijnpunt voor de verticale richting, hoewel het buiten de foto valt.

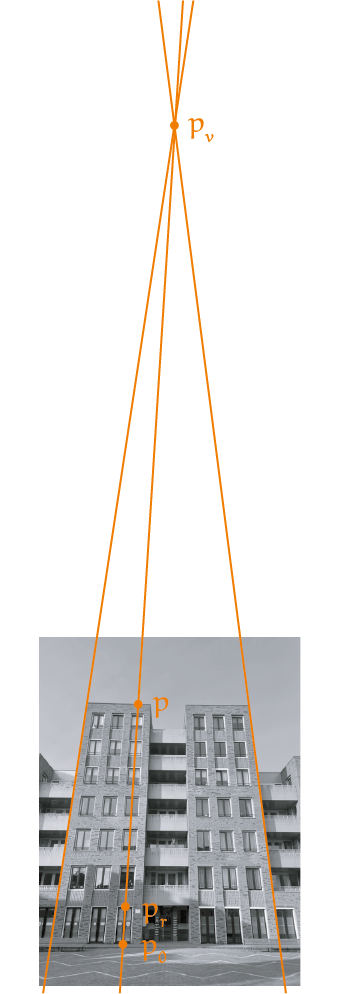
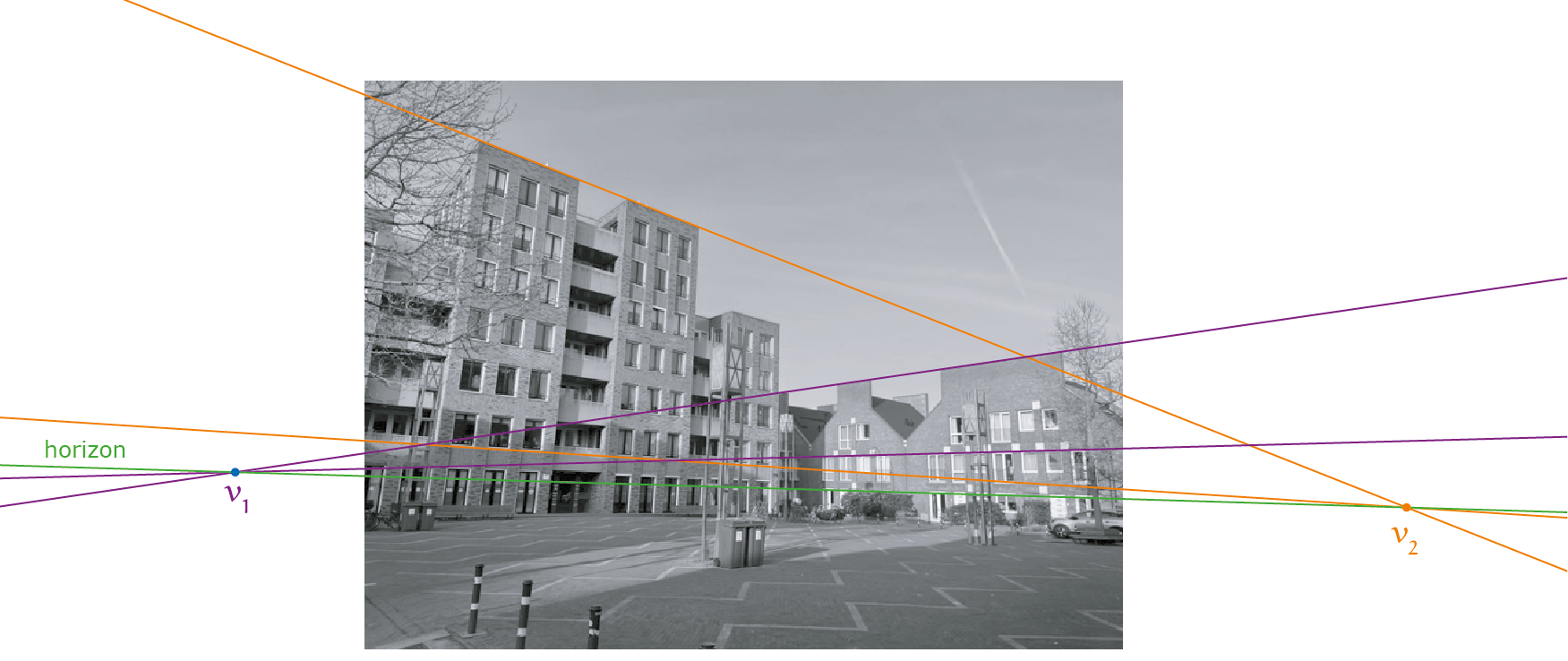
Lijnen parallel aan het beeldvlak vormen de uitzondering. Hun beelden zijn ook parallel. In figuur 2 zijn de verticale lijnen van de gevel op de foto ook parallel. In figuur 3 is dat niet zo, omdat de camera omhoog gericht is. Het vlak van de foto helt achterover en is dus niet parallel aan de gevel. De twee figuren 2 en 3 illustreren dat de beelden van parallelle lijnen parallel zijn of een gemeenschappelijk verdwijnpunt hebben (regel 2). In het speciale geval van horizontale lijnen ligt het verdwijnpunt op dezelfde hoogte als het gezichtspunt. Zoals parallelle lijnen hetzelfde verdwijnpunt hebben, zo hebben parallelle vlakken dezelfde verdwijnlijn. Van lijnen die onderling niet parallel zijn (en niet parallel aan het beeldvlak) maar wel in hetzelfde vlak liggen, liggen de bijbehorende verdwijnstralen in het vlak door $O$ parallel aan dat vlak. Daaruit kun je concluderen dat hun verdwijnpunten op één lijn liggen, de verdwijnlijn van dat vlak. Deze is ook de verdwijnlijn van alle andere vlakken parallel aan dat vlak (regel 3). De verdwijnlijn van alle horizontale vlakken ligt op ooghoogte en heet de horizon. Figuur 4 laat zien hoe je met een viertal lijnen op de foto (in $\color{orange}{oranje}$ en in $\color{purple}{paars}$) waarvan je weet dat ze in werkelijkheid horizontaal lopen, twee verdwijnpunten $V_1$ en $V_2$ kunt vinden die de horizon (in $\color{green}{groen}$) bepalen.

Verdwijnpunten en -lijnen op een afbeelding zijn niet terug te vinden in de werkelijkheid. In werkelijkheid snijden parallelle lijnen elkaar immers niet. De projectieve meetkunde is een meetkunde waarin ieder tweetal lijnen in een vlak elkaar snijdt. Het snijpunt van twee parallelle lijnen wordt verkregen door aan iedere lijn een 'punt in het oneindige' of een 'oneindig ver punt' toe te voegen, waarvan het verdwijnpunt het beeld is. Een verdwijnlijn is dan het beeld van een lijn van oneindig verre punten.

De dubbelverhouding

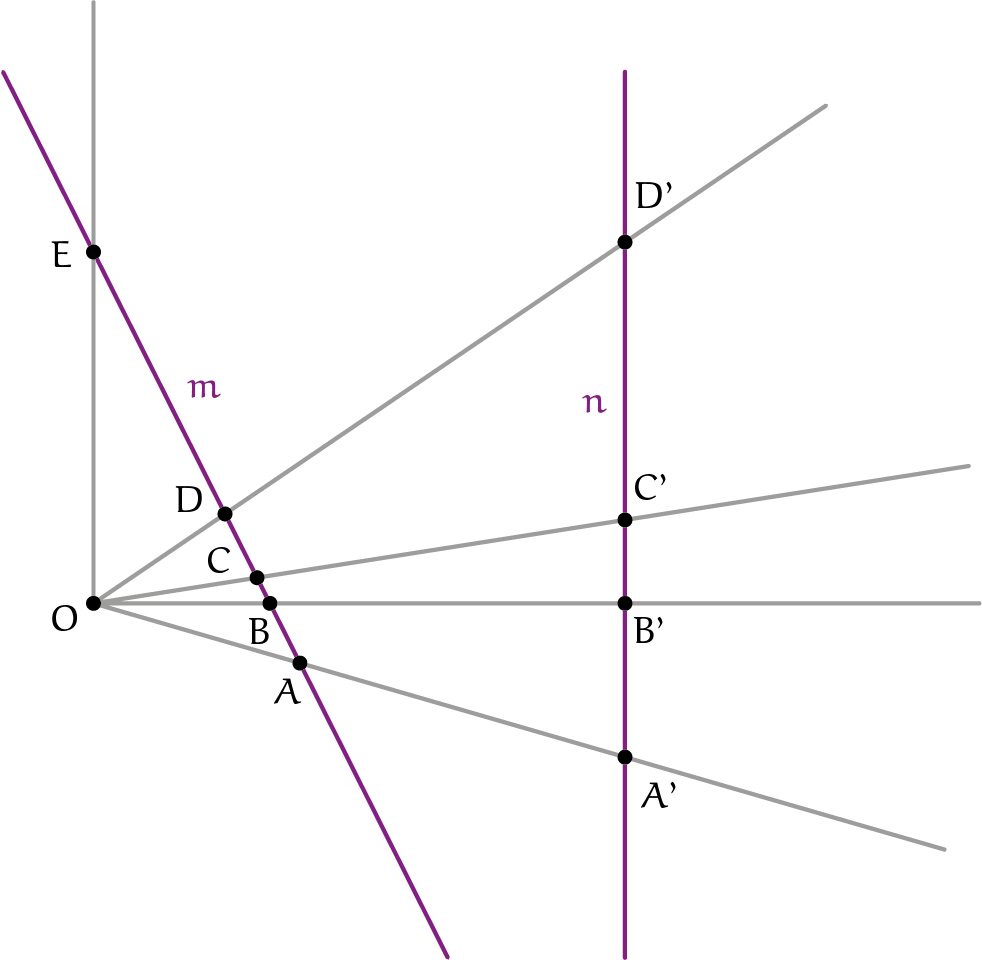
In de affiene meetkunde blijven de verhoudingen tussen de onderlinge afstanden tussen drie punten die op dezelfde lijn liggen behouden. Voor een projectie met centrum $O$ geldt dat duidelijk niet. Liggen punten in werkelijkheid op gelijke afstand van elkaar, dan liggen hun beelden naar het verdwijnpunt toe steeds dichter bij elkaar, zoals in figuur 1 te zien is. Verrassend genoeg is er een verhouding tussen de onderlinge afstanden tussen vier punten die op dezelfde lijn liggen die wel zijn waarde behoudt. De dubbelverhouding van vier punten $A$, $B$, $C$ en $D$ die in die volgorde op een lijn $m$ liggen (zie figuur 5), wordt gegeven door:

$$(A, B, C, D) = \frac{CA}{CB} \div \frac{DA}{DB} = \frac{CA \cdot DB}{CB \cdot DA},$$

waarbij $CA$ de afstand van $C$ tot $A$ is, enzovoort.

Een projectie met centrum $O$ beeldt deze punten af op de punten $A’$, $B’$, $C’$ en $D’$ op een lijn $n$. De opmerkelijke eigenschap van de dubbelverhouding is dat deze behouden blijft: $(A’, B’, C’, D’) = (A, B, C, D)$.

We bewijzen dit met vectoren, die we al zijn tegengekomen in de affiene meetkunde. Voor de vectoren van $O$ naar de verschillende punten geldt $\overrightarrow{OA'} = \alpha\overrightarrow{OA}$, $\overrightarrow{OB'} = \beta\overrightarrow{OB}$ en $\overrightarrow{OC'} = \gamma\overrightarrow{OC}$ voor zekere $\alpha$, $\beta$ en $\gamma$. Op de lijnen $m$ en $n$ geldt $\overrightarrow{CA} = \lambda\overrightarrow{CB}$ respectievelijk $\overrightarrow{C'A'} = \lambda'\overrightarrow{C'B'}$ voor zekere $\lambda$ en $\lambda'$.

Uit $\overrightarrow{OA}-\overrightarrow{OC}=\overrightarrow{CA}=\lambda\overrightarrow{CB}=\lambda\left(\overrightarrow{OB}-\overrightarrow{OC}\right)$ volgt $\overrightarrow{OA}=\lambda\overrightarrow{OB}+(1-\lambda) \overrightarrow{OC}$ en dus $\overrightarrow{OA'}=\alpha\overrightarrow{OA}=\alpha\lambda\overrightarrow{OB}+\alpha(1-\lambda)\overrightarrow{OC}$. Net zo geldt $\overrightarrow{OA'}-\overrightarrow{OC'}=\overrightarrow{C'A'}=\lambda'\overrightarrow{C'B'}=\lambda'\left(\overrightarrow{OB'}-\overrightarrow{OC'}\right)$ zodat ook $\overrightarrow{OA'}=\beta\lambda'\overrightarrow{OB}+\gamma(1-\lambda')\overrightarrow{OC}$.

Omdat $\overrightarrow{OB}$ en $\overrightarrow{OC}$ niet parallel zijn, zijn de coëfficiënten van $\overrightarrow{OB}$ in beide uitdrukkingen voor $\overrightarrow{OA'}$ gelijk: $\alpha\lambda=\beta\lambda'$. Er geldt dan voor het quotiënt van de verhouding tussen de gelijkgerichte vectoren $\overrightarrow{C'A'}$ en $\overrightarrow{C'B'}$ en de verhouding tussen de gelijkgerichte vectoren $\overrightarrow{CA}$ en $\overrightarrow{CB}$:

$$\frac{C'A'/C'B'}{CA/CB}=\frac{\lambda'}{\lambda}=\frac{\alpha}{\beta}.$$

Het valt op dat het rechterlid $\frac{\alpha}{\beta}$ niet afhangt van het punt $C$, zolang $C$ maar in lijn ligt met $A$ en $B$. Dus voor een ander punt $D$ op dezelfde lijn geldt 

$$\frac{D'A'/D'B'}{DA/DB}=\frac{C'A'/C'B'}{CA/CB}.$$

Herschikken van de breuken geeft 

$$\frac{C'A'\cdot D'B'}{C'B'\cdot D'A'}=\frac{CA\cdot DB}{CB\cdot DA},$$

ofwel $(A',B',C',D')=(A,B,C,D)$, de gelijkheid van de dubbelverhoudingen. (In deze afleiding komt naar voren dat de dubbelverhouding welbeschouwd bestaat uit verhoudingen tussen parallelle vectoren en dat strikt genomen het afstandsbegrip niet nodig is.)

De dubbelverhouding is ook toepasbaar wanneer er een punt in het oneindige meedoet: dan stellen we $(A, B, C, \infty) = CA/CB$. Als in figuur 5 $\overrightarrow{OE}$ parallel aan de lijn $n$ loopt, dan is $E$ in feite het verdwijnpunt van de projectie van de lijn $n$ op de lijn $m$ en is $(A, B, C, E) = (A’, B’, C’, \infty) = C’A’/C’B’$.

Een toepassing

We willen de hoogte bepalen van het gebouw in de figuren 2 en 3. We berekenen het hoogteverschil tussen een punt $P_0 = (X, Y, 0)$ op de grond tegen de gevel en het punt $P = (X, Y, Z)$ recht daarboven op de gezochte hoogte. Gegeven is een bekende referentiehoogte $Z_r$, met $0 \lt Z_r \lt Z$, van een punt $P_r = (X, Y, Z_r)$ tussen $P_0$ en $P$. De overeenkomende punten op de foto's zijn $p_0$, $p_r$ en $p$.

Opgave 1 Bepaal de hoogte van het gebouw met de foto in figuur 2 als gegeven is dat het punt $P_r$ op $2{,}4$ meter hoogte ligt.

Wanneer we slechts de foto in figuur 3 tot onze beschikking hebben, waarop hoogteverhoudingen niet werkelijkheidsgetrouw zijn, biedt de dubbelverhouding uitkomst. Daarmee kunnen we afstanden tussen punten op de foto gebruiken om afstanden tussen punten van het gebouw te bepalen. De dubbelverhouding werkt met vier punten die op een lijn liggen, dus er is nog een punt nodig. Dat kan het punt in het oneindige zijn. De dubbelverhouding $(P_0, P_r, P, \infty)$ heeft dezelfde waarde als de dubbelverhouding van de overeenkomende punten $p_0$, $p_r$ en $p$ op de foto en het verdwijnpunt $p_v$ dat buiten de foto valt:

$$(p_0, p_r, p, p_v) = (P_0, P_r, P, \infty) = \frac{PP_0}{PP_r}=\frac{Z}{Z-Z_r}.$$

Het linkerlid is uit rekenen door de afstanden tussen de punten $p_0$, $p_r$, $p$ en $p_v$ te meten en in te vullen in

$$(p_0, p_r, p, p_v) = \frac{pp_0\cdot p_vp_r}{pp_r\cdot p_vp_0}.$$

De gezochte hoogte volgt dan uit

$$Z=\frac{\left(p_0,p_r,p,p_v\right)}{\left(p_0,p_r,p,p_v \right)-1}Z_r.$$

 

Opgave 2 Bepaal de hoogte van het gebouw met figuur 3 als gegeven is dat het punt $P_r$ op $2{,}4$ meter hoogte ligt.

Als het goed is vind je (ongeveer) dezelfde uitkomsten in opgave 1 en opgave 2. Als de waarde van $(p_0, p_r, p, p_v)$ dichtbij 1 ligt is de formule behoorlijk gevoelig voor meetfouten of afrondingen, dus als de waarden niet helemaal overeenkomen kun je proberen te meten met meer precisie. Zoals gezegd zit de horizon op ooghoogte. Wanneer de horizon op de foto is te bepalen en de hoogte van de camera bekend is, dan kan die de referentiehoogte zijn. Als het camerastandpunt onbekend is, dan kan dat worden teruggerekend door de hoogte van de horizon te bepalen op basis van een bekende referentiehoogte. Deze technieken worden bijvoorbeeld gebruikt om niet meer bestaande gebouwen aan de hand van oude foto's (virtueel) te reconstrueren.

Opgave 3 Hoe kun je de hoogte $Z$ bepalen wanneer van zekere punten $P_1 = (X, Y, Z_{r1})$ en $P_2 = (X, Y, Z_{r2})$ met $0 \lt Z_{r1} \lt Z_{r2} \lt Z$ het hoogteverschil $Z_{r2} - Z_{r1}$ bekend is (dus wanneer er een verticale referentielengte bekend is die niet op de grond begint maar zich op een bepaalde hoogte bevindt)?

 

		VerwijzIngEn naAr het PythaGoras arChief Al in de tweede jaargang, Pythagoras 02-1/2/4/5, werd de projectieve meetkunde behandeld. Correct perspectieftekenen werd uitgelegd in Pythagoras 52-2/4/6, en fouten in oude prenten werden bestudeerd in Pythagoras 20-2. De klassieke stellingen van de projectieve meetkunde zijn uitspraken over de onderlinge ligging van punten en lijnen, zoals de stelling van Pappus en de stelling van Desargues, Pythagoras 20-3/4/5.