We bekijken de wedstrijd tussen twee spelers die met dezelfde munt gooien. We gaan er vanuit dat beiden een sterke keuze hebben gemaakt, bijvoorbeeld KMM en MMK. Een gevolg van het gooien met één munt, is dat nu een ‘misser’ bij de een kan leiden tot een bruikbare tussenstand voor de tegenstander.

Om de wedstrijd goed in beeld te krijgen maken we net als in de eerste twee afleveringen weer gebruik van Markov ketens in figuur 1.

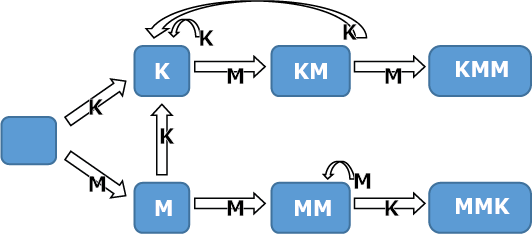
Het bovenste gedeelte geeft de tussenstanden op weg naar KMM weer, het onderste deel laat de route naar MMK zien.

In het diagram is goed te zien dat bij de tussenstand K het pleit is beslecht in het voordeel van KMM. Als dat tussenstation eenmaal is bereikt, is er geen route naar MMK meer mogelijk. De kans om vanuit de start tussenstand K te bereiken is makkelijk te berekenen: er zijn slechts twee routes van het begin naar K, één direct, en één via M:

$$P({\rm K})=\frac{1}{2}+\frac{1}{2}\times\frac{1}{2}=\frac{3}{4}.$$

Daarmee ligt de winstkans dus vast.

Nog korter is de berekening van de kans dat MM wordt bereikt (nodig en voldoende voor een overwinning van MMK). Deze is gelijk is aan $\frac{1}{2}\times\frac{1}{2} = \frac{1}{4}.$ De winstverhouding is dus 3 : 1 in het voordeel van KMM. Wanneer KMM het moet opnemen tegen KKM krijgen we een heel ander beeld. Omdat de eerste worp van beide reeksen gelijk is hoeven we niet meteen te splitsen. De bijbehorende Markov keten staat in figuur 2.

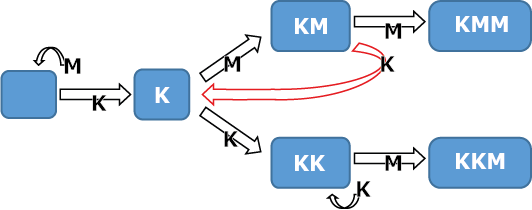
Ook hier zijn de kansen goed te berekenen. Omdat beide reeksen beginnen met een K begint de wedstrijd eigenlijk pas nadat de eerste K is geworpen. De wedstrijd is beslist (in het voordeel van KKM) wanneer KK is bereikt. Dit kan direct, maar ook via een of meer ‘rondjes’ via KM-K:

$$P({\rm KK}) = \frac{1}{2} + \left(\frac{1}{2}\right)^3 + \left(\frac{1}{2}\right)^5 + \left(\frac{1}{2}\right)^7 + \cdots =\frac{1}{2}\cdot\frac{1}{1 - \frac{1}{4}} = \frac{2}{3}.$$

Op een soortgelijke manier kan P(KMM) berekend worden, maar we kunnen al concluderen dat deze gelijk zal zijn aan $\frac13.$

Het lijkt er op dat KKM nog sterker is dan KMM, baas boven baas: $\begin{matrix}{\rm KKM}\\{\rm KMM}\\{\rm MMK.}\end{matrix}$

Opmerkelijk genoeg blijkt MMK goed opgewassen te zijn tegen zijn ‘tegenvoeter’ KKM, maar het wordt nog vreemder: KKM wordt twee van de drie keer verslagen door MKK . Als je in het eerste diagram alle M’s door K’s verwisselt, zie je waarom.

Bij de vier sterke patronen (KMM, MMK, MKK en KKM) is het geen kwestie van baas boven baas, maar een kringetje, waarbij ieder patroon een opponent heeft die meestal wordt verslagen, én een waarvan meestal wordt verloren.  Voor wie het spel “papier, schaar, steen” kent, komt dit wellicht enigszins bekend voor. In figuur 3 is de kringloop goed te zien.

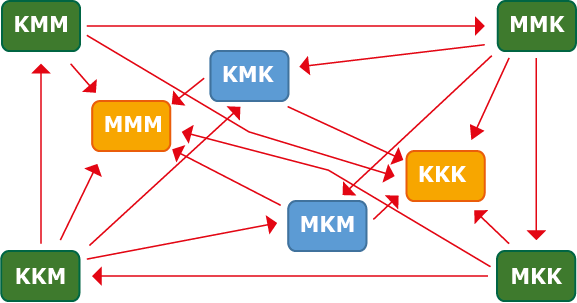
Voor de volledigheid zijn ook andere, minder sterke patronen opgenomen. Dat KKK meestal verliest van MKK zal geen verrassing zijn, maar misschien wel dat dit 7 van de 8 keer gebeurt. Toch is dit zelfs zonder diagram in te zien. KKK kan alleen winnen als er direct drie keer achter elkaar KKK wordt geworpen. Zodra er een M wordt geworpen is KKK kansloos, er zal immers altijd eerder MKK worden gegooid dan MKKK.

Deze gedachtegang kan leiden tot een strategie waarmee je altijd kunt winnen van iemand die zijn patroon heeft verteld:

1. Kopieer het patroon met uitzondering van de laatste worp
2. Zet het tegengestelde van de tweede worp ervoor

Als iemand KKM kiest, kun je dus met MKK vaker winnen, en KMMKK kan succesvol worden bestreden met KKMMK. Als iemand zo vriendelijk is om voor KKKKK te kiezen, is uiteraard MKKKK het juiste antwoord. Je winstkansen zijn dan erg groot. Je tegenstander heeft maar een kans van $(\frac{1}{2})^5 = \frac{1}{32}$ om te winnen.

Bij een wedstrijd tussen bijv. MKKKK tegen KMKMK zijn de winstkansen wat lastiger te bepalen. We kijken in figuur 4 eerst naar de bijbehorende Markovketens.

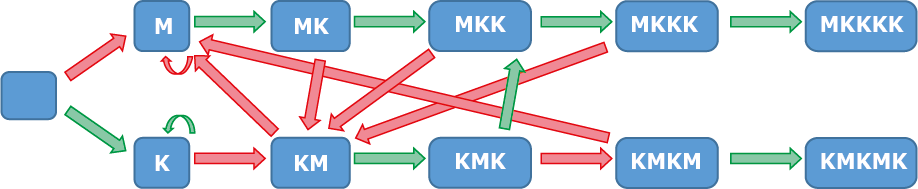
De rode pijlen geven aan dat er Munt wordt gegooid, de groene betekenen Kop. Uiteraard zijn de bijbehorende overgangskansen steeds $\tfrac{1}{2}.$ We kunnen alle overgangskansen in een matrix zetten en kijken wat op de lange duur het resultaat is, maar met wat vergelijkingen zijn de winstkansen ook handmatig te bepalen. We gaan daarbij uit van de stationaire verdeling die als limietgeval optreedt. We gebruiken de letters $a, b, c, d, e$ als maat voor de waarschijnlijkheid dat respectievelijk M, MK, MKK, MKKK en MKKKK worden bereikt, $p, q, r, s, t$ voor de tussenstanden in de onderste reeks. Dit geeft:

1. $a = (1 + a + q + s)/2 \leftrightarrow 2a = a + q + s + 1 \leftrightarrow a = q + s + 1$ [M]
2. $b = a/2 \leftrightarrow  a = 2b$ [MK]
3. $c = (b + r)/2 \leftrightarrow  b + r = 2c \leftrightarrow b = 2c ‒ r$ [MKK]
4. $d = c/2 \leftrightarrow  c = 2d$ [MKKK]
5. $e = d/2 \leftrightarrow  d = 2e$ [MKKKK]
6. $p = (1 + p)/2 \leftrightarrow 2p = p+1 \leftrightarrow p = 1$ [K]
7. $q = (p + b + c + d)/2 \leftrightarrow 2q = p + b + c + d$ [KM]
8. $r = q/2 \leftrightarrow  q = 2r$ [KMK]
9. $s = r/2 ↔ r = 2s$ [KMKM]
10. $t = s/2 ↔ s = 2t$ [KMKMK]

Combinatie van 1, 8, 9 en 10 geeft $a = 8t + 2t + 1  \leftrightarrow a = 10t + 1.$ [$\star$]

Uit 2 en 3 volgt $a = 4c ‒ 2r.$ In combinatie met 4, 5, 8, 9 en 10 leidt dit tot $a = 16e ‒ 8t.$ [$\dagger$]

Uit [$\star$] en [$\dagger$] volgt: $16e ‒ 8t = 10t + 1 \leftrightarrow 16e = 18t + 1.$ [$\S$]

Combineren van 7 t/m 10 geeft: $16t = 1 + (2c ‒ r) + c + d = 1 + 8e ‒ 4t + 6e \leftrightarrow 20t = 14e + 1.$ [$\Omega$]

We herschrijven [$\S$] en [$\Omega$] als: $16e ‒ 18t =1$ en $-14e + 20t = 1.$

Hieruit volgt $16e ‒ 18t = -14e + 20t \leftrightarrow 30e = 38t \leftrightarrow e : t = 38 : 30 = 19 : 15.$

Herinner je dat $e$ de kans is op MKKKK en $t$ de kans op KMKMK. Het kiezen voor MKKKK is dus iets beter dan de keuze voor KMKMK. De winstkans bij de juiste keuze is 19/34 (≈ 56%).

De beroemde wiskundige John Conway bedacht een snellere methode, die mogelijk wel wat gewenning vraagt. Deze methode werkt met overlap. We letten eerst op de overlap van het einde van de reeks MKKKK met het begin van KMKMK.

Er is in dit geval een overlap van lengte 1 : MKKKKMKMK.

Als we de twee reeksen verwisselen van plaats is er een grotere overlap: KMKMKKKK.

Er wordt ook gekeken naar overlap van een reeks met zichzelf. Bij MKKKK kan dat maar op één, vrij triviale manier MKKKK, maar bij KMKMK zijn er meer mogelijkheden: KMKMK, KMKMKMK en KMKMKMKMK.

In zijn algoritme kent Conway aan elke mogelijke overlapping de waarde $2^{L-1} toe, met $L$ de lengte van de overlapping. Als er meerdere overlappingen zijn worden de waarden opgeteld. Met een klein beetje rekenen (in feite het omzetten van binaire getallen in decimale notatie) krijgen we:

• MKKKK - KMKMK  : $2^{1-1} = 2^0 =1$
• KMKMK - MKKKK  : $2^{2-1}=2^1=2$
• MKKKK - MKKKK   : $2^{5-1} = 2^4 =16$
• KMKMK - KMKMK  : $2^4 + 2^2 +2^0 = 21$

De kansverhouding MKKKK : KMKMK is nu $(21 ‒ 2) : (16 - 1) = 19 : 15,$ en dat klopt met de uitkomst hierboven.