
De negenpuntscirkel van Feuerbach
In een willekeurige driehoek liggen de drie middens van de zijden, de drie voetpunten van de hoogtelijnen en de middens van de lijnstukken die de hoekpunten van de driehoek verbinden met het hoogtepunt op één cirkel.
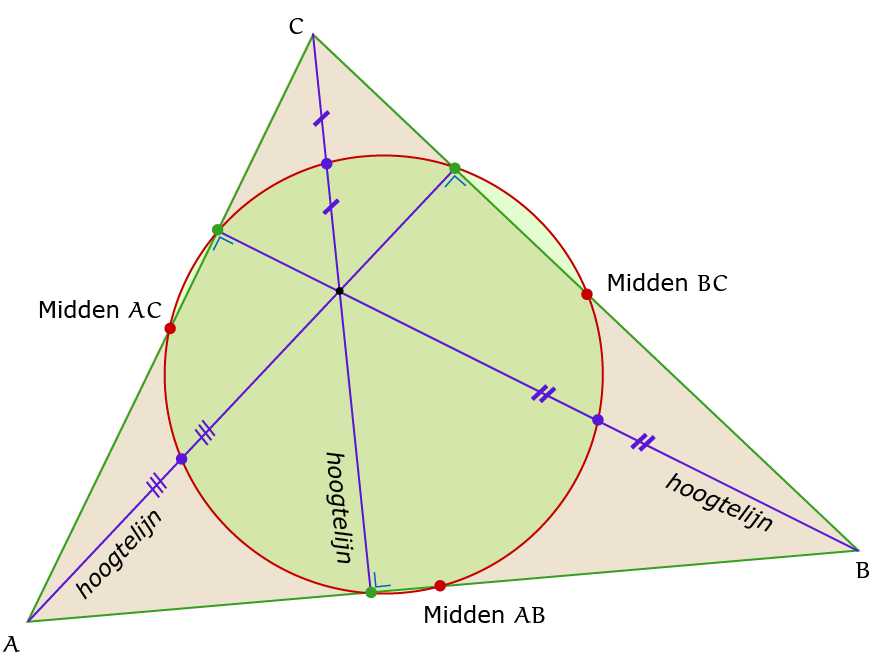
In 1765 bewees Leonhard Euler dat in een willekeurige driehoek de drie middens van de zijden (rode punten in de figuur) en de drie voetpunten van de hoogtelijnen (groene punten) alle zes op een cirkel liggen. In een artikel uit 1821 van Charles Brianchon en Jean-Victor Poncelet werd de aandacht gevestigd op het feit dat er nog drie andere punten op diezelfde cirkel liggen, namelijk de middens van de lijnstukken die de hoekpunten van de gegeven driehoek verbinden met het hoogtepunt (blauwe punten). Het eerste volledige bewijs, door Karl Feuerbach, dateert uit 1822. De naam negenpuntscirkel verschijnt in 1842 voor het eerst in druk.
| Feuerbach | Poncelet | Pascal | Morley | Torricelli | Ceva |
