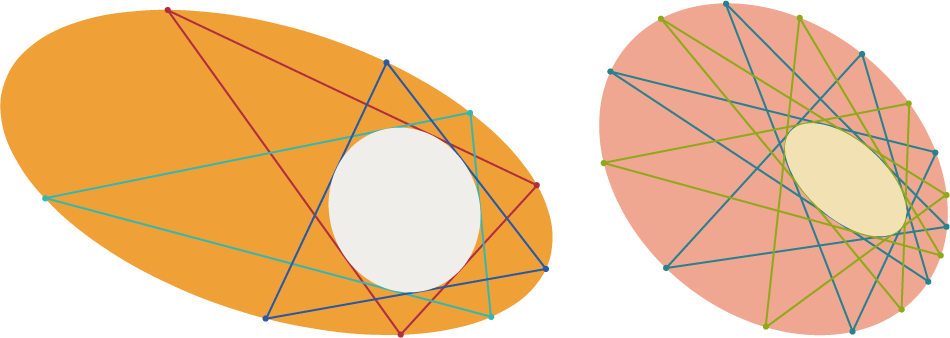
Een eenvoudig geval van deze stelling zegt het volgende. Gegeven twee ellipsen die in elkaar liggen, zoals in de figuren. Neem een punt op de buitenste ellips en een rechte door dat punt die raakt aan de binnenste ellips. Deze rechte snijdt de buitenste ellips in een welbepaald punt. Met dat punt werken we verder zoals met het eerst gekozen punt: de (andere) raaklijn door dat punt aan de binnenste ellips snijdt de buitenste ellips in een volgend punt. We herhalen dit procedé. Als we op een bepaald ogenblik terug uitkomen bij het eerst gekozen punt, en als dat gebeurt na $n$ stappen in het proces, dan zal dit steeds het geval zijn: met welk punt op de buitenste ellips we ook starten, in $n$ stappen zijn we terug bij het beginpunt. In de linker figuur zie je twee ellipsen waar dat in $3$ stappen het geval is, in de rechter figuur zijn er $8$ nodig.

Jean-Victor Poncelet bewees deze stelling een eerste keer in 1813, in een gevangenis in Rusland. Poncelet was luitenant in het leger van Napoleon, en bij de veldtocht van deze laatste naar Rusland werd hij gevangengenomen bij de slag van Krasnoi. In de gevangenis ontwikkelde hij de projectieve meetkunde.

Een porisme is in essentie een stelling die volgt uit een andere. Tegenwoordig wordt deze benaming enkel nog gebruikt bij gevallen zoals bovenstaande: als er voldaan is aan een zekere voorwaarde, dan is de eigenschap in kwestie waar in oneindig veel gevallen.

 

Feuerbach | Poncelet | Pascal | Morley | Torricelli | Ceva