
De stelling van Pascal
In een willekeurige zeshoek $ABCDEF$ met hoekpunten op een kegelsnede liggen de snijpunten van de overstaande zijden $AB$ en $DE$, $BC$ en $EF$, $CD$ en $FA$ op een rechte lijn.
In 1640 schreef Blaise Pascal dat van een willekeurige zeshoek $ABCDEF$ met hoekpunten op een kegelsnede, de snijpunten van de overstaande zijden $AB$ en $DE, BC$ en $EF, CD$ en $FA$ op een rechte lijn liggen.
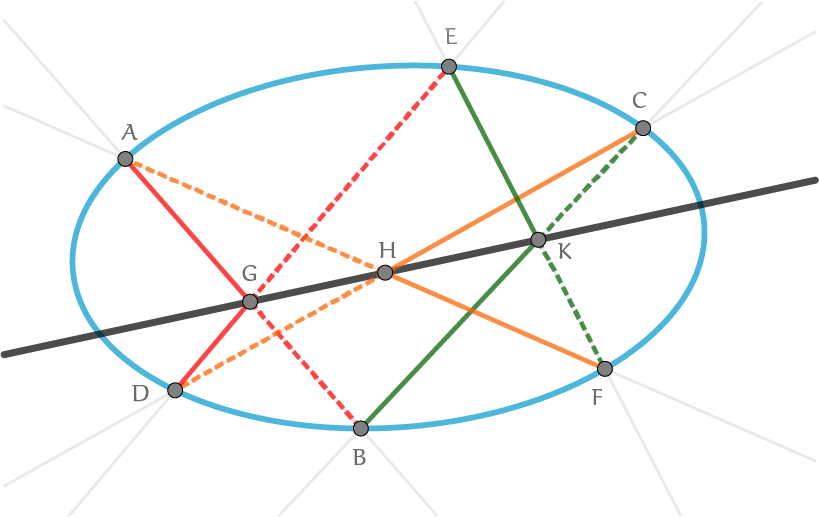
Pascal gaf geen bewijs. Later is deze stelling op verschillende manieren, meetkundig en algebraïsch, bewezen en ook gegeneraliseerd. Hier staat de stelling afgebeeld voor een ellips en voor een hyperbool.
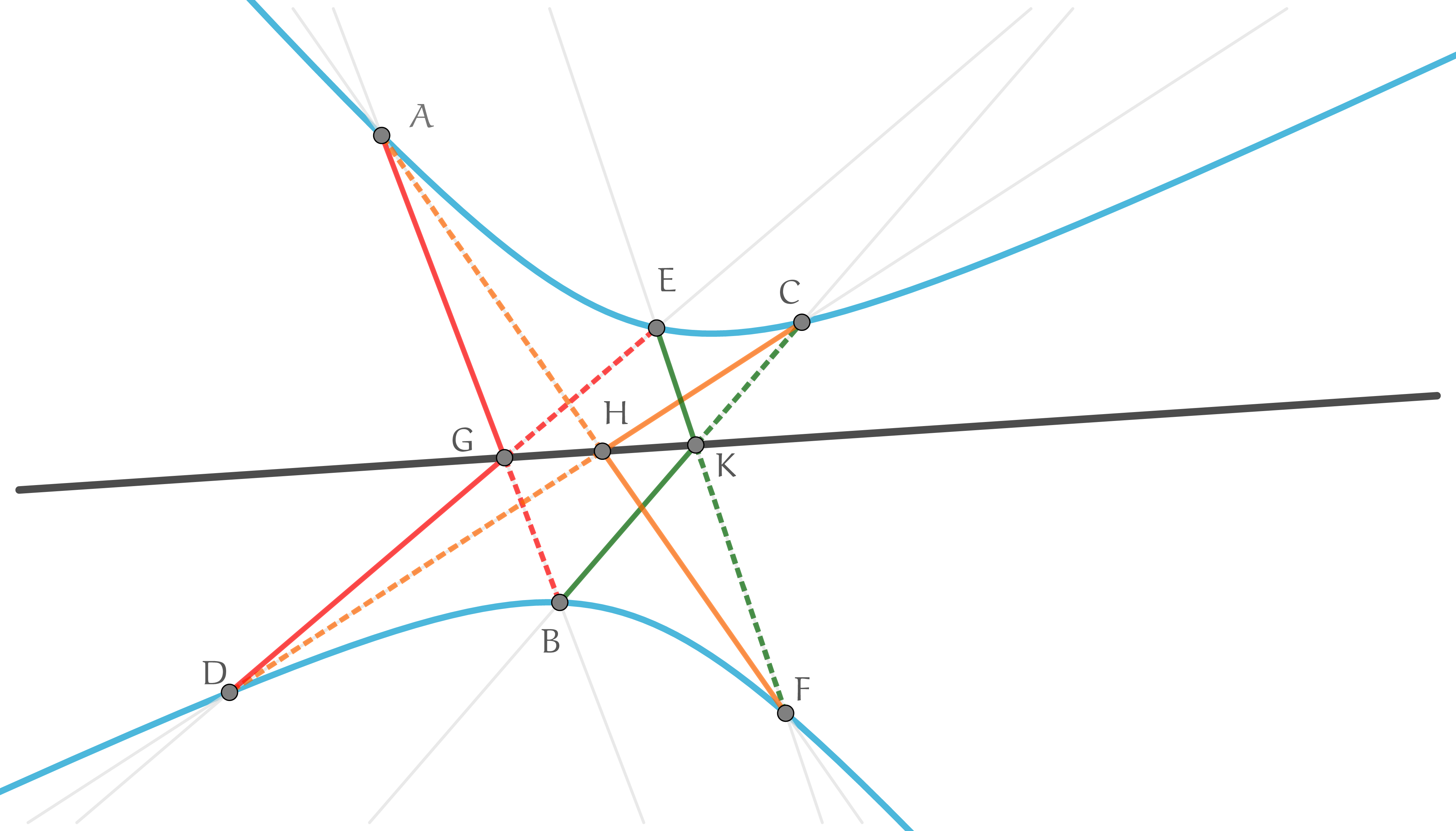
Op 3 januari 2014 plaatste Dao Thanh Oai de volgende eigenschap op de Cut the Knot-Facebookpagina. Als je de zeshoek doorloopt dan geldt voor de lijnstukken $AG$ tot en met $HA{:}$
$$\frac{AG}{GB} \cdot \frac{BK}{KC}\cdot \frac{CH}{HD}\cdot \frac{DG}{GE}\cdot \frac{EK}{KF}\cdot \frac{FH}{HA} = 1$$
Het schijnt dat hij de eigenschap heeft ontdekt door te experimenteren met Geogebra. De Facebook-pagina bestaat helaas niet meer. Deze is verder gegaan als Interactive Mathematics Miscellany and Puzzles.
Op de bijbehorende website Cut the Knot is een bewijs te vinden.
| Feuerbach | Poncelet | Pascal | Morley | Torricelli | Ceva |
